Об оценивании времени работы управляющего фондом акций

эмпирическую дисперсию

n ₂

² 2 =1 £ ( h , — h " )

n =1

и нормализованный размах накопленных сумм H k

P

n

n

n

В предположении независимости и одинаковой распределенности величин h 1 ,h 2 ,... распределение Θ n не зависит от среднего значения и дисперсии величин h k при k ≤ n. Последнее дает возможность проверять гипотезу о том, что рассматриваемые значения индекса или пая подчиняются схеме случайного блуждания.

P ^   1.

ln 0 =ln — n ~ lnJ — + — In n n 2 n 2   2

Таким образом, в логарифмической шкале значения ln Θ n должны лежать ря- n ,1

дом с прямой lnJ — + — ln n , откуда возникает следующий подход для анализа индекса.

Вычисляем значения Θ n и наносим точки (ln n ; ln Θ n ) на плоскость с соответствующими логарифмическими шкалами. С помощью метода наименьших квадратов находим прямую a^{^} + b^{^} ln n . Угловой коэффициент прямой называется коэффициентом Харста и обозначается H.

Если b^{^} будет значимо отличаться от 0.5, то гипотезу о случайном блуждании следует отвергнуть.

Таким образом, R/S-анализ позволяет сравнивать рискованность того или иного фонда. При стремлении коэффициента Харста к 1 шумовая компонента процесса становится меньше. При H = 1 имеем дело со стандартным фрактальным броуновским движением B 1 (t) = tξ, где ξ : N (0;1), которое наименее «зашумленное» в классе всех фрактальных броуновских движений с параметром 0 ˂ H ≤ 1. Поэтому и модели, описываемые такими процессами, являются менее рискованными.

Возвращаясь к проблеме оценки качества управления фондом, а точнее, к проблеме определения момента времени, когда по показателям фонда можно делать надежные выводы о его управляющем, исследуем поведение коэффициента Харста (табл. 4-9; рис. 1-2) .

Из результатов анализа индекса ММВБ (см. табл. 6) мы видим, что коэффициент Харста оказался значительно больше 0.5. Причина, по всей видимости, заключается в том, что мы имеем дело с системой с долгой памятью, говорят, что сохраняется тенденция движения (например, если

Таблица 4. Коэффициент Харста для индекса ММВБ в период с 01.2005 по 06.2006

Квартал K	K 1	K 2	K 3	K 4	K 5	K 6
Длительность наблюдений в месяцах	3	6	9	12	15	18
Коэффициент Харста H	0,3768	0,4552	0,5071	0,4829	0,4999	0,5018

Таблица 5. Коэффициент Харста для индекса ММВБ в период с 07.2006 по 12.2007

Квартал K	K 7	K 8	K 9	K 10	K 11	K 12
Длительность наблюдений в месяцах	21	24	27	30	33	36
Коэффициент Харста H	0,5164	0,5249	0,5327	0,5497	0,5677	0,5804

Таблица 6. Коэффициент Харста для индекса ММВБ в период с 01.2008 по 05.2012

Месяцы	42	48	54	60	66	72	78	84	90
H	0,6082	0,6306	0,6493	0,6542	0,649	0,6377	0,6285	0,6251	0,6258

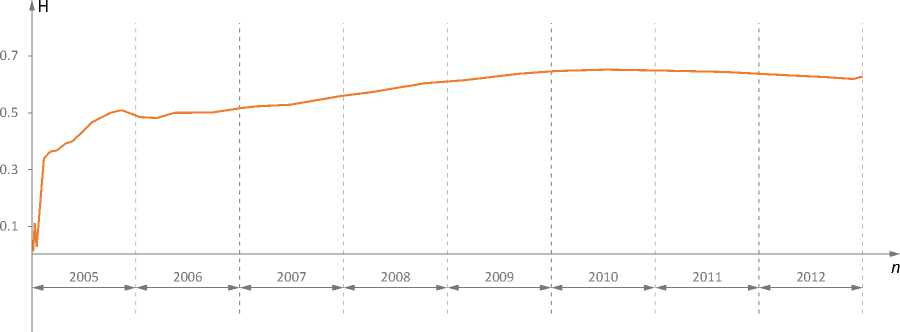
Рис. 1. Индекс ММВБ: 2005 – 2012 гг.

наблюдается рост, то с большой вероятностью он будет продолжаться). Таким образом, приходим к выводу, что менее рискованно иметь дело с ценными бумагами, основанными на индексе ММВБ, нежели с акциями компаний. Это легко объясняется диверсификацией, которая свойственна индексу ММВБ. Но, как уже было ранее указано, при оценке деятельности управляющего опираться на показатели риска не представляется разумным, для больших H возможны продолжительные спады, что не противоречит меньшему риску. Напротив, при меньшем шуме проявляется большая настойчивость в сохранении направления движения.

Проводя аналогичные вычисления для инвестиционного фонда, в первую очередь следует отметить некоторое пре- восходство параметра фрактальности для фонда над тем же показателем для индекса ММВБ. Это, по всей видимости, объясняется тем фактом, что при схожей структуре индекса и паевого фонда последний является более надежным, поскольку, как указывалось ранее, часть денежных средств остается на счетах фонда.

Из приведенных таблиц видно, что изменение коэффициента Харста для фонда не превышает 0,02 в течение полугода, начиная с 21 месяца, а стабилизация происходит около значения 0,6. Начиная со второй половины 2006 года и до середины 2012 года коэффициент Харста находится в пределах от 0,55 до 0,654. Поэтому

Таблица 7. Коэффициент Харста для фонда 1 в период с 01.2005 по 06.2006

Инвестиционный фонд 1 01.2005 – 06.2006
Квартал K	K 1	K 2	K 3	K 4	K 5	K 6
Длительность наблюдений в месяцах	3	6	9	12	15	18
Коэффициент Харста H	0,5022	0,5438	0,5882	0,5575	0,5357	0,5367

Таблица 8. Коэффициент Харста для фонда 1 в период с 07.2006 по 12.2007

Инвестиционный фонд 1 07.2006 – 12.2007
Квартал K	K 7	K 8	K 9	K 10	K 11	K 12
Длительность наблюдений в месяцах	21	24	27	30	33	36
Коэффициент Харста H	0,5559	0,568	0,5751	0,5871	0,5978	0,6035

Таблица 9. Коэффициент Харста для фонда 1 в период с 01.2008 по 05.2012

Инвестиционный фонд 1 01.2008 – 05.2012
Месяцы	42	48	54	60	66	72	78	84	90
H	0,6124	0,6278	0,6497	0,6576	0,6537	0,6477	0,6349	0,6275	0,6302

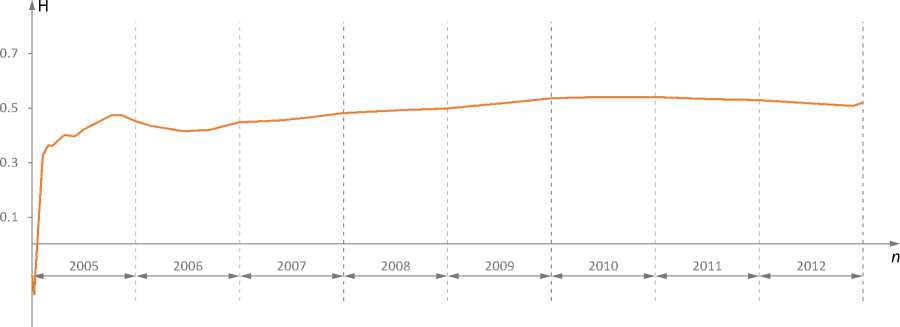
Рис. 2. Инвестиционный фонд 1: 2005 – 2012 гг.

к концу второго года можно делать обоснованные выводы о качестве управляющего, при этом отметим, что делать это должно руководство компании, опираясь на различные показатели и собственное видение ситуации, мы же только указываем срок, по истечении которого они могут быть достаточно надежными.

Метод 3: Мартингальный подход

Здесь мы попытаемся оценить время, необходимое для оценки качества работы управляющего, используя широко распространенный мартингальный подход. Основой предлагаемого метода служит пример, представленный в книге А.Н. Ширяева [7] (глава II, §5). Ввиду лако- ничности изложения, мы позволим себе более подробное описание с некоторыми уточнениями.

Рассмотрим модель, в которой относительное приращение индекса X n , n = 0,1,... определяется рекуррентными соотношениями

X n+1 = 0 • X n + (1 - 0) • ^ n+1 , n > 0, (2)

где величина θ∊R является неизвестным параметром. Случайные величины Xo,^i,^2,..., определенные на некотором вероятностном пространстве (Ω, Φ, Ρ), считаются невырожденными, независимыми и квадратично интегрируемыми, а математическое ожидание всех инно- ваций ξn– равным нулю. Отметим, что множитель (1 – θ), расположенный в правой части (2) является излишним и участвует в равенстве, обеспечивая сходство с применяемой на практике EWMA моделью (описание модели см., например, у А.Н. Ширяева [7]).

Принимая каждое из значений X0, X1, ... как результат наблюдений, рассмотрим в качестве оценки параметра θ величину n-1

E X k ^X k +1

9 n = k = n 1 k + + ¹  , D k = Df ), k ^€ N , (3)

EXk k=0 Dk+1

n mn = I(-k - E(Mk |F,-)), An = k=1

n

= I ( E ( - k ²|F . - ) - - L).

k =1

Компенсатор A n перепишем в виде

n

An = IE(-k - Mk2_JFk-- Mp) = k=1

n

= I E (( - k - - k Vl F k - ) =

k =1

n

= IE k=1

(r 2

He-16'

(V D k 7

I ^F k -,

полагая ее равной нулю, в случае если знаменатель дроби обращается в ноль. В дальнейшем мы будем предполагать, что выполнено условие Ρ{ω : X0(w)=0}=0, гаранти- n —1 X 2

рующее P-п.н. неравенство ^—— = 0 .

k =0 D k +1

Используя равенство (2), мы представим (P-п.н.) оценку θ n в виде

n Y ²

Z X k -1

k =1 D k

E (S\F k - ) = I

n X

- 2

k -1

.

k =1

D k

Последнее равенство означает, что M предложенная оценка 9_n = 9 +-- n .

n        An

Так как

A= E ( M 1 | F 0)= E ( X²f ²)= E ( X 0²) ■ E f ²) = 0,

M

0n = 9 + (1 - 9) -n, An n-1 у e             n-1 у 2

-n = I . An = I XT к=0 Dk+1           k=0 Dk+1

M то для P-п.н. сходимости —n ^ 0., n^^, An эквивалентной P-п.н. сходимости θn→θ, n→∞, достаточно двух условий5

.

sup X+L < M.

n D nn

( f f

I ^E min n =1 l    v D-

M

n

= m . (4)

Стохастическая последовательность (M n ,F n ) n≥1 с фильтрацией Φ = σ(X 0 ,ξ 1 , ... ξ n ) образует мартингал, поскольку

(n - 2 у e

E ( - . | F . )   I - f ¹

V k =0 D k + 1

+ - n - 1 f n

D n

| ^F n - 1

Возвращаясь к оценке эффективности управляющего, мы рассмотрим для относительных приращений величины пая модель (2), в которой случайные величины ξ 1 ,ξ 2 ,... имеют одинаковое распределение. В этом случае условия (4) выполне-

n - 2

= I P ' + -P² E f. I F.) = M , ..

k =0 D k + 1      D n

( n -1

ны и оценка 9 _n = I I X , X k „

V k =0

n -1

И I X'k

V k =0    7

схо-

В последнем равенстве мы использовали независимость X 0 ,ξ 1 , ... ξ n и равенство Eξ n = 0 . Определив Φ 0 = { ∅ ,Ω}, M 0 = 0, рассмотрим разложение Дуба [2] для субмартингала (M² n ,F n ) n≥1 :

дится P-п.н. к неизвестному параметру θ . Для проверки применимости модели (2) к исследуемому фонду обратимся к графикам изменения оценок θ n в периоды 2005 – 2006 гг. и 2005 – 2012 гг. (рис. 3, 4).

⁵ Для строгого доказательства необходимо усилить условие A 1 ≥ 1 P-п.н. теоремы 4 до A 1 > 0 P-п.н. и условие a n > 0, n ∊N задачи 6 до a 1 > 0, a n ≥ 0 при n ≥ 2.

0.5

0.4

0.3

0.2

0.1

Рис. 3. Изменение оценки в период 2005 – 2006 гг.

1   5    9   13   17   21   25   29   33   37  41   45   49   53   57   61   65   69 73   77   81  85   89   93   97 101

0.5

0.4

0.3

0.2

0.1

1   14 27 40 53 66 79 92 105 118 131 144 157 170 183 196 209 222 235 248 261 274 287 300 313 326 339 352 365 378

Рис. 4. Изменение оценки в период 2005 – 2012 гг.

На представленных графиках мы видим, что сходимость θ n имеет место. Более того, в конце 2008 года наблюдается характерный всплеск, обусловленный общей нестабильностью рынка, который впоследствии нивелируется. Данный эффект можно интерпретировать как устойчивость используемой модели, что вместе со сходимостью θ n оправдывает ее применение.

Оцениваемый параметр θ определяет зависимость будущей прибыли X n+1 от предыдущего наблюдения X n и инновации ξ n+1 , поэтому может выступать характеристикой риска. Таким образом, оценка эффективности управляющего может основываться на величине θ n при условии ее близости к истинному значению параметра. При этом время, необходимое для качественной оценки, будет определяться скоростью сходимости θ n .

Для исследования скорости сходимости рассмотрим период 2005 – 2007 гг.

Последнее значение оценки θ n , равное 0,0889, мы примем за истинное значение θ и для каждого из 12 кварталов этого периода K j вычислим величину

A j = max | в _п - У |, j = 1, _ ,12.

n ∈ K _j

Соответствующие таблицы 10, 11 .

Мы видим, что приемлемая точность оценки θ n (в смысле сходимости к θ ) появляется лишь после 18 – 21 месяцев наблюдений, что согласуется с полученными ранее результатами. Отметим здесь также, что данные по другим фондам приводят к аналогичным цифрам и говорят о необходимости по крайней мере 18 месяцев наблюдений (соответствующий график см. в следующем разделе).

Предложенная модель (2) позволяет инвесторам сравнивать различные фонды по оценкам θ n . Интересно отметить, что оценки параметра θ , вычисленные для индекса ММВБ не могут служить

Таблица 10. Динамика величины Δ в период 01.2005 – 06.2006

Квартал K	K 1	K 2	K 3	K 4	K 5	K 6
Длительность наблюдений (мес.)	3	6	9	12	15	18
Величина Δ	0,3570	0,0570	0,1929	0,1773	0,1828	0,1447

Таблица 11. Динамика величины Δ в период 07.2006 – 12.2007

Квартал K	K 7	K 8	K 9	K 10	K 11	K 12
Длительность наблюдений (мес.)	21	24	27	30	33	36
Величина Δ	0,0405	0,0169	0,0159	0,0147	0,0164	0,0037

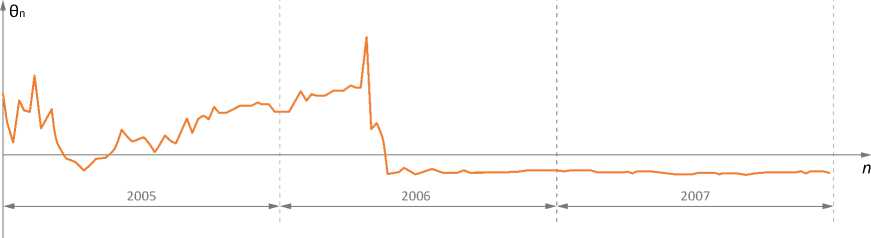
Рис. 5. Динамика оценки параметра для индекса ММВБ в период 2005 – 2007 гг.

в данном случае бенчмарком. Действительно, если обратиться к графику последовательности θ n , соответствующей индексу ММВБ, мы увидим следующую картину (рис. 5).

На графике видно, что с ростом n оценочное значение θ n становится отрицательным и, следовательно, не может интерпретироваться как мера риска. Ниже мы предложим один из способов построения такого бенчмарка, который может оказаться полезным и в других целях.

Построениеуниверсального индекса

Как уже отмечалось выше, оценка деятельности управляющего в большинстве случаев выражается в сравнении характеристик его фонда (среднего, дисперсии, коэффициента Шарпа) с соответствующими показателями некоторого универсального индекса. До настоящего момента в работе предполагалось, что универсальным является индекс ММВБ. Однако в некоторых случаях более корректным является построение такого индекса, например, на основе стоимости паев крупнейших индексных фондов.

Самым распространенным способом построения универсального показателя по-прежнему остается вычисление среднего арифметического некоторых выбранных величин, что объясняется простотой данной методики и многими замечательными свойствами. Ниже мы предложим усовершенствованный метод расчета, в котором среднее арифметическое заменяется взвешенной суммой. При этом веса выбираются таким образом, чтобы получившийся показатель имел наибольшую корреляцию с ММВБ. Преимущество этого метода заключаются в следующем. Далеко не все индексные фонды точно повторяют структуру индекса (особенно часто это встречается у фондов небольшого размера). У крупных фондов есть другая особенность: из-за своей популярности они часто встречаются с активными вводами/выводами денежных средств, что приводит к необ- ходимости регулярно осуществлять операции, что негативно сказывается на доходности. Вес таких фондов в нашем взвешенном индексе будет минимальна.

Для формулировки поставленной задачи на математическом языке нам потребуются следующие обозначения. Пусть v и i v - векторы пространства R n , а ∑ – строго положительно определенная матрица. Под выражениями || v || и || v | z мы будем понимать нормы в Rⁿ, порожденные соответственно скалярными произведениями

(V,w) = VT • w = £vw к=1

n и (v,w)Z = v T Z w = ^vi^jjWj.

i , ^j =1

Используя данные обозначения, сформулируем задачу построения универсального показателя.

Пусть ^1,^2,..., ^п,П — невырожденные случайные величины, отвечающие значениям стоимости паев выбранных индексных фондов Ki, K2, ..., Kn и значению индекса ММВБ соответственно. Тогда сформулированная выше задача сводится к нахождению вектора а = (а* а2,..., аП), такого, что а* = arg max |сог(аг + а2^2 + ... + ап^п,п)].

S eR „ \{0}

Из свойств коэффициента корреляции следует, что

^{С0Г (} « 1 ^ 1 ⁺ « 2 ^ 2 ⁺ ^ ^{+ а}Л „ , П ) =

= C ⁰ V ⁽ « ₁ ^ ₁ + « 2 ^ 2 ⁺ • • • ⁺ « „ £ „ , П )   =

D ^H D( «^ + « 2 ^ 2 ⁺ • ^{+ а}Л „ )

« 1^cov( ^ 1 , п ) ⁺ « 2^cov( ^ 2 , п ) ⁺ • ⁺ а „ cml а „ , п )

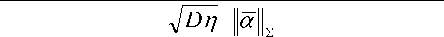
где ∑ – матрица ковариаций случайных величин ^1,^2,..., ^п,, относительно которой мы делаем предположение о строгой положительной определенности. Отметим, что это ограничение не нарушает общ- ности, так как вырожденность матрицы ∑ означает линейную зависимость индексов. В этом случае для построения универсального показателя мы можем использовать максимальный независимый набор индексов со строго положительной матрицей ковариаций.

Введя обозначение V = (cov(^ i ,n), cov(^ 2 ,n), ..., cov(^ n ,n)) , мы можем свести нашу задачу к нахождению максимума функции

/ „ ^{( а} ) =

« 1^V 1 ^{+ а} 2 ^V 2 ⁺ • ^{+ a} n^n

II ^ 1Z

( a , v )

II а _s ,

которая отличается от коэффициента корреляции постоянным множителем V Dп. Данная функция является однородной (степени 0), так как

I f „ ( O )H f „ (ка )| V 2 e R .

В силу неравенства Коши-Буняковского f„ (а) =

T α ⋅ v

α _Σ

a - s- ( s^-1 v )

α _Σ

^{( а} , S^{-1 v} ) ₂ α _Σ

^£1 =^ч v L =

= ( s ^{- 1} v ) T • S • S^-1 v = v ^T -S^-1 • v = || v| |_s - 1

функция f n имеет критические точки, коллинеарные вектору I ^-1 v , и в случае сона-правленности векторов сс и Z ^-1 v достигается наибольшее значение || v |_z -i .

Итак, мы показали, что поставленная задача имеет аналитическое решение. Однако найденные веса ос * = ! ^-1 v могут получиться отрицательными, что не соответствует понятию «взвешенной суммы». Для нахождения «классических» весов необходимо рассматривать задачу максимизации функции f n на множестве

M = | ( а 1 , - , а „ ): а . >  0 V i = 1, ^ , „ ; ]Г а , =1 1 , (1)

I i =1

которую мы сведем к рассмотренной выше задаче нахождения безусловного экстремума с помощью специального разбиения множества M.

Пусть δ ⊂ {1,2,...,n} – некоторый непустой набор индексов. Определим множество M δ с помощью следующего равенства:

M δ = M ∩{( α 1 , α 2 ,..., α n ) : α i > 0 ∀ i ∊ δ ; α i = 0 ∀ i ∉ δ }

Множества M δ₁ и M δ₂ , соответствующие разным наборам δ 1 и δ 2 , не пересекаются, при этом все множество M представляется в виде объединения ∪ M δ по всем непустым наборам δ ⊂ {1,2,...,n}. Следовательно, решение α⁻ ^*= a rgmaxf n | M , которое существует в силу компактности множества M, принадлежит одному из множеств M^* δ . Далее рассмотрим две возможности.

• 1.    Множество M^* δ соответствует набору δ , состоящему из единственного индекса k . В этом случае множество M^* δ содержит единственную точку, поэтому α⁻ ^* = (0,0,...,0,1,0,...,0) (в данном наборе единица располагается на k -ом месте).

• 2.    Множество M^* δ соответствует набору δ , мощности которого больше 1. В этом случае заметим, что

• f*(а)"; =тОг=f5,<а‘),

Σδ где ∑δ – минор матрицы ∑, соответствующий набору δ, а α⁻ δ, v⁻ δ – векторы размерности |δ|, составленные из компонент векторов α⁻ и ⁻v, образующих набор δ. Иными словами, ограничение функции fn на множестве M*δ является функцией такого же вида размерности |δ|. По доказанному выше, точка α*δ является критической для функции f|δ| и должна быть коллинеарна вектору ∑-δ1v⁻δ.

Таким образом, задача нахождения максимума функции f n | M может быть решена алгоритмически следующим образом. Пусть ∆ – множество непустых наборов δ ⊂ {1,2,...,n}, для которых все координаты вектора ∑ ^- _δ ¹ ⁻v _δ неотрицательны и хотя бы одна положительна, и

• 5 * =а rg max f ^(S ^^{1 г}₅ )

δ ∈ ∆

Тогда максимальное значение функции f n на множестве M равно f _{| δ |*} ( ∑ ^- _δ ¹ _* v⁻ _δ* ), а точка α⁻ ^* , в которой достигается максимум, получается из вектора ∑ ^- _δ ¹ _* ^⁻v _δ* добавлением n –| δ ^*| нулевых компонент.

Рассмотрим одно из возможных приложений построенного выше индекса – его использование как бенчмарка в соответствующей модели. Для иллюстрации мы выберем два инвестиционных фонда и построим для них последовательность θ n за период 2005 – 2007 гг. График и таблица скорости сходимости θ n для первого фонда уже рассматривались в предыдущем разделе, для второго – приведены далее ( рис. 6; табл. 12, 13 ; последнее значение на графике: θ = 0,1308).

При построении универсального индекса в данном случае весовые коэффициенты получаются равными α 1 = 0,2369, α 2 = 0,7631, а график последовательности θ n для этого индекса имеет следующий вид (рис. 7).

На этом графике последнее значение θ n равно 0,1129, что является своеобразным средним соответствующих величин инвестиционных фондов, участвующих в построении индекса.

Таблица 12. Динамика величины Δ в период 01.2005 – 06.2006

Квартал K	K 1	K 2	K 3	K 4	K 5	K 6
Длительность наблюдений (мес.)	3	6	9	12	15	18
Величина Δ	0,0718	0,1745	0,1839	0,2035	0,1467	0,0832

Таблица 13. Динамика величины Δ в период 07.2006 – 12.2007

Квартал K	K 7	K 8	K 9	K 10	K 11	K 12
Длительность наблюдений (мес.)	21	24	27	30	33	36
Величина Δ	0,0219	0,0211	0,0196	0,0269	0,0270	0,0087

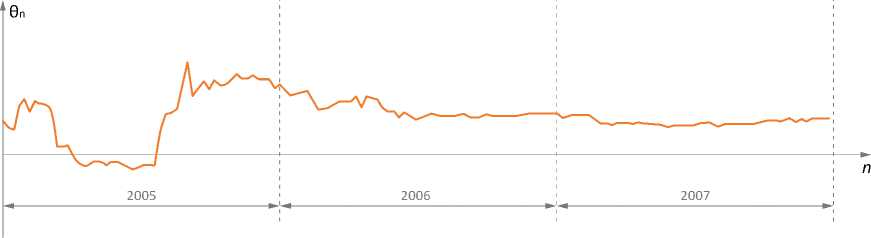
Рис. 6. Динамика оценки параметра для фонда 2 в период 2005 – 2007 гг.

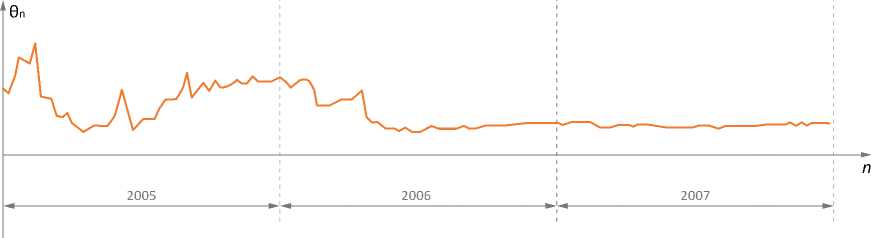
Рис. 7. Динамика оценки для универсального индекса в период 2005 – 2007 гг.