Об оценках погрешности кубатурных формул, точных для полиномов Хаара

Задача построения и исследования формул приближенного интегрирования, точных для некоторого заданного набора функций, ранее в основном решалась для интегралов, точных на алгебраических и тригонометрических многочленах. Квадратурные и куба-турные формулы, точные для системы функций Хаа-ра, можно найти в монографии И. М. Соболя [1], в которой точность формул приближенного интегрирования на конечных суммах Хаара использовалась при выводе оценок погрешности этих формул.

Описание всех минимальных весовых квадратурных формул, обладающих d -свойством Хаара, т. е. формул, точных на константах и функциях Хаара первых d групп, было проведено в [2].

В двумерном случае задача построения кубатур-ных формул, обладающих d -свойством Хаара, т. е. формул, точных для полиномов Хаара степеней, не превосходящих заданного числа d , решалась в [3-5], а исследование нормы функционала погрешности этих кубатурных формул на пространствах S p проводилось ^в [6].

Основные определения. В данной статье используется оригинальное определение функций x mj ( x ), введенное А. Хааром [7], отличное от определения этих функций в [1].

Двоичными промежутками imj назовем промежутки с концами в точках (j -1)/2m-, j/2m-1 (m = 1, 2, .., j = 1, 2, .., 2m-1). Если левый конец двоичного промежутка совпадает с 0, то будем считать этот промежуток замкнутым слева, если его правый конец совпадает с 1, то замкнутым справа. Остальные двоичные промежутки считаются открытыми. Левую и правую половины lm, j (без середины этого двоичного проме жутка) будем обозначать lm j и im j соответственно.

Система функций Хаара строится группами. Группа номер m содержит 2 ^{m -1} функций x m , j ( x ), где m = 1, 2, ., j = 1, 2, ., 2 ^{m -1} . Функции Хаара x m , j ( x ) определим следующим образом:

2(m 1)/2 при x e lm j, -2(m-1)/2 при x e im^., x j-) Ч

0 при x e[0,1]\ i j

0,5 [x m ,j( x - 0) + X „,/x + 0)], если x - внутренняя

точка разрыва,

-----                , m - 1      , m - 1                                                   m - 1

где l m , j = [( j - 1)/2   , j /2   ], m = 1,2, ..., j = 1,2, _ ,2 .

В систему функций Хаара включают также функцию x 0 0 ( x ) = 1, которая остается вне групп.

В двумерном случае полиномами Хаара степени d назовем линейные комбинации с вещественными коэффициентами мономов Хаара x m,. j,( x1) x m 2, j2( x 2), где m 1 + m2 = 0, 1, .,d;

[ 1, 2, ...,2 ^m n ^{- 1} , если m„ ^ 0, j n = i                          n

[0, если mn = 0, n = 1, 2, причем хотя бы один из коэффициентов при мономах Хаара степени d (m1 + m2 = d) отличен от нуля.

Будем рассматривать кубатурные формулы

1 1                               N

I [ f ] = JJ f ( x„x 2 ) dx dx 2 « Z C i f ( x *, x 2° ) = Q [ f ], (1) 0 0                                 i =1

где ( x ⁽ i ) , x 2 i ) ) e [0,1] ² - узлы формулы (1); C i - коэффициенты при ее узлах (вещественные числа), i = 1, 2, ., N , f ( x 1 , x 2 ) - функция, определенная и суммируемая на множестве [0,1] 2 .

Будем говорить, что формула (1) обладает d -свойством Хаара, или просто d -свойством, если она точна для любого полинома Хаара P ( x 1 , x ₂) степени, не превосходящей d , т. е. Q [ P ] = I [ P ].

Сформулируем определения классов функций двух переменных H _а( L 1 , L ₂, L 1, ₂) и S p ( A 1 , A ₂, A 1, ₂), приведенные в [1] для n -мерного случая.

Введем обозначения:

^A t 1 f ⁽ x L ^x 2 ) = ^{f ( x} 1 ⁺ t 1 , ^x 2 ) ^{- f (} x L ^x 2 ),

^A 1 ₂ ^{f ( x} 1 , x 2 ) = ^{f ( x} 1 , x 2 ⁺ t 2 ) ^{- f ( x} 1 , x 2 ^).

Пусть 0 < a < 1, L 1 , L ₂, L i, ₂ > 0. Тогда множество функций f ( x 1 , x ₂), определенных в единичном квадрате [0, 1] 2 и удовлетворяющих неравенствам

|A t i f ( x„ x 2 ) <  L i | t i |“, i = 1,2,

IAt1 A12 f (x1, x2)| < L1,2 It1 t2I для любых

(x1 + k11„ x2 + k212) e [0,1]2, ku k2 e {0,1}, называют классом Ha(L 1, L2, L 1,2), а константы L 1, L2, L1,2 - определяющими постоянными этого класса.

В [1] показано, что множество функций f (x 1, x2), принадлежащих всем классам Ha(L 1, L2, L 1,2) (со всеми возможными L 1, L2, L 1,2, значение a фиксировано), является линейным пространством, на котором норма вводится по формуле

I H _a = max {^ ^А 1 ' ^{f (} x l , x 2 ) I t ll ^а ,

^Sup| ^А 1 2 ^{f (} x i , ^x 2 ’| t 2I ^а , ^SUP| ^А t 1 ^А 1 2 ^{f (} x l , ^x 2 ’ t l ¹ 2| ^а } ,

8 N [ f ] = I [ f ] - Q[ f ] =

11                    N

= J J ^{f ( x} 1 , ^x 2 ) dx l ^dx 2 ^- X ^Ci^{f (} x l i ’ , x 2 i ’ ’.

0 0                                 i =1

В [6] были введены величины

где точные верхние границы берутся по всем

( x 1 + к₁1 1 ,x ₂ + к ₂ 1 ₂ ) е [0, l] ² , к₁,к ₂ е { 0,1 } .

Введенное линейное нормированное пространство обозначается H _а. При этом все функции f ( x 1 , x ₂), отличающиеся постоянными слагаемыми, считаются за одну функцию.

Множество функций f ( x 1 , x ₂), определенных в единичном квадрате [0, l] 2 и представленных в виде ряда Фурье-Хаара

x q ( m, ) = 2   m- ^-"-^-2

X

и  2 ml ^{- 1}

^{f (} x l , ^x 2 ’ = c 0 ⁺ X X ^',0 X m l , j l ⁽ x l ’ ⁺ m l =' j l ='

и 2 ^m 2 ^{- 1}

+ X X c0^2 Xm2,j2(x2) + m2 =' j2 ='

и „ 2 m l ^{- 1} 2 m 2 ^{- 1}

+ X X X X j ’ X m l , j l ( x l ) X m 2 , j ( x 2 ) m l =1 m 2 =1 j l =1 j 2 =1

удовлетворяющими условиям и             Г2 ml-1, pl 'p

A™0f) =X 2O'-11" X j p   S Al, ml =            L ji ='           _

и

A P "- f ) = X 2 ⁽ * ^{1 -W 2}

m 2 =1

2 m 2 - 1           1 ¹ P

X c0,mHp S A j2 =1             _

A П f ) =

= X X 2 ( m i -l’^+O m 2 -1)^ m i =1 m 2 =1

2 mi - 1 2 m 2 - 1

X X cmVm2'lp j1 =' j 2 ='

V p

’

где p > 1, A _V, A ₂, A _V , ₂ - вещественные константы, определяется как класс S_p ( A _V, A ₂, A _V , ₂). В [1] доказано, что множество функций f ( x _V, x 2 ), принадлежащих всем классам S_p ( A _V, A ₂, A _V , ₂) (со всеми возможными A _V, A ₂, A _V , ₂, значение 1 <  p < да фиксировано), является линейным пространством, на котором норма вводится по формуле

||f || S_p = A «( f ) + A^ ( f ) + A j²’ ( f ). (4)

Данное линейное нормированное пространство обозначается S_p . При этом все функции f ( x _V, x ₂), отличающиеся постоянными слагаемыми, считаются за одну функцию.

Оценки нормы функционала погрешности ку-батурных формул на пространствах H _а. Обозначим через 8 N [ / ] функционал погрешности кубатурной формулы (1):

2 mn ^{- 1}

X jn =1

N

X C i X . . j ( x ni ’ ) i =1

n = 1, 2,

X q ^1,2)( m _V , m ₂ ) = 2 ^{- (} m i ^{- 1)}/^{2 - 0 m} 2 ^{- 1)/2}

2 m i - 1 2 m 2 - 1

N

q ₁ ^V q

q ₁ ^V q

X X X C i X m _V, j_V ⁽x l i ^{) )} X m ₂, j ₂ ⁽ x 2 i ’ ’

-/ 1 =' ^j 2 ='

i =1

,

где m 1 , m 2 = 1, 2, ..., q > 1, а также доказаны неравенства, справедливые для кубатурных формул (l), обладающих d -свойством:

X q ^,'²'0 m i , m 2 ) s 2^{1, р} (2 d )"^{, P} , X qn ’ ( m n ) = ( 2 d ) ^- '^{, P} , n = 1,2,

и

1 8 _N [ f ]| S X 2 ⁽ m i ^{- 1}’C ^{+ 0 m} 2 ^{- 1}’C m ' + m 2 =2

x X ( q  m m l , m 2 ) + X 2 ⁰ " ’^-1,,2

m ' =1

+ X ₂( m 2 -1)/2 m 2 =1

2 m i - 1 2 m 2 - 1

x x c mj ’I ^p j l = 1 j 2 = 1

2 m i ^- '

x c m :,0| ^p

2 m 2-i x c0jm;|p j 2 =1

-1V p

X

- V p

X™ ( m l )

_- ^V p

X ' q ^2,0 m Л    (8)

В [1] доказаны утверждения, которые в двумерном случае принимают следующий вид.

Лемма 1. Для коэффициентов Фурье-Хаара суммируемой функции f ( x 1 , x 2 ) класса H _а( L 1 , L ₂, L _V , ₂) имеют место следующие неравенства:

L⁽ j l , ^j 2 )1 <  ^^{- 0 m} 1 ^{+ m} 2 )^{( a +} V²) ^{- 1} T

I c m ' , m ₂ I ^{S 2}                        L 1,2 ,

J c ⁽ j i ’ J <  2 - ^m i (^a +V^{2) -} V² L ' | c ^{( j} 2 ’ J <  2 - ^m 2 ^(a+11^2)-11² l 2

Лемма 2. Если a p > 1, то

H a ( L ' , L 2 , L ,,2 ) c S p ( A ' , A 2 , A ',2 ),

где

A = 0,5 L /(2 ^a - 2 ^{V p} ), i = 1, 2;

A ',2 = 0,5 L ',2/ (2 “ - 2 ^Vp ).

Лемма 3. Для функции f ( x 1 , x ₂) класса H _a( L _V, L 2 , L i, ₂) норма

II ^f ll _{H a} ^S max { L i , ^L 2 , L 1,2 } .

Если для f ( x _V, x 2 ) выбрать наименьшие возможные определяющие постоянные L _V, L ₂, L ₁₂, то

II Ah _a = ^max { L i , ^L 2 , L i,2 } .

Имеет место следующая лемма.

Лемма 4. Для любого натурального d и любого -1 <  t < 1 справедливо следующее равенство:

5 ( к - 1) t ^k = dt ^{d + 1} (1 - t ) ^{- 1} + t d ^{+ 2} (1 - t ) ^{- 2} .     (10)

к = d +1

Лемма доказывается с помощью почленного интегрирования ряда ю

5 ( к - 1) t ^{k - 2} .

к = d +1

Теорема 1. Если функция f ( x 1 , x ₂) е H _а, то для нормы функционала погрешности кубатурной формулы (1), обладающей d -свойством, имеет место следующая оценка:

||б _N\\H * <  2 ^{- а d - 2} ( d (2 ^а - 1) ^{- 1} + (2 ^{а + 2} - 3)(2 ^а - 1) ^{- 2} ) . (11)

Так как в последней сумме каждому значению m 1 + m ₂ = к соответствует ( к - 1)-е слагаемое, то в силу равенства (10) имеем

A p *-²⁾( f ) <  ' ^p L 1,2 5 ( к - 1)2

к >  d

= d X 2 ^{- d (a - 1 p ) - 1 -} V ^p ( 2 ^{a + 1}

+ 2 - d (^{a -} V p ) ( 2 ^{a + 1}

- ^{к (a -} V p ) =

2 ^{1 p + 1} )

2V p+1)

-2

-1

+

L 1,2 .

Применяя (7), (13), (14), из (8) с учетом (12) получим

I б N [ f ]| <  2 ^{- а d - 1} { ( L + L ₂ ) ( 2 ^а - 2 ^{1 p} ) ^{- 1} +

+ 0,5 L 1, ₂

Тогда

d ( 2 ^а - 2 ^{1 p} ) ^{- 1} + 2 ^{1 p} ( 2 ^a -

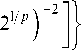
Д о к а з а т е л ь с т в о. Пусть p > 1/а, а L 1 , L ₂, L 1,2 - определяющие постоянные одного из классов H _а( L 1 , L ₂, L 1, ₂), содержащих функцию fx 1 , x ₂). Тогда в соответствии с леммой 2

|б n [ f ]| <  2 ^{- а d - 1} { ( L 1 + L 2 ) ( 2 ^а - 1 ) ^{- 1} +

+0,5 L1^ Гd (2а - 1)-1+(2a-1)-21,

^{f (} x 1 , x 2 ) ^е S p ⁽ A 1 , A 2 , A 12 ),

где

4 = 0,5 L /(2 ^a - 2 ¹ p ), i = 1, 2;

A 1,2 = 0,5 Д,2/ (2 ^а - 2 ¹ p ).

поскольку выражение в левой части (16) может быть представлено в виде

inf { p > 1 а ^

2 -а d -1

(L1 + L2 )(2а -

2^ p )-1 +

Введем следующие обозначения:

A ™( f ) = 5 2(' ^{- 1v2}

A ™( f ) = 5 2 < m 2^-№ m 2 >  d

^ m1 1

5 jp

Л=1

2 ^m 2 ^{- 1}

5 ■0^J m 21 ^p j 2 =1

A O’²^ f ) = 5 2⁽ m "W m 2-1)/2 m 1 + m 2 >  d

В силу (9)

A⁽ n ) ( f ) <  5 2 ^{( m} n " ^1)/2 m_n >  d

2 m - 1 2 m 2 - 1

5 5 k m 1 , m ^{2 ,}| ^p

2mn-1 (2-mn (a+V2)-V2 l )P

= 2 ^{- d (a - v p} ) L_n ( 2 ^{a + 1} - 2^{V p + 1} ) 1 , n = 1, 2.

"11 P

л 1 P

.

Применим первое из неравенств (9) к выражению A П f ):

X

A°’2)( f) <   5   2(m -1)/2+(m2 "1)/2 > m1+ m 2 > d

2 ^m 1 ^{- 1} _X 2 ^m 2 ^{- 1} _X ( 2 ^{- ( m} 1 ^{+ m} 2 ^{)(а + 12) - 1} l ₁₂ ) p

-11 p

= 2 ^{- 2 - 2}'' P L 1₂ 5    2 -( ^m 1 ⁺ m ^2)(а-^ p )

m 1 + m 2 >  d

+ 0,5 L_x 2 ^ d ( 2 ^а - 2 ^{1 p} ) ^{- 1} + 2 ^{1 p} ( 2 ^а - 2^{V p} ) -2 ^ .

Выберем в качестве L 1 , L ₂, L 1, ₂ наименьшие возможные определяющие постоянные для f ( x 1 , x ₂). В соответствии с леммой 3 из неравенства (16) получим:

I б N [ f ]| <  2 - ^а d ^{- 1} ] 2 ( 2^а - 1 ) - ¹ + 0,5 Г d ( 2^а - 1 ) - ¹ + ( 2^а - 1 ) - ² 111 f_{H а} .

Отсюда следует неравенство (11). Теорема доказана.

Рассмотрим теперь кубатурные формулы (1), обладающие d -свойством, число узлов которых N ~ 2 d при d ^ ». Указанному условию удовлетворяют минимальные кубатурные формулы, т. е. формулы с наименьшим возможным числом узлов, обладающие d -свойством, которые были построены в [3] для значений d > 5 (число узлов каждой такой формулы N = 2 ^d - Х( d), где

| 2 ^{d 2 + 1} - 2      при d = 2 1 ,

л( d ) = <

[ 3 x 2 ^{( d - 1)/2} - 2 при d = 2 1 - 1, l = 3,4,....

Тогда в силу (11) имеет место следующая теорема.

Теорема 2. Если кубатурная формула (1), число узлов которой N ~ 2 ^d при d ^ », обладает d -свойством, то норма ее функционала погрешности удовлетворяет неравенству

II ^б n L _: <® ( N ),

где 0 ( N ) ~ 0,25 N ^{- а} log₂ N ( 2 ^а - 1 ) -1 при N ^ « .

В [1] рассмотрены кубатурные формулы

11 1

JJ - J f ( x i , x 2 , 00 0

N

-     Z f ( x ^, x 2°, . , хП?)

N = 1

с 2 d узлами ( x ^{( , )} , x 2 i\ . , x ^ ) ) e [0,1] n , образующими Π_τ-сетки (0 ≤ τ <  d ), и доказано, что они точны на полиномах Хаара степеней s ≤ d – τ. В данной статье доказано асимптотическое равенство [1] для нормы функционала погрешности таких формул на пространствах H α

δ N _H * = O ( N ^{- α} ln ^{n - 1} N ), N → ∞ .

Очевидно, что норма функционала погрешности δ N H * формул, изученных автором данной статьи, при N ~ 2 d , d → ∞ тоже ограничена по сравнению с N -^α ln N , N → ∞.

В частности, условию N ~ 2 d , d → ∞ удовлетворяют кубатурные формулы, построенные в [3]. Данные формулы являются в некотором смысле обобщением формул, исследованных в [1] для случая n = 2. В то же время они, будучи минимальными формулами приближенного интегрирования, обеспечивают наилучшую поточечную сходимость δ N [ f ] к нулю при N → ∞.

• 1.    Соболь И. М. Многомерные квадратурные формулы и функции Хаара : монография. М. : Наука, 1969.

• 2.    Кириллов К. А., Носков М. В. Минимальные квадратурные формулы, точные для полиномов Хаара // Журн. вычисл. математики и мат. физики. Т. 42. № 6. С. 791–799.

• 3.    Кириллов К. А. Построение минимальных куба-турных формул, точных для полиномов Хаара высших степеней в двумерном случае // Вычисл. технологии : спец. выпуск, посвящ. 50-летию Краснояр. гос. техн. ун-та. Т. 10. Красноярск, 2005. С. 29–47.

• 4.    Noskov M. V., Kirillov K. A. Minimal Cubature Formulas Exact for Haar Polynomials // J. of Approximation Theory. 2010. Vol. 162, Iss. 3. P. 615–627.

• 5.    Кириллов К. А. Алгоритм построения минимальных кубатурных формул, обладающих d -свойством Хаара в двумерном случае // Журн. Сиб. федер. ун-та. Серия «Математика и физика». 2010. Т. 3. № 2. С. 205–215.

• 6.    Кириллов К. А., Носков М. В. Оценки погрешности на пространствах S p кубатурных формул, точных для полиномов Хаара в двумерном случае // Журн. вычисл. математики и мат. физики. 2009. Т. 49. № 1. С. 3–13.

• 7.    Haar A. Zur Theorie der orthogonalen Funktionen-systeme // Math. Annalen. 1910. Vol. 69. S. 331–371.

On the spaces H α the estimates are found for the norm of the error functional δ N [ f ] of cubature formulas possessing the Haar d-property in the two-dimensional case.