Об оценке достоверности информации, преобразованной нелинейным методом

В работе решается задача преобразования информации. При этом известной является информация о распределении температуры в момент времени T >  0, а требуется определить распределение температуры в начальный момент времени и оценить погрешность этого распределения. Для решения этой задачи использован нелинейный метод проекционной регуляризации, приведенный в [1], и показано, что при решении этим методом оценка погрешности получается гораздо лучше, чем при решении аналогичной задачи оптимальным линейным методом, приведенным в [2].

Постановка задачи

Пусть H – гильбертово пространство, A – инъективный линейный ограниченный оператор, отображающий H в H и множество значений R ( A ) оператора A всюду плотно в H .

Рассмотрим операторное уравнение

Au = f ; u е H , f e H .                    (1)

Предположим, что при f = f ₀ существует решение u 0 e H уравнения (1), но точное значение правой части из-за ошибки измерения обычно не известно, а вместо него даны f _s е H и 3 >  0 такие, что

II fs - f0I < 3.

Требуется, зная f _s и 3 , определить приближенное решение u s уравнения (1) и в предположении, что u 0 принадлежит классу корректности M_r = BS r , найти уклонение приближенного решения от точного || u s - u о|| , где B - линейный ограниченный оператор, отображающий H в H , удовлетворяет тем же условиям, что и A , S r = { v ; v ^е H ,|| v || <  r } .

Определение 1. Множество M_r будем называть классом корректности для уравнения (1), если — 1

сужение A_Nr оператора A на множество N_r = AM_r равномерно непрерывно.

Лемма 1. Для того, чтобы M_r было классом корректности для уравнения (1) необходимо и достаточно, чтобы сужение A N -¹ оператора A ¹ было непрерывно в нуле [2].2

Определение 2 . Семейство операторов { T s : 0 <  3 <  S o } будем называть методом приближенного решения уравнения (1) на множестве M_r , если для любого 3е ( 0, 3 ₀ ] оператор T _s непрерывно отображает H в H и T _s f _s ^ u ₀ равномерно на множестве M_r при S ^ 0 и ||fs - Au 0|| <  S .

Из условий, наложенных на операторы A и B на основании леммы, доказанной в [3], имеют место полярные разложения этих операторов A = QA и B = BP , где Q и P - унитарные операторы, A = V A * A , B = V BB * . Кроме того, предположим, что спектр Sp ( A ) оператора A совпадает с отрезком [ 0, 11 A ||] , а

B = G ( A ) ,                                  (2)

где G ( A ) строго возрастает и является непрерывной на отрезке [ 0, 11 A ||] функцией такой, что G ( 0 ) = 0.

Из полярного представления оператора A следует, что уравнение (1) можно заменить эквивалентным:

Au = g ,                                 (3)

где g = Q * f , а Q * - оператор, сопряженный Q .

Лемма 2. Пусть M r = BS r , а B = V BB* [2], тогда

M r = BS r .

Как указывалось выше, при g ₀ = Q * f ₀ существует точное решение u 0 уравнения (3), но точное значение g ₀ нам не известно, а дано g ₃ и 3 такие, что

II g 3 ^- g 0I |< 3 .

Требуется по g ₃ и 3 определить и ₃ и оценить I U 3 - и 01| при условии, что U ₀ £ M_r .

Для решения данной задачи применяется нелинейный метод проекционной регуляризации, подробно описанный в следующем пункте, который позволяет при условии, что и 0 £ M_r получить оценку

||и3 -и0I|5 7rG|a(3)|, где a(3) - значение параметра регуляризации, выбранное из уравнения raG (a) = 3.

Методика решения задачи

В методе проекционной регуляризации [1] используется регуляризующее семейство операторов { P _a :0 <  a < || A ||} , определяемых формулой

A ₁

P a g = I СТ dE ^ g , ^{а £}(°’1 A l О,           (4)

a где {Eg :0 < ст < ||A|} - спектральное разложение единицы E , порожденное оператором A .

Приближенное решение уравнения (3) определим формулой u з = Pag3.

Для выбора параметра регуляризации a по исходным данным (g3, 3) в формуле (5) исполь- зуем уравнение

II A^{ua -} g 3 || =^{16 3 2}.

Лемма 3. Если ||gs|| > 43 ,то существует зна чение a = a(gs, 3), удовлетворяющее уравнению

(6) [2].

В дальнейшем приближенное решение определим формулой

= / P a ( g 3 , 3 ) g 3 при IMl >  ^{4 3} , 0,       при | Ы <  ^{4 3} -

Из (4), (6) и (7) следует, что для любого значения g ₃ £ H приближенное решение u ₃ уравнения (3) определено однозначно.

Лемма 4. Оператор Т ₃ , определяемый формулой (7), непрерывен на пространстве H [2].

Обозначим через a(3) значение параметра регуляризации, выбранное из уравнения raG (a) = 3.                              (8)

Лемма 5. Пусть оператор P _a , определен формулой (4), тогда [1, с. 42]

P a l= a

Лемма 6. Если || g _s || > 4 3 и a ( g ₃ , 3 ) определено (6), то для любого a >  0 из того, что

II AP a g 3 - g 3 || <  43                            (9)

следует [2]

II P ll -| P a ( g 3 , 3 )||.

Лемма 7. Пусть и 0 £ M_r , || g ₃ 1| >  4 3 , тогда для значений < a ( g _s , 3^х ) и a ( 3 ) выполняются следующие соотношения [2]

II a^u 3 ^{( 3 ) -} g 3 || <  ^{3 3 ,} «( g s ^{, 3} ) ^ ^a ( ³ ) и

I ^P & ( g 3 , 3 ) ^g 3 ^{- P} & ( g 3 , 3 ) ^g 0I I <  ^rG [ ^{a ( 3 )} ] .

Следуя [5], определим функции to 1 ( т , r ) и ю ( т , r ) :

& 1 ( т , r ) = sup {|| u 1 - и ₂|| : и 1 , и ₂ £ M_r ,|| Au j - Au ₂|| <  т },

® ( т , r ) = sup {|| u ||: и £ M_r ,|| Au || <  т } , т , r >  0, (10) которые связаны друг с другом формулой [1]

ю 1 ( т , r ) = ® ( т ,2 r ) .

Пусть ст _т - решение уравнения rG ( ст ) ст = т .

Лемма 8. Если выполнены все условия на операторы A и B , сформулированные выше, а т <  r ||AB |I, то справедлива формула [2].

№ ( т , r ) <  rG ( ст ( т ) ) .

Теорема 1. Пусть u0 е Mr, ||g|| > 43, u3 определен формулой (7), и C(3) - формулой (8), тогда справедлива оценка

|| ^u3 ^{- u} oil < ^{7 rG с} ( ³ )| .

Доказательство .       Из равенства

О' ( gs , 3 )      П                  1

u _o ³   = P & ( _{g 3} , 3 g о и формулы (4) получаем

u ^{( g 3 , 3 )} = У - dE . g о -                (11)

^с ( g3 ³ ) ^

Обозначим через Н ₃ подпространство, определяемое формулой

Н ₃ = ( E - E-, Дн . ³ \         « ⁽ g s ^{, d )} /

Тогда из равенства и о = Bv» следует и“'g33 U Bvз,                             (12)

где v ₃ - метрическая проекция элемента v ₀ на подпространство Н ₃ .

Из (4), (7), леммы 6 и (11) получаем

I A.^{3 )} - Au , | |² =

A

= f d ( ^E a ⁽ g 3 ^- g 0 ), g 8 ^- g 0 ) <              ⁽¹³⁾

a (g g , 3 )

<| ^g 3 ^- g 0Ц² <  ³ 2 , а из равенства Au ₃ - g ₃ = 43 и соотношения (13)

следует

I Au(g3,3)- g3|| < 53, а значит

I Au'(g3,3)- Au 0||< 63.

Так как из (12) следует, что и ^ ^{( g 3 , 3 )} = Bv ₃ , где ||v ₃11 <  r , то из (15) следует

JuC(g3,3)-и0||< №1(63,r).

Из леммы 8 , соотношения (16) и того, что № ( 6 3 , r ) = ю ( 6 3 ,2 r ) следует

I u(g3,3)- u 0I < 6 rG [a(3)].

Так как из леммы 7 а ( g ₈ , 3 ) > С ( 3 ) , то

—--Г <— .

« ( g 3 , 3 ) с ( 3 )

а значит

I u ^{( g 3} , ^{3 3}

3 с ( 3 ) .

Из (8) и (19) следует

I ^u “ ^{( g 3 , 3 ) - u} ₃ || <  rG [ а ( 3 ) ] .

Из (17) и (20) следует утверждение теоремы.

Результаты

Покажем нахождение оценки погрешности нелинейного метода проекционной регуляризации на примере решения обратной задачи Коши для уравнения теплопроводности. Для этого рассмотрим уравнение теплопроводности дu (x, t) д2 u (x, t)

-------- =--------- ■    - co < V < co д t          дx2    ’                  ,          (21)

t e( 0, T], T > 1, где u (x, t) е C{(-”, ^)x [0, T]} A C2,1 {(-”,M) x (0, T]} для любого tG(0,T],

^u ( ^x , t ) , ^u x ( ^x , t ) , ^u xx ( ^x , t )^e L 2 ( ^^; - ~ ) A L 1 ( -^; . ~ ) и существует функция ^ ( x ) е L 1 ( -^ , ^ ) такая, что для любого t G ( 0, T ]

I ^{u ( x} , t )|+ ^{д u} д x’^{1 )} <  z ^{( x )} ,

- ^ <  x < ^ .

Пусть дано распределение температуры f ( ^x )^G L 2 ( ^^; - ~ ) ^A L 1 ( -^ , ^ ) в момент времени T >  0

u ( x , T ) = f ( x ) ; -^< x <^ ,            (23)

а начальное распределение u ₀ ( x )

u ( x ,0 ) = u 0 ( x )                                (24)

требуется определить.

Предположим, что при f ( x ) = f ^ ( x ) существует u 0 ( x ) такое, что производная u 0 ( x ) является четной, кусочно-непрерывной функцией и u ₀( x ), u 0 ( x ) g L 2 ( -^ , ^ ) A L 1 ( -^ , ^ ) , а также решение задачи (21), (23) при нем удовлетворяет условию u ( x , T ) = f J ( x ) , но точное значение f 0 ( x ) нам не известно, а вместо него даны некоторые приближения f ₈ ( x ) е L 1 ( -^ , ^ ) A L 2 ( -^ , ^ ) и 3 >  0 такие, что

||^f3 ( ^x )^{- f} ) ( ^x )|| _L 2 <  ³ .                       (25)

Требуется, используя исходные данные ( f _s , 3 ) задачи (21), (22), (24), определить приближенное решение u ₅ ( x ) е L 2 ( -^ , ^ ) и оценить величину || u 3 ( x ) - u ₀ ( x )||

Для решения задачи (21), (22), (24) используем преобразование Фурье F , тогда получим

u ; ( X ,t ) = - X² u ( X ,t ) ; X e ( -w , w ) , t e ( 0, T ] (26)

й ( X ,T ) = f ( X ) ; X e ( -w , w ) ,             (27)

где u ( X , t ) = F [ u ( x , t ) ] , a f ( x ) = F [ f ( x ) ] .

Решая задачу (26), (27), сведем ее к операторному уравнению

a >  0 такого, что для любого достаточно малого числа e >  0 :

w

-w L

13 ( 1 - e )

I ui 0 ( X )|² d X <  a ,

AU ( X ) = e ^{- X2}TU ( X ) = f ( X ) ; U ( X ) , f ( X ) e L 2 ( -w , w ) .

Из условий четности и кусочной непрерывно сти производной u0' (x) следует, что u 0'( x )= L Ii( x ) + ^( x),               (29)

i = 1

а из (25) и теоремы Планшереля [7, с. 411], что

I АЙ 0 ( X ) - f 3 ( X )|| < 3 ,                       (36)

где ^u 0^{( X )} = ^{F [ u} 0 ( ^x ) ] , ^{а f} 3 ( ^X ) = ^{F [ f} 3 ( ^x ) ] .

Применяя к решению задачи (28) метод проекционной регуляризации [1], введем регуляризующее семейство операторов | P_a : a >  0 } , определяемых формулой

^P a ^f ( X ) ='

e ^{X T}f ( X ) ; X <  a 0; X >  ^a .

где для любого i e 1, n существуют числа a i * 0 и

Таким образом, приближенное решение d g ( X ) в уравнении (28) определим формулой

x i > 0 такие, что

u a ( X ) = P a f 3 ( X ) ,

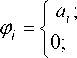
^{- x} i <  ^x <  x i , x < - x i , x >  x i

а

а

^ ( x ) e W 22 ( ^* , ^{w, )} .

Таким образом, из (30) следует

для выбора параметра регуляризации

a ( f _s , 3 ) в формуле (37) используем уравне-

ние

I Au i ^a _s ( X ) - f _s ( X )| L 2 2 = 16 3 ² .

I i ( ^X ) = ■

² a i

E

sin x_tX X

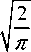
- w <  X <  0,0 <  X < w ,

X = 0,

Из (37) и (38) определим приближенное решение uig (X) уравнения (28) формулой ug (X) = uga(g3,3)(X).

Из теоремы 1 и формул (35)–(38) следует оценка

где

i (X ) = F [tp^x ) ] .

Лемма 9. Пусть | ( x ) e L 1 ( -w , w ) П L ₂ ( -w , w ) и    | ( X ) = F [ g ( x ) ] , тогда из того, что

||ui3 ( ^X ) - zⁱ 0 ( ^X )|| < 7 ^G [ a ( ³ ) ] ,

| ( x ) e W ₂ ^p ( -w , w ) , p e ( 0, w ) следует

в которой функция G _e ( ст ) , следуя (35) и (28), определяется параметрически:

w

II I x )l Wp_? = J 1 + X ^{2 p}| I ( X )| ² d X <-. .

-w

Доказательство приведено в [8, с. 212].

Из (32) следует, что для любого достаточно малого числа e >  0

<

-λ²T a = e

X e ( -w , w )

а a ( 3 ) - уравнением

—( 1 - e )                           ----

| ( x ) e W ₂²      ( -w , w ) ,        i e 1, n .      (33)

a = 3.

Значит для любого i e 1, n существует c i такая, что w                            2

J [ 1 ₊ X ^{1 - e} ] | i i ( X )| ² d X <  4 e ₊ c .        (34)

-w

Из условий, которым удовлетворяет функция u 0 ( x ), будет следовать существование числа

Так как оценка (39) выполняется при любом

^{e e} ( 0,2 ,

то выберем значение e ( 3 ) , минимизи-

рующее эту оценку. Ввиду непрерывности функ-

ции 7

по e на полуотрезке [ 0, 2

и стремление ее к бесконечности при г ^ 0, сле дует существование г (5) е [ 0, 2

такого, что

7J тз гУ^'"^)'

= min 7, / —G ( « ( 5 , г )).

е е( 0,1] N г г V ”

Тогда из (39)-(42) для U5 (2) будет справед- лива оценка

II «8 (2)~ u0 2   7 ^GE (») - 'г (5 ))]■ (43)

Применяя к U ₅ ( 2 ) обратное преобразование Фурье F ¹ и беря действительную часть, получим приближенное решение u ₅ ( x ) = Re ^ F ^-1 ( U ₅ ( 2 ) ) ] обратной задачи (21), (23), (25). Для этого решения по теореме Планшереля ([7, c. 411] будет справедлива оценка (43).

Упрощая оценку (43), получаем

3 a 3 I Г" 3 / _ х

||-5 ( x ) “ - о ( x )|| ^ 7 4 2 e ² T ⁴^lnln 3 In ⁴ f 3 1 .