Об оценке эффективности силовой работы некоторых типовых элементов тонкостенных конструкций

Тонкостенные пространственные конструкции, состоящие из участков пластинок и оболочек, подкреплённых стержнями (пояса, стойки, стрингеры и т.п.), широко распространены в силовых конструкциях летательных аппаратов. Масса конструкции самолёта столь сильно влияет на его эффективность, что её определение и постоянное уточнение в ходе проектирования представляет собой одну из главных и наиболее трудных задач в общей проблеме весового проектирования самолётов [1, 2]. Принимая в качестве обобщённой рабочей модели силовой конструкции её представление как устройства для передачи сил, в статье рассмотрены некоторые типовые проектные задачи с целью отыскания и обоснования рациональных решений при выборе способов передачи сил – элементов силовой схемы конструкции. Для оценки эффективности вариантов решений по критерию минимума массы конструкции используются специальные показатели – «силовой фактор» и «коэффициент силового фактора» [2]. Общие принципы такого подхода к оптимизации и оценке весовой эффективности силовых конструкций известны уже несколько десятилетий [3, 4]. Известны также примеры его удачного применения для решения сложных проектно – конструкторских задач [5]. В работе [6] показаны примеры использования этого подхода на ранних стадиях проектирования летательных аппаратов с нетрадиционными схемами и компоновками. Вместе с тем, широкое использование названных показателей в проектной практике сдерживается недостаточной изученностью их свойств, а также результативности их применения для решения конкретных задач. Козлов Дмитрий Михайлович, кандидат технических наук, доцент, профессор кафедры конструкции и проектирования летательных аппаратов.

Силовой фактор G представляет собой интегральную количественную характеристику силовой работы конструкции, отражающую величину и протяженность действия внутренних усилий в ней. Для отдельного стержня длиной l , испытывающего растяжение или сжатие от действия приложенной к его концам силы Р , внутреннее усилие N по модулю равно внешней силе Р . Тогда силовой фактор стержня

G =I N I l .                  (1)

Для фермы из n стержней, в каждом из которых действует внутреннее усилие с модулем I N_i I, где i – номер стержня, значение силового фактора G вычисляют по соотношению

G = ∑ _{i = 1} N i l i ; ( i=1, 2,…, n ),      (2)

где l_i – длина стержня с номером i .

В общем случае для произвольной конструкции

G = σ экв dV ,             (3)

V где σэкв – напряжение одноосного напряженного состояния, эквивалентное по удельной потенциальной энергии действительному напряженному состоянию конструкции в объеме dV или подсчитанное согласно принятой теории прочности;

• V – объем материала в конструкции.

Силовой фактор имеет ряд свойств, которые позволяют использовать его в качестве критерия эффективности силовой работы конструкции и выбора лучшего варианта силовой схемы [4]. Здесь отметим только два из них.

• 1)    Величина G определяется силовой схемой конструкции, т.е. типом элементов, их количеством, способами соединения между собой и расположением в пространстве. Для статически определимых конструкций величина G не зависит

от соотношений жесткостей силовых элементов, а для статически неопределимых, как показывают вычислительные эксперименты, зависит слабо.

• 2)    Теоретически необходимый объем материала полнонапряженной конструкции с некоторой силовой схемой V_T может быть приближенно оценен через G и величину допускаемого (разрушающего) напряжения [ ст ] с использованием однократного расчета внутренних усилий для некоторого рационального начального распределения жесткостей элементов по простейшему соотношению

G

V      [ст].                        (4)

Действительно, для полнонапряженной фермы имеем

V = х i : : [ СТ ]। nv, = х i :^, (5) где F_i – площадь поперечного сечения стержня.

Аналогичный результат получается для конструкций из мембранных (тонкостенных) элементов, если использовать в качестве меры внутренних усилий эквивалентные потоки усилий – произведения эквивалентных напряжений в элементах и толщин элементов

G : V i:" R S :V^" СТ „ AS, , (6) =1 i=i экв.i i i , где Ri,, δi , Si – соответственно эквивалентный поток усилий в элементе с номером i, толщина и площадь этого элемента.

Для полнонапряженной конструкции с эквивалентными напряжениями, равными [ ст ] очевидно

Vt =СТ : X" [СТ] RS: X “AS,. (7)

Из определения силового фактора, а также из выражений (4) – (7) со всей ясностью следует: конструкцией минимальной массы может быть такая (конструкция), в которой внешние нагрузки передаются наименьшими внутренними усилиями и по наиболее коротким путям, обеспечивая по возможности меньшее значение силового фактора. Для выбора лучшего варианта силовой схемы конструкции достаточно для каждого варианта произвести расчет внутренних усилий и вычисление значений силового фактора практически для любого разумного распределения жесткостей элементов силовой схемы. Это большое достоинство физической величины «силовой фактор». Ее некоторым недостатком является то, что G – величина размерная. Этот недостаток снимается путём перехода к безразмерной характеристике эффективности силовой работы конструкции – коэффициенту силового фактора C_к

[2]. Его значение получают как отношение значения силового фактора G к произведению некоторой характерной для данной конструкции внешней силы Р и характерного её линейного размера l , отражающего направление и путь передачи характерной силы

C = G

k Pl .

Физический смысл коэффициента силового фактора можно представить как величину силового фактора, соответствующего передаче конструкцией характерной единичной силы на единичное же характерное расстояние. Коэффициент силового фактора удобно использовать для сравнения эффективности силовой работы конструкций, имеющих одинаковое или близкое назначение и отличающихся либо величиной действующей нагрузки, либо размерами, либо обеими характеристиками одновременно. Отдельный интерес представляют значения коэффициента силового фактора и их соотношения для разнообразных конструкций, в том числе типовых (элементарных). Этот интерес объясняется следующим.

Любую силовую конструкцию можно рассматривать как устройство для передачи сил. Передачу внешней силы (сосредоточенной или распределённой – не имеет значения) в произвольном направлении можно представить как совокупный результат передачи её по направлению действия силы и перпендикулярно к этому направлению с одновременным уравновешиванием возникающих при переносе силы изгибающих или (и) крутящих моментов. Естественно предположить, что различные способы передачи (уравновешивания) этих силовых факторов, отличающиеся видом напряжённого состояния конструктивных элементов, будут характеризоваться различными значениями коэффициента силового фактора. На рис. 1 показаны схемы некоторых простых конструкций и значения коэффициентов силового фактора С_к для них [7].

Из физических соображений ясно, что значение C_к не может быть меньше, чем 1,00. Такое его значение имеет конструкция в виде стержня, который передаёт силу P вдоль направления действия силы (рис. 1 а ). Передача силы перпендикулярно к этому направлению сопровождается увеличением коэффициента C_к . Следовательно, можно поставить задачу отыскания наивыгоднейших способов передачи силы как вдоль направления её действия, так и перпендикулярно к нему, – способов, обеспечивающих минимально возможное значение коэффициента силового фактора для этих типовых простейших актов передачи силы. Тогда эффективность силовой работы любой конструкции или её отдельных час-

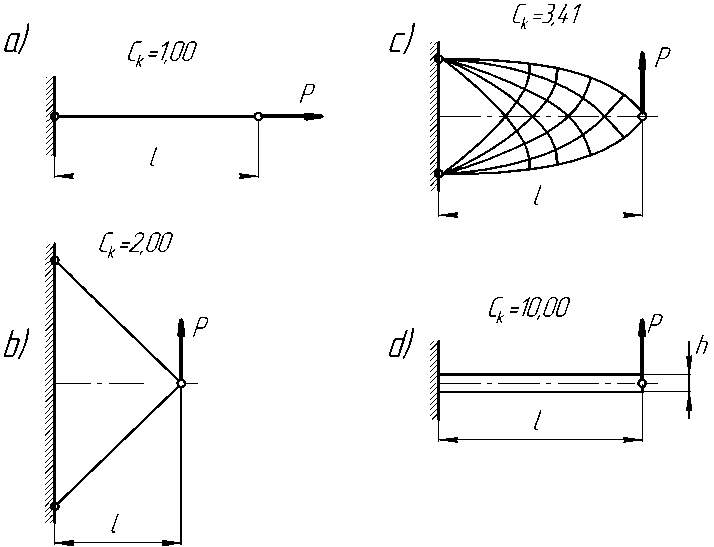
Рис. 1. Схемы конструкций и значения коэффициента силового фактора

тей (элементов) можно оценивать по степени приближения её коэффициентов силового фактора к указанным минимально возможным значениям в типовых (элементарных) условиях. Рассмотрим несколько примеров.

На рис. 2 показаны три варианта конструкции для условий задачи, представленных на рис. 1а. Наряду с решением (рис. 1а) есть не менее эффективная по величине силового фактора конструкция в виде пластинки шириной h и толщи-нойδ, находящейся в одноосном поле погонных усилий (“размазанный стержень”, рис. 2а). Ха- рактерно, что значение Cк не зависит от ширины пластинки h .

Для двухстержневой статически определимой симметричной фермы (рис. 2 б ) значение коэффициента C_к будет интенсивно расти с увеличением угла 2 α между осями стержней. Для соотношения размеров h = l этот угол становится равным 53 градусам, и коэффициент C_к принимает значение 1,249. Для статически неопределимой симметричной трёхстержневой фермы (рис. 2 в ) при одинаковых значениях жёсткостей стержней значение C_к составляет только 1,146, т.е. примерно на 8% меньше. Для вариантов 1 а и 2 а коэффициент C_к принимает значение, равное 1, – это минимальное значение коэффициента силового фактора при передаче силы вдоль направ-

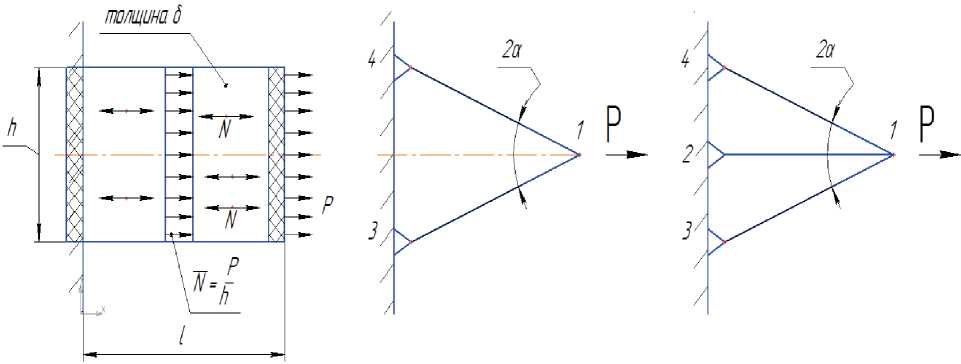
а                         б                         в

Рис. 2. Варианты решения задачи: а – плоская пластинка; б – статически определимая ферма; в – статически неопределимая ферма ления ее действия. Относительную эффективность силовой работы любых конструкций, выполняющих подобные функции, можно оценивать сравнением значений коэффициента Cк для них с единицей.

Обратимся к элементарной задаче передачи силы по направлению, перпендикулярному к направлению действия силы (для краткости будем использовать выражение «в поперечном направлении»). Схема условий задачи показана на рис. 3а: сила Р приложена в т.1 на расстоянии l от опорной плоскости А и направлена параллельно ей. Область, в которой может размещаться конструкция, ограничена размерами l и h (выделена пунктиром).

Очевидно, что передать силу Р на опору по кратчайшему пути – в поперечном направлении – одним шарнирно закрепленным на опоре стержнем невозможно (рис. 3б). Невозможно также выполнить задачу с помощью комбинации стержней, в которой оси стержней ориентированы либо вдоль направления линии действия силы, либо перпендикулярно к ней – такие системы геометрически изменяемы (рис. 3в, 3г). Необходим еще хотя бы один наклонный стержень (подкос), образующий с направлением силы Р угол, отличный от прямого. Некоторые из множества возможных вариантов ферм, осуществляющих требуемую передачу силы Р , показаны на рис. 4.

Оперируя с модулями усилий в стержнях, для вариантов а, б получим следующие соотношения для силового фактора G и коэффициента C_к (в

приведённых соотношениях углы а для каждого варианта конструкции соответствуют показанным на рис. 4; обозначения стержней здесь и далее образованы номерами их узлов).

13             ;     12           ; 13             ;

sin а        tga      cos а ll—2 = 1 .

Силовой фактор

^G = | ^ 1-21 l 1-2 ⁺ | ^ 1 - 31 l i

( 1 = Pl ---+

1      )

vtga sinacosa,'

Коэффициент силового фактора

Ck=Л+——. tga sin a cos a

Если принять h = l и a = 45 0 , то коэффициент C_к получает значение 3,0. Это в три раза боль-

ше, чем при передаче силы стержнем на такое же расстояние вдоль направления действия силы. С использованием соотношения (9) можно отыс-

кать оптимальное значение угла a , соответствующее минимуму коэффициента C_к.

На рис. 4 в показан один из вариантов статически неопределимой фермы. Здесь представляется обширное поле для исследований в оценке эффективности силовой работы вариантов схем ферм и поиске рациональных конструкций, в том числе в случаях одновременного действия сил параллельно опорной плоскости (передача в попе-

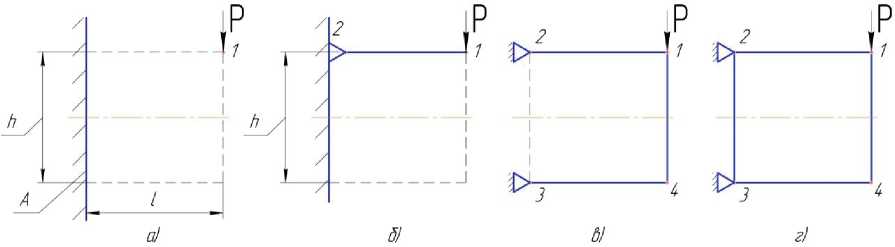
Рис. 3. Задача о передаче силы в поперечном направлении

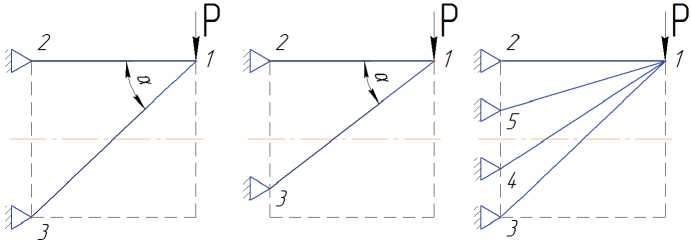
а                   б                     в

Рис. 4. Варианты решения задачи:

а – двухстержневая ферма с подкосом максимальной длины; б – двухстержневая ферма с подкосом меньшей длины; в – статически неопределимая ферма речном направлении) и перпендикулярно ей (передача вдоль направления линии действия силы).

Обратимся вновь к задаче, условия которой показаны на рис. 3а и к конструкции, показанной на рис. 3г. «Неработоспособную» геометрически изменяемую систему из четырех стержней (рис. 3г) можно преобразовать в геометрически неизменяемую силовую конструкцию не за счет введения в нее подкосов, как на рисунках 4 а –4 в , а другим путем: «зашить» образованную стержнями рамку тонкой пластинкой – стенкой толщиной δ (рис. 5 а ). Для простоты рассуждений, но не изменяя сущности явлений, будем считать стержни абсолютно жесткими. Оси стержней после деформации конструкции остаются прямыми, а их длина не изменяется. Края пластинки – стенки, соединенные по всей длине со стержнями, также остаются прямолинейными. Если перемещения узлов 1 и 4 малы (в практике часто бывает именно так), можно принять их линейными вдоль линии действия силы Р (а не дуговыми относительно узлов 2 и 3). Тогда после деформации рамка стержней, зашитая стенкой, примет форму, показанную на рис. 5а пунктирными линиями. Здесь номерами 1' и 4' обозначены узлы 1 и 4 после деформации. При таких условиях пластинка – стенка будет испытывать деформацию чистого сдвига. На рис. 5 б стержни и стенка представлены в расчлененном виде и потоки касательных сил Т . На этом рисунке Т_пл . – поток, с которым стержни действуют на пластинку – стенку; Т_{ст .} – поток, с которым стенка действует на стержни.

В стержнях будут возникать, благодаря их взаимодействию со стенкой, осевые усилия. Очевидно, что в поперечных сечениях этой конструкции проекции осевых усилий в стержнях 1-2 и 43 на направление силы Р равны нулю. Иначе говоря, осевые усилия в этих стержнях не участвуют в уравновешивании внешней силы Р и в непосредственной передаче ее на опору. Здесь внешняя сила передается в поперечном направлении касательными усилиями в пластинке – стенке. Во всех ее сечениях, параллельных стержням, действуют одинаковые потоки касательных сил T=P/h и касательные напряжения τ= T δ. Для оценки эффективности такого способа передачи силы в поперечном направлении проведём сравнение значений коэффициента силового фактора Cк, вычисленного согласно (8) для стенки и рассмотренных выше ферм. Эквивалентное напряжение σэкв вычислим с использованием четвёртой теории прочности [8], выражение для которого в условиях чистого сдвига приобретает вид σэкв = V3τ.              (10)

Тогда силовой фактор пластинки

G= ∫VσэквdV=σэквV=V3τδhl=3δhδhl=V3Pl(11) V                     δh и коэффициент силового фактора

^C k ⁼ 3 ≈ 1,73 .             (12)

Для полученных результатов (11) и (12) отметим два замечательных обстоятельства – вывода. Первое: из (11) следует, что при передаче силы в поперечном направлении стенкой, находящейся в условиях чистого сдвига, величина силового фактора G не зависит от параметра конструкции h , а определяется величиной действующей силы и расстоянием l , на которое передается сила. (Так, например, потребная по условию статической прочности площадь поперечного сечения стенки лонжерона однолонжеронного крыла и ее масса не зависят от строительной высоты лонжерона, т. е. от его размещения вдоль хорды крыла). Коэффициент силового фактора C_к имеет фиксированное значение (1,73), подобно пластинке или стержню, которые передают силу вдоль направления её действия

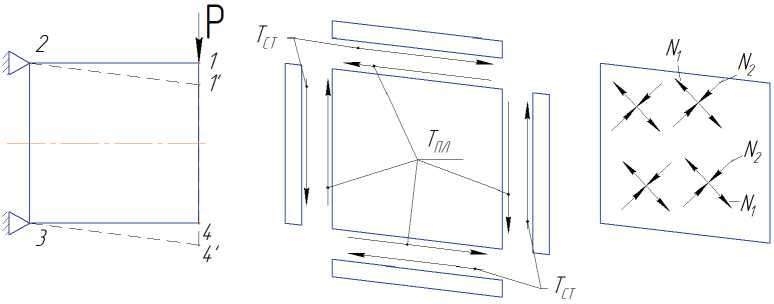
Рис. 5. Деформации и усилия в рамке с тонкой стенкой:

а – исходное и деформированное (пунктир) состояния; б – усилия взаимодействия стенки с окаймляющими стержнями; в – потоки главных усилий в стенке

( C_к =1,00 – рис. 1 а и 2 а ).

Второй вывод можно сделать, сравнивая значения коэффициентов силового фактора для ферм, показанных на рис. 4 , и для рассмотренной нагруженной сдвигом тонкой стенки. Так, для соотношения размеров области h ₌ l нагруженная сдвигом пластинка выгоднее наилучшей двухстержневой статически определимой фермы с одним подкосом (рис. 4 а ), согласно соотношению значений коэффициентов силового фактора, в 3,0:1,73 ≈ 1,73 раза. (Без учёта массы стержней рамки, к ним обратимся далее). Здесь замечательно то, что при уменьшении размера h по отношению к l угол α в вершине фермы, показанной на рис. 4 а , будет уменьшаться, а коэффициент силового фактора, согласно (9) – расти; при этом коэффициент силового фактора тонкой пластинки – стенки будет оставаться неизменным.

Если размер h достаточно велик, то стенка с потребной по условиям прочности толщиной δ может потерять устойчивость при значениях касательных напряжений τ _кр , меньших, чем разрушающее напряжение τ _разр . Работа стенок, потерявших устойчивость при сдвиге, и их взаимодействие с окаймляющими стержнями подробно рассмотрены в литературе (см., например, [9]).

Итак, эффективной (рациональной) конструкцией для передачи силы в поперечном направлении является стенка, работающая на сдвиг. Силовой фактор стенки не зависит от высоты (ширины) стенки, а определяется только величиной действующей силы и расстоянием, на которое осуществляется передача силы; коэффициент силового фактора имеет стационарное значение (при использовании четвёртой теории прочности – 1,73). Возможные осложнения в работе стенки связаны с потерей ею устойчивости. При этом стенка, по всем четырем сторонам соединенная с достаточно жесткими стержнями, полностью работоспособность не утрачивает, но система внутренних усилий в конструкции (механика силовой работы) существенно изменяется [9].

Обратимся теперь к стержням, окаймляющим по всем сторонам стенку (рис. 5 ). Рассмотрим сначала взаимодействие стенки со стержнями 1-2 и 4-3. Схема взаимодействия показана на рис. 6а – 6г.

На рис. 6а показана стенка, нагруженная само-уравновешенными потоками касательных сил (ПКС) Т_пл (обозначение усилий аналогично рис. 5) и стержни 1-2 и 3-4, на которые со стороны стенки действуют ПКС стенки Т_ст . Стержни 1-4 и 2-3 на этом рисунке для удобства не показаны. ПКС Т_ст создают в стержнях 1-2 и 4-3 нормальные усилия соответственно растяжения и сжатия. На рис. 6б показаны участки этих стержней длиной z и действующие на них самоуравновешенные усилия. На рис. 6в показаны эпюры нормальных усилий в стержнях и опорные реакции в узлах ^R 2 ^и R 3 = T ст l . На рис. 6г показана правая отсеченная часть конструкции – рамки с пластинкой и стержнями, на которую действует са-моуравновешенная система сил: внешняя сила Р и внутренние усилия (действие отсечённой левой части конструкции) – нормальные в стержнях 1-2' и 4-3' и ПКС в стенке Т_ст .

Итак, в рассматриваемой комбинированной конструкции стенка передает внешнюю силу Р в поперечном направлении и испытывает деформацию сдвига; стержни 1-2 и 4-3 нормальными усилиями растяжения-сжатия уравновешивают момент, возникающий при передаче силы в поперечном направлении. Стержни 1-4 и 2-3 предназначены соответственно для преобразования сосредоточенной силы P в ПКС в стенке и обратно.

Теперь можно сопоставить значения силового фактора и коэффициента силового фактора

I

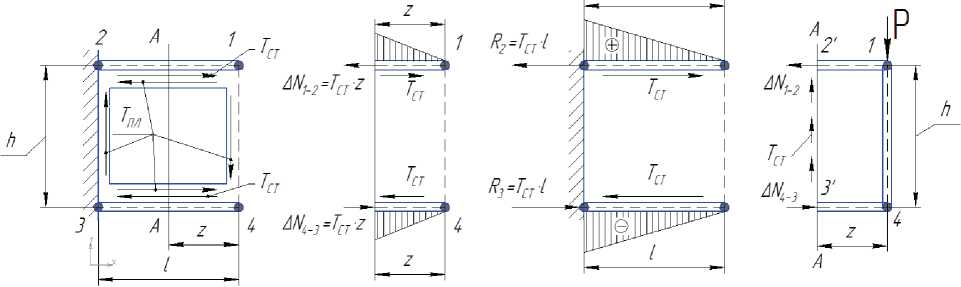
а                        б                   в                   г

Рис. 6. Образование нормальных усилий в стержнях:

а – взаимодействие со стенкой; б – уравновешивание участков стержней; в – эпюры нормальных усилий в стержнях и опорные реакции;

г – уравновешивание участка стенки совместно со стержнями

Таблица 1. Коэффициенты силового фактора фермы и балки в зависимости от удлинения балки l

l 1 2 4 8 16 32 α0 45 26034' 14002' 708' 3034' 1047' C фер мы 3,000 4,501 8,271 16,09 32,02 65,63 С ба лки 3,732 4,232 5,892 9,857 17,79 33,76 в т.ч. С поя сов 1,000 2,000 4,000 8,000 16,000 32,00 С стоек 1,000 0,500 0,250 0,125 0,0625 0,0312 С ст ен ка 1,732 1,732 1,732 1,732 1,732 1,732 С фермы C балки 0,693 1,064 1,398 1,632 1,800 1,944 всей конструкции в виде комбинации стенки и окаймляющих ее стержней по соотношениям (3) и (8) соответственно. В каждом стержне нормальные усилия линейно изменяются по длине стержня от нулевого до максимального значения. При соотношении размеров l/h=1 максимальные усилия в стержнях достигают величины внешней силы Р. Тогда силовой фактор всех четырех стержней составит Gст = 4 х 0,5 х |Р| х l = 2 |P| l. Силовой фактор всей конструкции принимает значение G^ = Gcmeнки + Gcm = 1,73Pl + 2Pl = 3,73Pl, а стенки ст коэффициент силового фактора Ck = 3,73 .

Это значение больше, чем для ^Σ наилучшей фермы с подкосом (рис. 4 а ) в 3,73/3,0 ≈ 1,24 раза.

Соотношение значений коэффициента силового фактора стержневой конструкции – фермы и комбинации тонкой стенки и стержней – поясов (1-2, 2-3) и стоек (1-4, 3-2), т.е. балки, будет изменяться в зависимости от параметра l/h . Обозначим его l и будем называть далее удлинением балки. Запишем расчетные соотношения для составляющих силового фактора фермы и балки. Для этого воспользуемся рис. 7.

Коэффициент силового фактора фермы будем вычислять по выражению (9).

Составим выражение для коэффициентов силового фактора элементов балки и просуммируем их.

Для стенки согласно (12) C k = V3 = 1,73.

Для двух стержней – поясов 1-2 и 3-4

2

поясов            ^, ст                              ,

h тогда коэффициент силового фактора для поясов

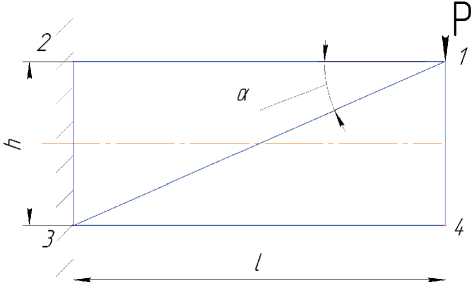
Рис. 7. Подкосная ферма и балка, вписанные в область с размерами l и h

тогда коэффициент силового фактора стоек

C = G — ^k стоек       ст _Pl

h = 1

l " l'

В результате расчетные соотношения для коэффициентов силового фактора подкосной фермы, составленной из стержней 1-2 и 1-3 на рисунке 7, и балки, ограниченной отрезками, проходящими через точки 1-2-3-4 на том же рисунке, приобретают следующий вид.

Ферма из двух стержней 1-2 и 1-3, согласно (9):

Cg = Л + tgα

1sinαcosα

Балка в целом

C k

поясов

= l .

Для двух стоек 1-4 и 2-3 силовой фактор

2

стоек           ^, ст                              ,

h

C_k = C + C + C « 1,73 + 1 + ¹ . (13) балки стенки поясов стоек _l

Численные значения величин, полученные по соотношениям (9) и ( 1 3) для некоторых значений удлинения балки l приведены в табл. 1.

Анализ приведенных в табл. 1 значений позволяет сделать некоторые выводы. Я с но, что при малых значениях удлинения балки l (не более

чем ~2) выгодно передавать силу в поперечном направлении ферменной конструкцией с рациональной схемой стержней. В области значений l около 2,0 ферменная и балочная конструкции конкурируют по потребному объему материала и массе конструкции. В реальных условиях в этой области значений l результат сравнения этих вариантов конструкции в большой мере будет зависеть от мастерства конструктора и других условий – ограничений, в том числе, например, технологических. При значениях l от нескольких единиц и более передача сил в поперечном направлении тонкостенной балкой приобретает неоспоримое преимущество перед использованием для этой цели двухстержневой подкосной фермы.

Ясно также, что с ростом значения удлинения балки l растет доля поясов в общей величине коэффициента силового фактора балки и уменьшается доля стенки и стоек. Подчеркнем, что при этом абсолютное значение коэффициента силового фактора стенки остается постоянным.

Эффективность силовой работы фе р менной конструкции при больших значениях l можно повысить путём более полного использования строительной высоты h заданной области, если подкос 1-3 (рис. 7 ) заменить некоторой «решеткой» стержней.

В летательных аппаратах конструкции, состоящие из стержней и плоских или искривленных тонкостенных элементов, эффективно выполняют задачи передачи внешних сил вдоль направления линии действия силы и (или) в поперечном направлении. Принципиально теми же элементами, работающими либо на сдвиг, либо на растяжение или сжатие, может быть осуще- ствлена передача крутящего момента, действующего относительно какой-либо оси. Из строительной механики тонкостенных конструкций известно, что эффективные конструкции для передачи крутящих моментов представляют замкнутые тонкостенные контуры – тонкостенные оболочки (рис. 8). На этом рисунке: Мкр – крутящий момент; δ – толщина оболочки; l – длина оболочки (расстояние, на которое передается крутящий момент); Ω – площадь фигуры, ограниченной замкнутым контуром поперечного сечения оболочки; Т – поток касательных усилий в тонкостенном контуре поперечного сечения оболочки. Если толщина оболочки значительно меньше размеров контура, ограничивающего её поперечное сечение, поток касательных усилий Т определяют по формуле Бредта

T =

M кр

2Ω

Для оценки эффективности силовой работы такой конструкции подсчитаем значение силового фактора и коэффициента силового фактора оболочки, показанной на рис. 8. Материал оболочки во всём её объеме находится в условиях сдвига с касательными напряжениями

Т М кр τ==

δ2Ωδ

.

Эквивалентные напряжения при сдвиге, как и ранее, σ _экв = л] 3 τ . Объем материала оболочки экв

V=Fсечl=δПl, где V – объем материала оболочки; Fсеч – площадь, П – периметр поперечного сечения оболочки.

Тогда значение силового фактора Gоб.кр тонкостенной оболочки с замкнутым контуром площадью Ω и толщиной оболочкиδ, которая передаёт крутящий момент Мкр на расстояние l, опорная плоскость

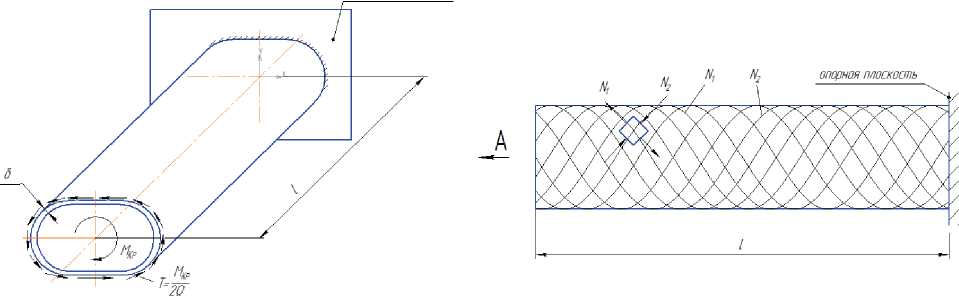
а                                                  б

Рис. 8. Кручение тонкостенной оболочки: а - схема нагружения; б - потоки главных усилий (ПГУ)

вычислим согласно выражению

G_o6 - = f ^ dV = ^, V = V3 Mds П = 0, 5^ mi П . (16) об . кр экв экв _{2Ω δ} кр _Ω

Из этого выражения видно, что меньшие значения силового фактора при прочих одинаковых условиях будут иметь оболочки с меньшими отношениями периметра к площади контура. Потребный объем и масса конструкции будут тем меньше, чем меньше это отношение. Известно, что это отношение минимально для окружности и ограниченного ею круга. Иначе говоря, наилучшей конструкцией для передачи крутящего момента является тонкостенная оболочка с круговой формой поперечного сечения.

Для того, чтобы получить выражение для коэффициента силового фактора С_{kоб . кр} при передаче тонкостенной оболочкой с замкнутым контуром крутящего момента М_кр на расстояние l , необходимо определить характерную внешнюю силу и характерный линейный размер конструкции. За линейный размер конструкции (напомним, он должен определять направление и путь передачи характерной силы) естественно принять длину оболочки l . Для определения характерной силы представим внешний крутящий момент как результат действия пары сил Р_r с плечом, равным площади контура W в степени Ѕ, и в качестве характерной силы возьмём одну из составляющих этой пары:

Р - Мкр r Ω1/2 .

Тогда из (8) с учётом (16) выражение для коэффициента силового фактора в рассматриваемых условиях приобретает вид

С об.кр

3 П

_{2 Ω} 1/2 ^.

Для оболочки с круговой формой поперечного сечения диаметром D периметр П = nD , а площадь контура Q — —nD2. Подставив эти

4

выражения в формулу (17), получаем, что значение коэффициента силового фактора цилиндрической тонкостенной оболочки с круговой формой поперечного сечения, нагруженной крутящим моментом, составляет 3,069, т. е. имеет стационарное значение и не зависит от диаметра оболочки.

Механика силовой работы тонкостенной оболочки при кручении принципиально аналогична работе стенки при передаче силы в поперечном направлении (перерезывающей силы в тонкостенной балке). ПГУ в оболочке (N1 и N2) представляют собой винтовые линии с углами подъема ± 45o к оси оболочки, как показано на рис. 8б.

Получены стационарные значения коэффициентов силового фактора элементарных конструкций, обеспечивающих наивыгоднейшую передачу внешних нагрузок в трёх типовых проектных задачах: передача силы вдоль направления действия силы; перпендикулярно к этому направлению; передача крутящего момента. При проектировании или анализе конструкций эффективность их силовой работы в подобных задачах может оцениваться сравнением значений коэффициентов силового фактора конструкций или их частей с приведёнными стационарными значениями.

• 1.    Шейнин В.М., Козловский В.И. Весовое проектирование и эффективность пассажирских самолетов. М.: Машиностроение, 1984. 552 с.

• 2.    Комаров В.А. Весовой анализ авиационных конструкций: теоретические основы // Общероссийский научно-технический журнал “Полет”. 2000. №1. С. 31-39.

• 3.    Комаров А.А. Основы проектирования силовых конструкций. Куйбышев: Куйбышевское книжное изд-во, 1965. 88 с.

• 4.    Комаров В.А. Проектирование силовых схем авиационных конструкций //Актуальные проблемы авиационной науки и техники. М.: Машиностроение, 1984. С. 114-129.

• 5.    Петренко С.А., Штанько Е.Д. Оценка перспективности вариантов силовой конструкции моноблочных ракет и качества принимаемых конструкторско-технологических решений // Общероссийский научно-технический журнал «Полет». 2001. № 9. С. 46-49.

• 6.    Весовое проектирование летательных аппаратов на основе дискретных математических моделей / Д.М. Козлов, В.А. Комаров, В.Н. Майнсков, О.Н. Попов, Г.А. Резниченко // Техника воздушного флота. 1999. № 4-5. С. 31-37.

• 7.    Комаров В.А., Гуменюк А.В. Критерий силового совершенства конструкций крыльев // Общероссийский научно-технический журнал «Полет». 2003. № 6. С. 24-30.

• 8.    Беляев Н.М. Сопротивление материалов. М.: Глав-

  ная редакция физико-математической литературы 9. Кун П. Расчет на прочность в самолетостроении. М.: изд-ва «Наука», 1976. 608 с.                               Оборонгиз, 1961. 306 с.