Об оценке наблюдаемости температурного поля слябов при нагреве в методических печах

Постановка задачи

При нагреве металла в промышленных печах для непосредственного измерения доступна только температура его поверхности, причем определена она может быть, к сожалению, с достаточно ограниченной точностью. Температуры внутренних точек так же, как и среднемассовая температура, принципиально не могут быть измерены инструментальными средствами, определяются они расчетным путем, либо прямо по математической модели, настроенной на реальный процесс, либо по разработанным на её основе алгоритмам контроля. В связи с этим при построении автоматизированных систем управления технологическими процессами (АСУ ТП) нагревательных печей возникает задача разработки приемлемых алгоритмов оценки температурного поля заготовок по доступным для измерения величинам процесса. Решение этой задачи необходимо, во-первых, для создания замкнутых систем управления с обратной связью по температуре нагреваемого металла, во-вторых, для оценки начального температурного поля заготовок, сажаемых в печь, так как вследствие неконтролируемости условий нагрева и охлаждения металла перед посадом в печи оно, как правило, неизвестно. Разработка и внедрение подсистемы оценки начального температурного поля заготовок позволит получить максимум эффекта от оптимального управления особенно первыми по ходу металла зонами нагрева, так как величина эффекта напрямую связана с точностью оценки начальной температуры металла.

Важность оценки начального температурного поля заготовок подчеркивается и в зарубежных публикациях [1, 2].

В-третьих, важным достоинством положительного решения такой задачи будет

вполне обоснованный вывод о том, что температурное поле заготовок принципиально может быть оценено по результатам только текущих измерений и совершенно независимо от предыстории нагрева. Следовательно, непрерывный контроль температуры металла по ходу нагрева не является, в принципе, абсолютно необходимым для того, чтобы иметь возможность определять температурное поле заготовки в какие-то ответственные моменты времени.

Выясним принципиальную возможность такой оценки, т. е. рассмотрим задачу оценки наблюдаемости процесса нагрева в смысле, определяемом в работах [3–7].

Математическое описание процесса

Следуя, например, работам [8–11], опишем процесс нагрева металла в печи полностью линеаризованным уравнением теплопроводности

∂ t ( x , τ )     ∂ ² t ( x , τ )

=a        , 00(1)

∂τ          ∂x2 ,, с начальным

t(x,0)=t0(x),0≤x≤L(2)

и граничными условиями:

∂t(0, τ) =0,τ≥0;(3)

∂ x

λ ∂t(L,τ) =α[tП(τ)-t(L,τ)],τ≥0,(4)

∂ x

где t ( x , τ ) – температура в точке с пространст-

венной координатой x в момент времени τ ; a и λ – соответственно коэффициенты температуропроводности и теплопроводности; L – расчетное сечение заготовки (обычно половина ее толщины); t ⁰( x ) – некоторая функ-

ция, описывающая начальное температурное

поле заготовки; а - коэффициент теплоотдачи для обогреваемой поверхности металла; t П ( т ) = и ( т ) — температура рабочего пространства печи, являющаяся управляющим воздействием и ( т ).

Используя известный метод прямых [12, 13], преобразуем уравнение теплопроводности (1) в систему обыкновенных дифференциальных уравнений dt a dt = 52( t 2- t');

dt ₂    a

"Т" = TI⁽ t 1 ^{- 2} t 2 + t 3^);

d т   52

;

^dt n - 1

a d т dtn d т

2⁽ t n - 2 ² t n - 1 + t n ^);

a 8       4

= „2 С, t ПОВ + т t n - 1 ⁴ t n ).

5 3        3

Здесь t_t ( т ) - температура в центре i -го слоя заготовки; t ПОВ = t ( L , т ) - температура ее поверхности; 5 - толщина расчетного слоя, i = 1 для центрального слоя заготовки: центр сляба находится в середине центрального слоя; n – номер слоя, выходящего на поверхность заготовки, т. е. правая граница слоя является поверхностью заготовки, при этом вполне понятно, что число слоев, на которое условно разбито расчетное сечение заготовки, должно быть нечетным: в этом случае центр заготовки будет располагаться в центре центрального слоя. Расчетная схема заготовки приведена на рисунке.

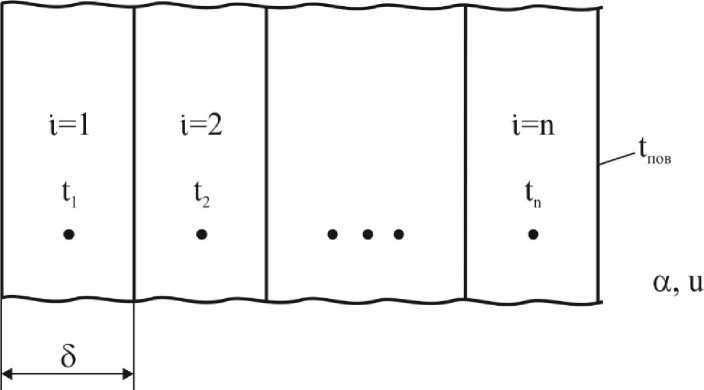
Расчетная схема сляба Calculation scheme of a slab

Для приведения математического описания к стандартному для теории наблюдаемости виду исключим из системы (1) температуру поверхности заготовки t _ПОВ (считается, что переменными состояния объекта управления являются только температуры центров расчетных слоев), для этого проведем пространственную дискретизацию граничного условия нагрева (4):

X

t ПОВ t n

5/ 2

= ^{a (} u t ПОВ ) ^ t ПОВ =

a        2X—:-----и +-------1„.2X/5 + a   2X + a5 n

С учетом этого система (5) перепишется в виде dt a .

-7¹ = тг( t 2 — t i);

d т 52

dt 2 a

"Г" = T2"⁽ t i ^{— 2} t 2 ⁺ t 3^);

d т 52

;

^dt n — 1

d т dt_n d т

a

2⁽ t n — 2 ² t n — 1 ⁺ t n ^);

a _r8     a5 4 „_z2    2X        ,

= -y[--- U + tn -l+4(----1) tn ].

52 3 2X + a5    3 n 1   3 2X + a5

Дополним систему (7) «уравнением наблюдения» [3], получающимся при уже упомянутой пространственной дискретизации граничного условия нагрева, записанного в форме закона Ньютона:

_ a t пов =

2X/o + a

2Х

U +---------- tn .

2X + a5 n

Вполне понятно, что температура поверхности заготовки t ПоВ = t ( L , т ) здесь играет роль наблюдаемого выхода объекта управления [3–7].

Матричное описание объекта, как это хорошо известно [3–7], принято представлять следующим образом:

dt

— = At + Bu; d т

t пов = Ct + Du, где t = (t1, t2, .., tn)T - вектор-столбец температур центров расчетных слоев, верхний индекс «Т»

означает транспонирование; А и B n -мерный вектор-столбец управлений;

матриц А , B , С и D приведены ниже.

–

матрицы размером n х n ; и = (0 0 ... u )^т

С и D –

–

матрицы-строки размером n ; конкретные виды

A =

² a

" 62

a

—

a

2 ^a

к

a

;

k

( 0

4 a

4Х

₄ a ₍

5 ² 3(2 X + a5 )

—

1) ^

B =

;

к

⁸ a ^a

35(2X + a5),

C = 1 0

2Х

2X + a5j’

D = 1 0

а52Х + «5

.

Оценка наблюдаемости температурного поля

Провели исследование наблюдаемости для различных конкретных значений n , во всех рассмотренных нами случаях получали, что ранг соответствующей матрицы наблюдаемости был равен порядку объекта управления, так, например, для n = 3 матрица наблюдаемости имеет вид

( C T

4 а р 3 5 ²

в

V

ур

Здесь р =

2 Х

2 Х + «5’

A ^T C ^T

( A T )² C T ) =

4 а ²р

\

^{( -}

3 5 ⁴ 8 a ²  4 a

50 4" ⁺ 3 5 2 ^{7 ) Р}

.

(4£ + Y 2 ) Р

3 5

4 Х

a

Y = 4—(

5 ² 3(2 Х + «5 )

^- 1).

Нетрудно видеть, что определитель данной л     16а3Р3 п матрицы равен А =---— * 0, т. е. всегда не равен нулю, следовательно, ранг матрицы наблюдаемости r = n = 3 и система вполне наблюдаема [3–7]. Таким образом, можно сделать вывод, что процесс нагрева слябов в печах вполне наблюдаем, т. е. температурное поле в заготовке в момент времени т = 0: t(x, 0) = t0 (x) может быть однозначно опреде- лено по данным измерения температуры ее поверхности и температуры рабочего пространства печи на некотором конечном последующем отрезке времени.

При этом следует иметь в виду, что при оценке температуры металла по наблюдаемым (измеряемым) величинам процесса нагрева неизбежно запаздывание информации о неизвестном температурном поле заготовок, так как это поле определяется для левого конца отрезка наблюдения, поэтому этот метод целесообразнее всего использовать для определения начального температурного поля слябов горячего посада при их нагреве в методических печах. В этом случае не может быть нанесен какой-либо ущерб процессу управления из-за запаздывания, так как первые по ходу металла методические зоны печей не управляемы, заготовки в них нагреваются теплом отходящих продуктов сгорания. В принципе же метод может быть использо- ван и в других случаях, важным его достоинством является то, что температурное поле заготовок оценивается только по результатам текущих измерений совершенно независимо от предыстории нагрева.

Разработка и исследование конкретных алгоритмов оценки

Задача об определении температурного поля 1 ⁰( x ) по функции управления и ( т ) и результатам измерения температуры поверхности металла на некотором отрезке времени относится к ретроспективным обратным задачам теплопроводности [14, 15] и является некорректно поставленной [15, 16]. Как это хорошо известно, задача решается при использовании дополнительной информации об искомом решении [15, 16], т. е. методом регуляризации.

В работе [10] был опробован алгоритм оценки для случая, когда как искомое, так и используемое при решении задачи температурное поле металла аппроксимировалось конечно-разностной схемой и задача напрямую решалась в таком конечно-разностном представлении, однако проведенные вычислительные эксперименты не дали приемлемых результатов, погрешность оценки t ⁰( x ) оказалась недопустимо большой. Часто получали нереальный профиль оцениваемого температурного поля. В связи с этим для решения задачи применили следующий регуляризирую-щий подход.

Известно [17], что температурное поле слябов при нагреве в печах удовлетворительно аппроксимируется многочленом второго порядка, поэтому, приняв такое допущение, можно свести задачу об определении t ⁰ ( x ) к нахождению неизвестных численных значений параметров (коэффициентов) этого многочлена.

Эту задачу – задачу определения параметров многочлена – решали как методом наименьших квадратов, так и методом наименьших модулей, причем моделирование показало, что разработанные алгоритмы являются практически равноценными. В процессе исследования установили, что точность оценки t0 (x) по данным алгоритмам существенно зависит от точности информации о температуре поверхности заготовки на отрезке наблюдения. Данные о влиянии погрешно- стей измерения температуры поверхности на погрешность оценки t0(x) приведены в работе [10]. Показано, что если считать, что погрешность определения температурного поля в каждой точке представительного сечения заготовок должна быть не больше 25 град., то погрешность измерения температуры поверхности металла в печи на отрезке наблюдения должна быть достаточно малой и не превышать 10 град., если же это требование пре-дьявлять только к среднемассовой температуре нагреваемого металла, то предел допустимой погрешности измерения может быть повышен до 15 град. При этом выяснили также, что наибольшее влияние на точность оценки температурного поля оказывает погрешность измерения температуры поверхности в начале наблюдения, чем в последующие моменты времени, в этом проявляется известный принцип независимости поведения реальных физических систем от начальных данных при достаточно большом τ .

Если рассматривать задачу оценки начального температурного поля слябов горячего посада при посаде их в методические печи, то допустимая погрешность измерения температуры поверхности слябов может быть повышена до 20 град. Объясняется это тем, что ошибка определения начальной среднемассовой температуры металла в 30 и более град. практически уже через 10 мин не сказывается на точности расчета температурного поля. Длительность же нагрева слябов в неотапливаемых методических зонах в любом случае больше этого времени, следовательно, к моменту начала управляемого процесса нагрева погрешность расчета температурного поля металла, обусловленная неточностью оценки начальной температуры, будет незначительной.

В работе [18] проведены исследования по оценке температуры металла многочленом нулевого порядка, иначе говоря, некоторым числом, характеризующим все температурное поле – среднемассовую температуру. Данные исследования дополняют результаты работы [10], причем разработанный алгоритм выгодно отличается от алгоритма [10] с точки зрения количества необходимых вычислений. Последнее достаточно важно при построении АСУ ТП, работающей в реальном масштабе времени.

Влияние погрешностей измерения температуры поверхности на точность оценки среднемассовой температуры приведено в работе [18].

Выводы

Рассматривается задача оценки наблюдаемости температурного поля слябов при их нагреве в методических печах. Установлено, что объект вполне наблюдаем, т. е. температурное поле заготовки в некоторый момент времени может быть однозначно определено по данным измерения температуры поверхности и температуры рабочего пространства на некотором последующем отрезке времени, т. е. непрерывный контроль температуры по ходу процесса нагрева с самого его начала не является в принципе абсолютно необходимым. Приводятся конкретные алгоритмы решения задачи. Результаты работы могут быть использованы при построении автоматизированных систем управления методическими нагревательными печами.