Об оценке точности формы листовых деталей, выполненных из композиционных материалов, с помощью гауссовой кривизны

Информационной основой совершенствования ТП может стать анализ точности геометрии путём статистической обработки измеренных действительных геометрических параметров изделий и их соответствия идеальному геометрическому прототипу. Под точностью ТП здесь будет пониматься величина погрешности действительной формы изделия относительно идеального геометрического прототипа. Под стабильностью ТП понимается обеспечение постоянства распределения вероятностей действительных значений геометрических параметров в течение определённого временного интервала в рамках неизменного ТП.

Содержание статистического анализа носит универсальный характер и не требует специализированной регламентации. Другое дело – выбор параметров, характеризующих геометрический образ детали. Например, форму листов обшивки корпуса принято характеризовать радиусом поперечного и продольного изгиба, стрелками продольной и поперечной погиби [2]. Такое многообразие параметров, характеризующих форму, препятствует формализации данных о геометрии, снижают эффективность статистического анализа. Оптимальным вариантом оценки точности изготовления формы может стать аналитическое моделирование оцениваемой поверхности [3]. В этом случае обеспечивается приемлемая информативность анализа, появляется возможность оперирования абсолютными или относительными значениями геометрических характеристик формы и проведения сравнительного анализа точности формы деталей, имеющих различную конфигурацию.

Рассмотрим вариант оценки отклонения поверхности листовой детали от плоскости с помощью таких параметров дифференциальной геометрии, как гауссова (полная) K и средняя (эйлерова) Н кривизны [4]. Для их расчёта через нормаль в заданной точке поверхности проводят всевозможные плоскости, сечения поверхности которыми являются нормальными сечениями, а кривизны нормальных сечений – нормальными кривизнами поверхности в этой точке. Максимальная и минимальная из них становятся главными кривизнами k1 и k2. Тогда величина гауссовой кривизны равна K=ki-k2, а средней кривизны Н=1/2(k1 + k2). Если К=0 и Н=0 во всех точках поверхности, то поверхность представляет собой плоскость. Главные кривизны k1 и k2 при описании поверхности векторнопараметрическим уравнением:

r = r(u, v) = x(u, v)i + y(u, v)j + z(u, v)k находятся как корни уравнения:

( EG - F ² ) k ² - ( EN + LG - 2 FM ) k + LN - M ² = 0

где

E = E ( u , v ) = r u . r u ;

_   dr _d r = — r = u ,v оu

F = ^{F ( u}, v ) = r u . r ;

G = G ( u , v ) = r v Jr

L = L ( u , v ) = nr uu

r uu r u r v ;

V EG - F² ’

M = M ( u, v ) = nr_uv

r uv r u r v ;

EG - F² ’

N = N ( u, v ) = nr vv

r vv r u r v     ;

a] EG - F² ’

n- единичный вектор нормали к поверхности.

В неособых точках E>0, G>0, EG-F2>0. Гауссова кривизна поверхности:

K = k 1 k 2

LN - M² .

EG - F² ;

Средняя кривизна поверхности:

k 1 + k 2 EN - 2 FM + GL

H =-----= 7-----TT—

2       2 ( EG - F ² )

Для идентификации формы поверхности детали по значению К существует следующая классификация геометрических примитивов: - К=0, форма детали нулевой гауссовой кривизны идентифицируется как геометрический примитив – плоскость;

• -    К > 0, форма детали положительной гауссовой кривизны: - сфера, эллипсоид, эллиптический параболоид;

• -    К < 0, форма детали отрицательной гауссовой кривизны – гиперболический параболоид.

На практике чаще всего встречаются детали, состоящие из фрагментов различных типов гауссовой кривизны. Рассмотрим технологические шаги оценки формы детали, поверхность которой описаны, как минимум 2 геометрическими примитивами. Источником первичной информации должно стать координатноизмерительное устройство, благодаря которому при обмере детали получают координаты точек, количество которых зависит от заданного шага измерения. Результаты обмера формируются в виде двумерных массивов x i,j =i, y i,j =j с элементами в виде координат z i,j . Индексы массива принимают значения натуральных чисел от начального индекса до конечного. При уменьшении шага между узлами ячеек точность моделирования поверхности возрастает с одновременным увеличением трудоемкости и объема вычислений.

На первом этапе учитывается относительный угловой поворот поверхности, зафиксированной через контактную площадку 3 детали 1 на горизонтальной базовой плоскости 2, см. рис. 1. Т.к. поверхность детали наклонена к горизонтальной плоскости, то точка на верхнем краю, например, с координатой, условно обозначаемой z 1 , может оказаться выше точки с координатой z 2 на пике выпуклости. Для решения этой проблемы поверхность детали аппроксимируется плоскостью, а затем из каждой точки поверхности вычитается значение аппроксимирующей функции в данной точке. Такая операция позволяет сгладить «неровности» и ложные экстремумы через учёт относительного поворота, (см. рис. 2). При этом нахождение максимумов, например, z ' ₂ происходит с точностью не ниже шага разбиения сетки массива.

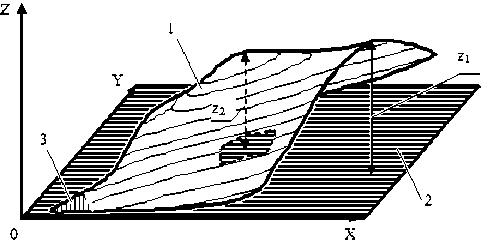
Рис. 1. Положение детали при первичном замере координат точек поверхности: 1 – деталь из КМ, 2 – базовая горизонтальная плоскость; 3 – контактная площадка детали (условно выделена штриховкой)

Далее, выровненная поверхность описывается несколькими геометрическими примитивами на основе локальной аппроксимации соответствующих фрагментов детали. Для выделения фрагментов может быть использован, например, метод граничных ребер. На рис. 3 представлен пример локальной аппроксимации поверхности детали из КМ с помощью двух геометрических примитивов: эллиптических параболоида и цилиндра.

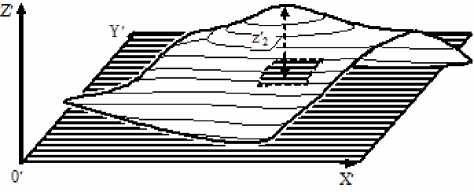
Рис. 2. Положение детали после учёта относительного угла поворота

Рис. 3. Аппроксимация поверхности детали геометрическими примитивами: 1 – эллиптический параболоид, 2 – эллиптический цилиндр

Предлагаемый критерий оценки соответствия поверхности идеальному геометрическому прототипу по гауссовой кривизне носит практически универсальный характер и может быть использован для проведения статистического анализа качества ТП изготовления детали из любого материала и формы. Обязательным условием рассмотренного подхода является использование современных координатноизмерительных устройств, позволяющих формировать двумерные массивы заданных размеров.