Об одной качественной методике оценки рисков целесообразности инвестирования в различные моменты времени

Введение. Основная характеристика инвестиционного проекта - финансовый поток расходов и доходов. Этот поток представляет собой модель предполагаемого потока платежей по проекту и строится на основе совокупности прогнозных оценок на время реализации проекта. Инвестиционный проект, рассматриваемый в условиях определенности, описывается своим чистым денежным потоком R о , R 1 , R 2,..., R n в моменты времени t = 0, 1 1 , 1 2 ,., t n соответственно, где 0 <  1 1 <  1 2 < .< t n = T . Начало проекта t = 0 - момент вложения исходной инвестиции в размере I , T - срок проекта [3].

Для оценки эффективности инвестиционного проекта используют четыре показателя [3], основанные на дисконтировании членов финансового потока проекта к моменту t = 0:

• •    чистая современная стоимость проекта ( net present value , NPV);

• •    внутренняя норма доходности ( internal rate of return , IRR );

• •    срок окупаемости ( discounted payback period , DPP );

• •    индекс доходности ( profitability index , PI ).

Каждый из показателей - это результат сопоставления современных стоимостей инвестиций в проект и отдач от инвестиций. Для дисконтирования членов финансового потока проекта применяется процентная ставка r . Остановимся на показателе NPV.

Соотношение для NPV имеет следующий вид:

NPV = -1 +

N

X i=1

С i

(1 + ri)i

где I – стартовый объем инвестиций; N – число плановых интервалов (периодов) инвестиционного процесса, соответствующих сроку жизни проекта; С i – оборотное сальдо поступлений и платежей в i-м периоде; r i – ставка дисконтирования, выбранная для i-го периода с учетом оценок ожидаемой стоимости используемого в проекте капитала.

Один из самых удобных способов учесть риски по проекту – отразить их уровень в ставке дисконтирования, которая применяется в расчетах показателей экономической эффективности проекта (NPV, IRR, PI, DPP). Для этих целей, по мнению автора, наиболее подходящим является кумулятивный метод расчета, позволяющий выявить различные факторы риска путем использования методологии теории нечетких множеств и прогнозирования по методу числовых рядов.

Пусть r – ставка дисконтирования, %. Ставка состоит из двух частей r = rc+ rf,                                                                           (2)

где   r c – безрисковая ставка доходности, %;

r f – поправка (премия) на риски, %.

В качестве безрисковой ставки обычно используют среднегодовое значение доходности ценных бумаг, соответствующих инвестиционному проекту по срокам и валюте. Например, если предполагаемая валюта инвестиций доллары, то во внимание принимается ставка доходности казначейских облигаций США, срочность которых примерно соответствует сроку инвестиций. Также за безрисковую ставку доходности можно принимать доходность по долгосрочным облигациям правительства РФ, по депозитам Сбербанка, а также по иностранным государственным ценным бумагам со сроком погашения 10–20 лет. Рекомендуют использовать доходность по долгосрочным рублевым депозитам Сбербанка, на начало текущего года она составляла от 5,25 до 12%.

Однако, по мнению автора, первоначальным этапом управления рисками инвестиционного проекта является выбор оптимального момента начала его реализации, то есть момента инвестирования капитала. Таким образом, задача управления риска будет сводиться к прогнозированию и оценке ряда факторов, влияющих на будущую эффективность инвестиционных вложений. Причем количество этих факторов должно быть по возможности минимальным. Для реализации вышесказанного предлагаем использовать метод числовых рядов [1], а в качестве факторов следующие два индекса: Dow Jones и USDX.

Методика оценки риска целесообразности инвестирования в различные моменты времени на основе метода числовых рядов (МЧР) по индексу Dow Jones

Риском мы будем называть вероятность ущерба при вложении средств в инвестиционный проект в выбранном временном интервале.

Риск в случае возрастающего тренда будем оценивать по следующей формуле:

k

Risk = Pin = I -X a,(3)

i = 1

k где Xai = Sk — частичная сумма нормированного числового ряда X ai = 1, который будем интерпрети-i=1

ровать как сумму вероятностей событий, образующих полную группу обобщенного пуассоновского процесса, эффективно моделирующего выбранный индекс ( x_i ) в терминах [1].

При этом подбор числового ряда будет осуществляться по МЧР k-1

<1; k ) = X a im ; p ) x t - i + 1 ,                                    (4)

i= 0

где х_{ - рассматриваемый индекс; y mk ) - модельное значение x i ; m - номер нормированного числового ряда из базы рядов [1]; k - порядок модели, верхний индекс ( m ; k ) - указывает на номер ряда и на порядок модели.

Ошибку построения модели будем оценивать так [1]

t — 1

Д = t -1 й

xi

\

y ( ^{m ; k} ) ^ ²

^xi      J

Рассмотрим индекс Dow Jones c возрастающей динамикой в период начала оживления деловой активности с 09.03.2009 по 22.03.2010.

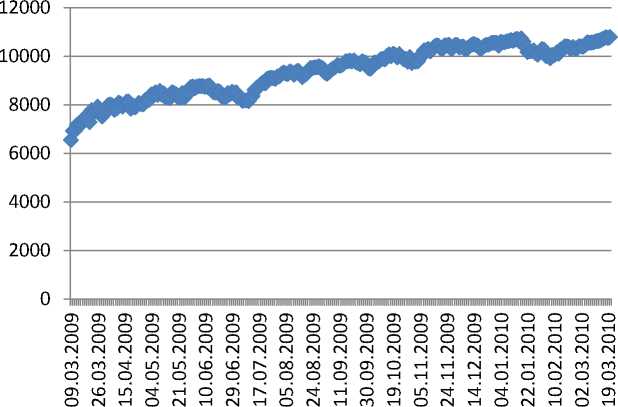
Рис. 1. Индекс Dow Jones с 09.03.2009 по 22.03.2010

Используя метод числовых рядов, аппроксимируем данную динамику, выбрав порядок модели авторегрессии и структуру числового ряда по минимальной ошибке.

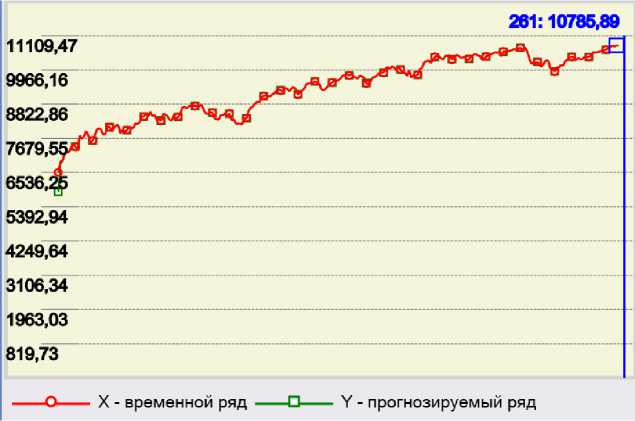
Рис. 2. Визуализация расчетов индекса Dow Jones с 09.03.2009 по 22.03.2010

Расчеты показали, что с минимальной ошибкой Д = 0,0231 , или Д = 2,31% , лучшим будет знако-

“ 9    9    9     9

положительный нормированный числовой ряд ^ — i = — + j^ + Jqqq + ” ‘ • При этом порядок модели

(длина числового ряда, используемая для аппроксимации) равен 17 значениям.

Разобьем исходный ряд данных на 17 примерно равных промежутков по 15–16 значений, преобразовав исходный индекс в кусочно-линейную функцию. Первый промежуток будет с 09.03.2009 по 30.03.2009. Для каждого из этих промежутков можно определить величину риска, согласно формуле (1). Так, риск для первого промежутка будет:

Risk = P in = । - Z = 1 — i = 1 10 '

99  99

--1---I---+ • • •

10 100 100010

« 0 .

Второй промежуток с 31.03.2009 по 24.04.2009, риск будет

Risk₂ = P_In = 1 -У — = 1-- +----+---- «    .

² In     ^io i      100 1000    1016    10

В последующие промежутки риск растет незначительно. Последний промежуток 01.03.2010 по 22.03.2010, риск в этот промежуток составит

¹⁷ 9        Г 9

« 1 .

Risk ₁₇

= P in

^Z = ^{1 -}    17

i = 17¹⁰        L ¹⁰

(71(7)0)0)0)0)0)0)0)0) OOOOOOOOOO OOOOOOOOOO гчгчгчгчгчгчгчгчгчгч гбоб^^кбоог^г^од qqqqqqqqqq OLnrHoLnrHood^fx-i ONHNHOHONH

OOoiOOHHNNHNNcn q q н н v41 r-1 r-1 н q q q q rsL6r-io)7;d(7)c6'7:N(7)(7) МНОНОМОМНОНО

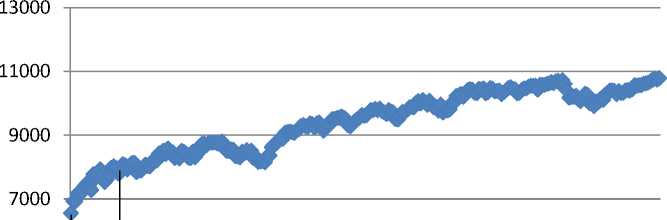
Рис. 3. Диапазоны вложения с минимальным риском по индексу индексу Dow Jones с 09.03.2009 по 22.03.2010

На рисунке 3 представлен диапазон, в котором риск вложения средств в инвестиционный проект минимален.

Далее рассмотрим достаточно продолжительную предысторию индекса Dow Jones с 04.03.2003 по 03.01.2012.

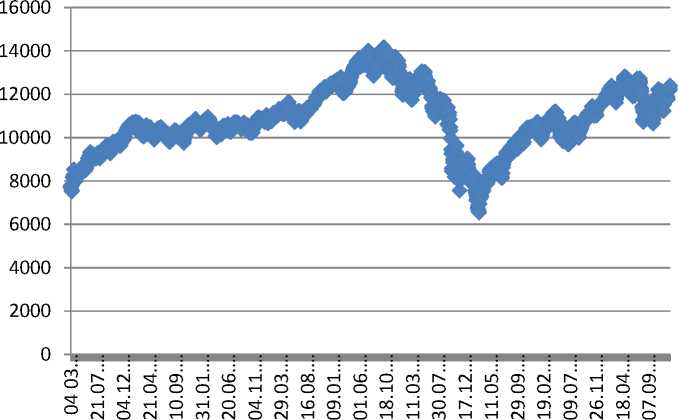
Индекс Dow Jones, данные с 04.03.2003 по 03.01.2012

Рис. 4. Индекс Dow Jones с 04.03.2003 по 03.01.2012

Рассмотрев структуру, можно выделить следующие направления изменения данного показателя (табл. 1).

Структура изменения индекса Dow Jones с 04.03.2003 по 03.01.2012

Таблица 1

Номер периода	Начало периода	Конец периода	Тип тренда	Продолжительность периода, дн.
1	04.03.2003	22.01.2004	Возрастающий	231
2	22.01.2004	24.03.2005	Постоянный	298
3	24.03.2005	01.10.2007	Возрастающий	637
4	01.10.2007	10.03.2008	Убывающий	111
5	10.03.2008	06.05.2008	Возрастающий	41
6	06.05.2008	09.03.2009	Убывающий	212
7	09.03.2009	22.03.2010	Возрастающий	262
8	22.03.2010	02.07.2010	Убывающий	74
9	02.07.2010	03.05.2011	Возрастающий	211
10	03.05.2011	18.08.2011	Убывающий	75
11	18.08.2011	03.01.2012	Возрастающий	95

Как показали расчеты для возрастающих трендов, во всех случаях был оптимальным знакоположи-

“ 9   9   9

+ ■•■. Порядок авторегрессии при этом

тельный нормированный числовой ряд У —г =--+--+ м10 i  10 100

в среднем составил 17, как и в приведенных расчетах. Поэтому порядок определения и полученную величи- ну риска можно сохранить для случаев возрастания.

Следует отметить тот факт, что сохранение вида числового ряда и порядка авторегрессии при моделировании всех участков дает возможность утверждать о постоянстве характерного фактора, изменяющего направление развития уровня деловой активности в США.

Величину продолжительности промежутков на всех периодах возрастающего тренда определим по формуле

n

8 = ¹ ^ ь , n i = 1 k

где д - продолжительность промежутков периода; k - длина периода; n - количество периодов. Определим среднюю продолжительность интервалов возрастающего тренда д = 1У li- = 6 Й17

1 231 + 637 + 41 + 262 + 211 + 95

= 14,5 .

6             17

Для выявления интервала с минимальным риском мы должны определить точку min возрастающего тренда или точку начала роста g о . Последующая точка g 1 будет находиться на расстоянии д = 14,5 дн. от g ₀ . Аналогичным образом выявим и другие точки. По той причине, что только в первый промежуток риск минимален, поэтому весь возрастающий тренд можно разбить на 2 интервала.

Подведем итог полученных расчетов (табл. 2).

Соответствия значений данного ряда уровню риска для возрастающего тренда

Таблица 2

	Возрастающий тренд
Risk	0	0,9
Степень риска	Низкая	Высокая
Продолжительность	[ g 0, g 1)	[ g 1, g 17 ]

Продолжительность выделенных периодов в большинстве случаев не превышает года, поэтому предложенный подход позволяет оценить возможный риск инвестиционного проекта на краткосрочную и среднесрочную перспективу с полным возвращением инвестиций в этот период.

Методика оценки риска целесообразности инвестирования в различные моменты времени на основе МЧР по индексу USDX

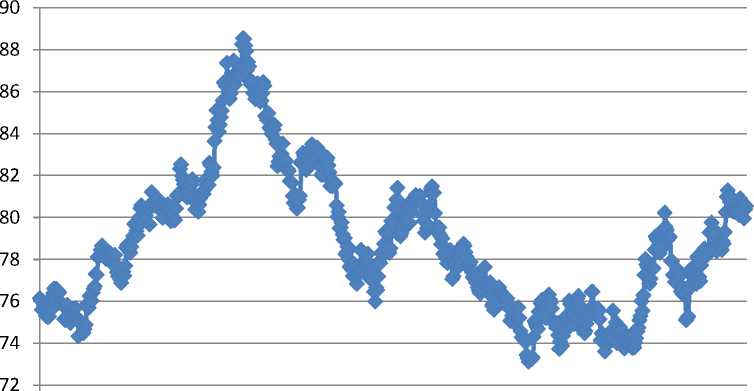
Рассмотрим индекс USDX в период с 10.10.2009 по 05.01.2012 (рис. 5).

ООООООООНннннннннннн оооооооооооооооооооо

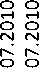
НННРт^ГЧГЧГЧГЧГЧГЧГЧГЧхНхНхНхНхН^

Индекс USDX с 10.10.2009 по 05.01.2012

Рис. 5. Индекс USDX с 10.10.2009 по 05.01.2012

Выделим структуру изменения данного индекса и типы тенденции на разных участках.

Таблица 3

Номер периода	Начало периода	Конец периода	Тип тренда	Продолжительность периода, дн.
1	10.10.2009	25.11.2009	Убывающий	39
2	25.11.2009	06.06.2009	Возрастающий	163
3	06.06.2009	06.08.2010	Убывающий	54
4	06.08.2010	31.08.2010	Возрастающий	22
5	31.08.2010	04.11.2010	Убывающий	57
6	04.11.2010	26.12.2010	Возрастающий	45
7	26.12.2010	29.04.2011	Убывающий	108
8	29.04.2011	23.05.2011	Возрастающий	21
9	23.05.2011	03.06.2011	Убывающий	11
10	03.06.2011	26.08.2011	Постоянный	73
11	26.08.2011	03.10.2011	Возрастающий	33
12	03.10.2011	27.10.2011	Убывающий	22
13	27.10.2011	14.12.2011	Возрастающий	42
14	14.12.2011	05.01.2012	Убывающий	19

Структура изменения индекса USDX с 10.10.2009 по 05.01.2012

Рассмотрим индекс USDX c убывающей динамикой в период с 10.10.2009 по 25.11.2009.

Расчеты показали, что с минимальной ошибкой Д = 0,0276 , или Д = 2,76% , лучшим будет тот же

“ 9    9    9     9

знакоположительный нормированный числовой ряд У —7 =--+--+--+ - . При этом порядок i=110 i   10 100 1000

модели (длина числового ряда, используемая для аппроксимации) равен 4 значениям.

Разобьем исходный ряд данных на 4 примерно равных промежутка по 9–10 значений, так же преобразуем исходный индекс в кусочно-линейную функцию. Первый промежуток будет с 10.10.2009 по 22.10.2009. Для каждого из этих промежутков можно определить величину риска. Так, риск для первого промежутка будет

Riski = Pin = 1 - У— = 1 -Г — + — + -9- + —9—1 = 0,0001 .

• ¹    In i “1 10 i L 10 100 1000 10000 J

  Второй промежуток с 23.10.2009 по 11.03.2009, риск будет

  Risk₂ = P_In = 1-У — = 1 - — +    +     = 0,9001 .

• ²    In     =io i      100 1000 1000

Последний промежуток с 15.11.2009 по 25.11.2009, риск в этот промежуток составит

Risk ₄

= P in = ^{1 -} E— = 1 ^{1 -} i =4 10 i

« 1 .

Дальнейшие расчеты по убывающим трендам показали, что порядок авторегрессии колеблется от 2 до 4 значений, поэтому выберем среднее значение, равное 3.

Так как риск минимален в первом промежутке каждого периода, поэтому, согласно формуле (6), определим продолжительность данного промежутка

1Л li 1 39 + 54 + 57 + 108 + 11 + 22 + 19

= 14,76 .

— 5 -L =---

• ⁷    = 3  7             3

Средняя продолжительность промежутков составляет 14,76дн. при минимальном уровне риска для данного индекса.

Определяем точку min убывающего тренда или точку начала спада g ₀ . Последующая точка g ₁ будет находиться на расстоянии 3 = 14,76 дн. от g о . Аналогичным образом выявим и другие точки ( g 2 ,g 3 ). По той причине, что только в первый промежуток риск минимален, весь убывающий тренд можно разбить на 2 интервала.

Подведем итог полученных расчетов по методике оценки риска целесообразности вложения средств в инвестиционный проект на основе МЧР по индексу USDX (табл. 4).

Соответствия значений данного ряда уровню риска для возрастающего тренда

Таблица 4

	Убывающий тренд
Risk	0,0001	0,9
Степень риска	Низкая	Высокая
Продолжительность	[ g 0, g 1)	[ g 1, g 3]

Предложенные методики позволяют предварительно оценить величину риска целесообразности вложения средств в инвестиционный проект по одному из предложенных факторов. Наилучшим промежутком вложения средств является интервал по продолжительности 2–3 недели с момента начала роста индекса Dow Jones или с момента снижения индекса USDX, поскольку оба этих фактора имеют обратную зависимость по коэффициенту корреляции Спирмена. В дальнейшем предполагается более детальная проработка данной методики в определении других факторов, позволяющих оценить предварительную величину риска на прединвестиционной стадии.

При рассмотрении приведенных выше методик динамика факторов рассматривалась на локальных (возрастающих, убывающих) трендах. В стратегическом анализе локальные колебания индексов могут находиться в стадии рецессии или развития глобального экономического цикла. Далее, в пунктах 4 и 5, будут рассмотрены методики, учитывающие колебания, протекающие в фазе рецессии и роста экономического цикла.

Методика оценки риска целесообразности инвестирования в различные моменты времени на основе МЧР по усредненному тренду фазы рецессии индекса USDX

Объединим выделенные периоды индекса USDX согласно стратегическому анализу по фазам экономического цикла (табл. 5).

Фазы изменения индекса USDX с 10.10.2009 по 05.01.2012

Таблица 5

Фаза	Начало	Конец	Тип тренда	Продолжительность, дн.
1	10.10.2009	06.06.2009	Возрастающий	202
2	06.06.2009	26.08.2011	Убывающий	391
3	26.08.2011	05.01.2012	Возрастающий	116

Как и в предыдущем случае, будем рассматривать убывающий тренд.

Расчеты показали, что с минимальной ошибкой Д = 0,0086 , или Д = 0,86% , лучшим будет знако-

А 8  8  8

положительный нормированный числовой ряд ^ — = ^ + jj + '” • При этом порядок модели равен 4

значениям.

Разобьем исходный ряд данных на 4 примерно равных промежутка по 97–98 значений, так же преобразуем исходный индекс в кусочно-линейную функцию. Выделим промежутки и определим величину риска. Так, риск для первого промежутка будет

Risk i = Pm = 1 — Z — = 1

i = 1 ⁹

—

88  8   8

--1---1---1--

9  81  729  6561

\

= 0,000152 .

Второй промежуток, риск будет

Risk 2 = P = 1 — Z 77 = 1 — i = 2 ⁹

-+--- +

81  729

= 0,889 .

Риск в последний промежуток составит

Risk 4 = P i, = 1 — Z 77 = 1

i = 4 ⁹

—

« 1 .

Подведем итог полученных расчетов по данной методике (табл. 6).

Соответствия значений данного ряда уровню риска для фазы рецессии

Таблица 6

	Убывающий тренд
Risk	0,000152	0,889	1
Степень риска	Низкая	Высокая	Очень высокая
Продолжительность	[ g 0, g 1)	[ g 1 , g 2)	[ g 2, g 4]

Риск будет минимален только на первом промежутке и составит 98 дн., что соответствует 3 месяцам после начальной точки пика. Далее приведем визуализацию полученных расчетов (рис. 6).

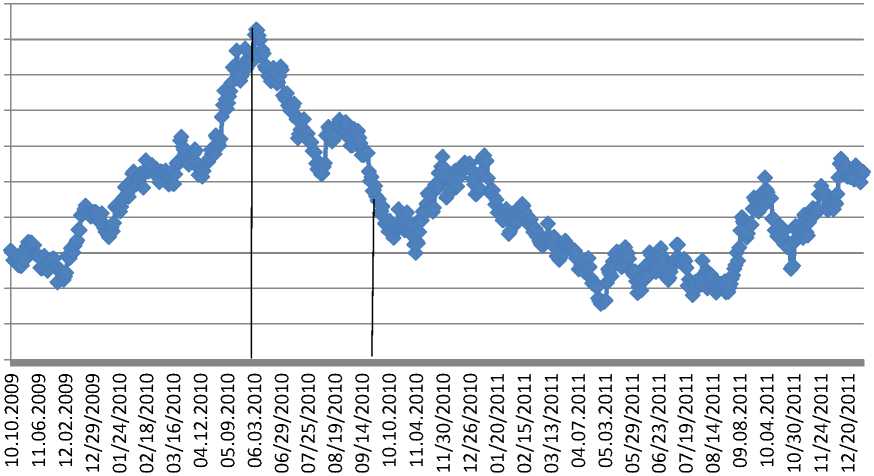
Индекс USDX с 10.10.2009 по 05.01.2012

Рис. 6. Диапазоны вложения с минимальным риском по индексу USDX в динамике с 10.10.2009 по 05.01.2012

На рисунке 6 представлен диапазон вложения средств в инвестиционный проект с минимальной степенью риска с 06.06.2009 по 27.09.2010.

Методика оценки риска целесообразности инвестирования в различные моменты времени на основе МЧР по усредненному тренду фазы развития индекса Dow Jones

Ранее мы разбили индекс Dow Jones на 11 интервалов возрастания и убывания (табл. 1), объединим данные периоды, согласно стратегическому анализу, в 3 фазы (табл. 7).

Фазы изменения индекса Dow Jones с 04.03.2003 по 03.01.2012

Таблица 7

Фаза	Начало	Конец	Тип тренда	Продолжительность, дн.
1	04.03.2003	01.10.2007	Возрастающий	1164
2	01.10.2007	09.03.2009	Убывающий	362
3	09.03.2009	03.01.2012	Возрастающий	714

Рассмотрим первую фазу данного индекса с 04.03.2003 по 01.10.2007, продолжительностью 1164 дн.

Расчеты показали, что с минимальной ошибкой А = 0,00721 , или А = 0,721% , лучшим будет зна-

9    9    9     9

коположительный нормированный числовой ряд У —г =--+--+--+ - . При этом порядок моде- i=110i   10 100 1000

ли равен 12 значениям. Так как ряд остался тот же и близкий порядок модели, полученные оценки параметров модели являются состоятельными, несмещенными и эффективными.

Разобьем исходный ряд данных на 12 примерно равных промежутков по 97 значений, преобразовав исходный индекс в кусочно-линейную функцию. Риск для первого промежутка будет

Risk, = P_In = 1 -У — = 1 - — + — +     + - -9

• 1           ^10 i      L10 100   100010

Риск второго промежутка будет

Riski = p!n = 1 -У — = 1--+----+----й «

• 2          ^10i 100  1000     101210

В последующие промежутки риск растет незначительно. Риск в последний промежуток составит

Risk ,2 = P i. = ¹ - X 777 = 1 - i = 17 ¹⁰

Расчеты 3-й фазы показали, что порядок модели и числовой ряд сохранились. Определим среднюю продолжительность интервалов возрастающего тренда

S =1X -=

2 S'12

1 1164 + 714

2      12

= 78,25 .

Для выявления интервала с минимальным риском мы должны определить точку min возрастающего тренда или точку начала роста g 0 . Последующая точка g 1 будет находиться на расстоянии S = 78,25 дн. от g ₀ . Аналогичным образом выявим и другие точки. По той причине, что только в первый промежуток риск минимален, весь возрастающий тренд можно разбить на 2 интервала.

Подведем итог полученных расчетов (табл. 8).

Соответствия значений данного ряда уровню риска для фазы развития

Таблица 8

	Возрастающий тренд
Risk	0	0,9
Степень риска	Низкая	Высокая
Продолжительность	[ g 0 , § 1 )	[ g 1 , g 17]

Далее приведем визуализацию полученных расчетов (рис. 7), на данном рисунке приведен график индекса Dow Jones в динамике с 04.03.2003 по 03.01.2012 и выделены интервалы вложения средств в инвестиционный проект с минимальной степенью риска. Каждый из выделенных диапазонов по продолжительности равен примерно 78 дн., что соответствует первой волне экономического роста.

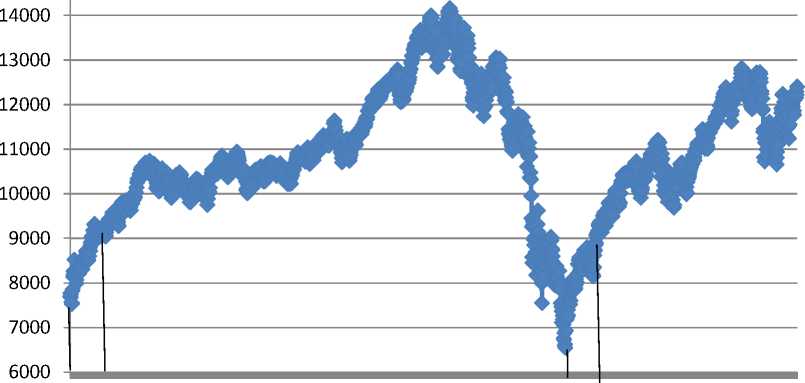
cncnm^^^lr)LЛLЛLr)ЮФ^D^^^ooooooa1Cлa)OOOHr^г^ ООООООООООООООООООООООНННННН оооооооооооооооооооооооооооо гчгчгчгчгчгчгчгчгчгчгчгчгчгчгчгчгчгчгчгчгчгчгчгчгчгчгчгч cnkbONL/icnHLncnN^odN^odHfnr^HfnuiONkDcSHLna) ОО^ОООООО^ОО^ОО^ОО^ОО^ОООООО ^^^^^^.^^Ti^.o^SP^dxi,® ^л5 ci-yi^,-^ co о о о о Индекс Dow Jones, данные с 04.03.2003 по 03.01.2012

Рис. 7. Диапазоны вложения с минимальным риском по индексу Dow Jones в динамике с 04.03.2003 по 03.01.2012

Выводы. Подводя итог, заметим что полученные значения рисков и соответствующие им интервалы говорят о безрисковости вложений средств в инвестиционный проект в период не более 3 месяцев с начала подъема экономики после рецессии, что согласуется с базовой теорией экономического развития.