Об одной контракции дискретной группы D3

Дискретные симметрии играют важную роль в физике. Одним из примеров является CPT-инвариантность — фундаментальная симметрия физических законов. В калибровочных теориях дискретные симметрии возникают в различных аспектах. Многие фундаментальные характеристики полей и элементарных частиц могут описываться не группами Ли, как принято, а дискретными группами симметрий. Например, группу диэдра D 3 с образующими R 1 и R 2 и соотношениями R 2 = 1 и ( R 1 R 2 ) ³ = 1 можно взять в качестве симметрии триплета SU (3) кварков [1].

Неабелевы дискретные симметрии играют заметную роль в моделях смешивания лептонов и могут появиться при спонтанном нарушении симметрии неабелевой непрерывной калибровочной теории [2–7].

Дискретные группы движений пространств постоянной кривизны (пространств Евклида E ⁿ , Лобачевского H ⁿ , сфер S ⁿ ) возникают и в различных областях математики и ее приложений [8]. Например, группы симметрии правильных многогранников и кристаллов и т.д.

On one contractionof a discrete group D3

I.V. Kostyakov, V.V. Kuratov

Institute of Physics and Mathematics,

Federal Research Centre Komi Science Centre, Ural Branch, RAS, Syktyvkar

The groups of motions of two-dimensional space-time models from a geometric point of view are groups of motions of two-dimensional homogeneous spaces of a constant curvature. When quantizing these models, discrete subgroups of these groups play an important role. The standard model is based on the gauge groups U (1), SU (2) and SU (3). Discrete subgroups of these groups are now also in the center of attention in the elementary particle physics. In this paper we present contractions of the discrete dihedron group D 3 induced by limit transitions in the continuous group O (2) and O (3). The resulting groups are D 4 and infinite groups D ∞ , generating discrete lattices of two-dimensional spacetime models. We also discuss transitions of discrete symmetry groups of the Platonic solids.

Дискретные подгруппы группы Лоренца возникают при построении теории квантованного пространства-времени, которое обладало бы некоторой дискретной симметрией, переходящей в лоренцеву симметрию в континуальном пределе. При таком дискретном преобразовании пространство-время, представлямое 1+3-мерной решеткой, должно переходить само в себя [11]. Например, в работе Дирака [12]

изучалась дискретная подгруппа группы Лоренца, которая в сочетании с дискретными подгруппами трансляций давала дискретную подгруппу группы Пуанкаре, и были рассмотрены простейшие четырехмерные пространственно-временные решетки.

Дискретные группы позволяют находить точные решения квантовых систем. Например, принцип инвариантности относительно дискретной подгруппы Лоренца, действующей независимо на состояния частиц с различными импульсами, приводит к определению всех элементов двухчастичной S -матрицы, удовлетворяющей уравнению треугольников (или уравнению Янга-Бакстера) [13].

Группа диэдра D 3 может рассматриваться как дискретная подгруппа непрерывных групп O (2) или O (3) , контракции которых хорошо изучены [14]. Мы приведем несколько примеров, куда перейдет D ₃ при некоторых контракциях непрерывных групп O (2) и O (3) и как при этом выглядят орбиты этих дискретных групп в соответствующих одно- и двумерных пространствах Кэли-Клейна.

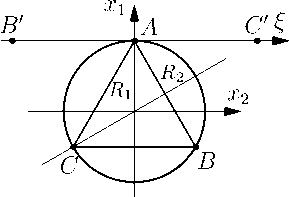
Рисунок 1. Правильный треугольник ( n = 3 ) на окружности S ¹ евклидовой плоскости.

Figure 1. Regular triangle ( n = 3 ) on the circle S ¹ of the Euclidean plane.

Данная группа изоморфна полупрямому произведению Z ₂ и Z _n . Генетический код этой группы можно задавать разными способами, выбирая разные образующие [15]. Например, R I = 1 , R ⁿ = 1 , ( R 1 R ) ² = 1 или R 2 = 1 , R 2 = 1 , ( R 1 R ₂ ) ⁿ = 1 , где R ₂ можно выбрать как отражение относительно прямой, повернутой на угол ^π _n относительно оси x 1

1. Дискретные группы в одномерных пространствах Кэли-Клейна

Одномерные группы вращения Галилея и Минковского можно записать единым образом [14], используя параметр контракции j = 1 , I, i , i ² = 0 , i ² = — 1

R 2 =

cos —

■ ^тг

— sin —

_

_

sin — & cos — п

,

/ cos jt

\ j sin jФ

—j sin jt cos jt

)

Они являются группами симметрии соответствующих окружностей S 1 ( j ) на плоскостях R ₂ ( j ) = ( x 1 ,jx ₂ )

„2 , -2 2       2

X 1 + j X 2 = a

R 2 = 1 , R 1 R 2 = R.

Действуя на начальную точку A преобразованиями, задаваемыми элементами всей группы, можно получить остальные точки правильного n -угольника. На рис. 1 изображен случай треугольника n = 3 .

Для эллиптической геометрии на прямой с бельтрами-евой координатой 5 = a Х 1 отражения R 1 и R ₂ из группы диэдра D ₃ выглядят следующим образом

е = R 1 • ^ = Ч,

и сохраняют метрику ds2 = dxl + j 2 dx2. (3)

Вышеприведенные формулы описывают одномерные пространства и группы Кэли-Клейна. В случае j = 1 , формула (1) дает обычные вращения, при j = i или j = i получим

G = ( 10 ) ил" G = ( ch t t t ) • (4) у ф 1 у у sh ф ch ф J определяющие группу поворотов (сдвигов) на плоскости Галилея и группу лоренцевых вращений на плоскости Минковского. В последних двух случаях x1 интерпретируется как время t, а x2 — как одномерное пространство r.

Опишем дискретные подгруппы этих групп. Рассмотрим группу симметрии правильного n -угольника, или группу диэдра D _n . Ее можно реализовать как дискретную подгруппу O (2) , состоящую из группы вращений с образующей

R = f cos n    sin2n ) , Rn = 1

\ sin — cos / и образующей

R1 = ( 0 —1 ) • R2 = 1 •(6)

являющейся отражением относительно оси x 1 .

‘'

^{е    R 2 5}     1 _— V 3 e •

a а действие образующей R = R 1 R2 циклической подгруппы вращения имеет вид

5 ' = R5 = т^ = —R 2^ . a

Орбита представленной групп ы состоит из точек A, B ^′ , C ^′ с координатами 5 B ‘ = — V3 a , 5 A = 0 , 5 с ‘ = V3 a

(рис. 1). При этом отражение R ₂ оставляет на месте точку C ^′ и меняет местами точки A и B ^′ . Отражение R ₁ оставляет на месте точку A и меняет местами точки B ^′ и C ^′ . Поворот R точку B ^′ переводит в A , точку A переводит в C ^′ и точку C ^′ — в B ^′ .

Теперь посмотрим, куда перейдет группа симметрий правильного n -угольника при j = i в формулах (1), (2). Образующие R 1 и R 2 при этом будут иметь вид

R - - (0 —— 1) • R 2 - ( 1 — °! ) •

R ₁ ² = R ² ₂ = 1 .

Здесь мы обозначили v = — 2П . R 1 — отражение относительно оси x 1 , R 2 — отражение относительно прямой, параллельной оси x 1 , находящейся на расстоянии ^v ₂ от нее.

При непрерывном аналоге j = е ^ 0 контракции j = ι можно считать, что совершается непрерывное устремление радиуса окружности к бесконечности a → ∞ , при котором прямые, пересекающиеся в центре окружности под углом ϕ становятся параллельными. Произведение двух отражений относительно параллельных осей, разделенных расстоянием ^v ₂ , будет сдвигом («вращением» на плоскости Галилея) на v . Матрица сдвига, являющаяся в этом случае и образующей подгруппы сдвигов («вращений») на плоскости Галилея, имеет вид

R = RR = ( ^{1 0} У R n = ( ^{1 0} У (7) \ v 1 У \ nV 1 У

Подгруппа с образующей R изоморфна Z , а вся группа D ∞ , построенная на двух образующих R 1 и R 2 или R 1 и R , изоморфна полупрямому произведению Z 2 и Z . Стартуя с начальной точки A , действуя отражениями R 1 и R 2 , можно получить всю решетку на окружности плоскости Галилея (рис. 2).

x 1

A

R 1     R 2

x 2 ---►

Рисунок 2. Решетка на окружности плоскости Галилея, полученная действием R 1 , R 2 .

• Figure 2.    Lattice on a circle of the Galilean plane, obtained by the action of R i ,R 2 .

Возможен еще один выбор образующих, а именно — R и R ^′ ₁

R1 = ( —1°).              (8>

Тогда, начиная с точки A , действуя R ^′ ₁ и R , получим решетку на всей окружности (рис. 3).

x 1

A x2 ►

Рисунок 3. Решетка на окружности плоскости Галилея, полученная действием R ' 1 , R .

• Figure 3.    Lattice on a circle of the Galilean plane, obtained by the action of R 1 ,R .

Все то же самое можно проделать и на гиперболической прямой ( j = i ). В этом случае

R i =(0 — .) ■ R 2 =(sh v^— ch v ) ■ (9)

R ₁ ² = R ² ₂ = 1 , R ₁ R ₂ = R.

Образующая подгруппы ”вращений”

R = RR = ( ^ch v ^{— sh} v ¹² у — sh v ch v у ,

R ⁿ =

ch nv — sh nv

— sh nv ch nv

.

Здесь мы имеем пример фуксовой группы, т.е. дискретной подгруппы группы движений гиперболической плоскости. Ее действие на окружности в пространстве Минковского изображено на рис. 4, 5.

Таким образом, дискретные подгруппы диэдра D _n группы O (2) при контракциях переходят в подгруппы диэдра D _∞ групп Галилея и Лоренца. Отметим, что группы D _∞ являются и группами симметрии пространственновременных решеток на плоскостях Галилея и Минковского, изображенных на рис. 6 и 7.

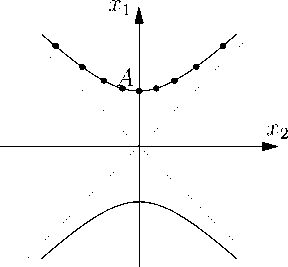
Рисунок 4. Решетка на окружности плоскости Минковского, полученная действием R 1 , R 2 .

Figure 4. Lattice on a circle in the Minkowski plane, obtained by the action of

R i ,R 2 .

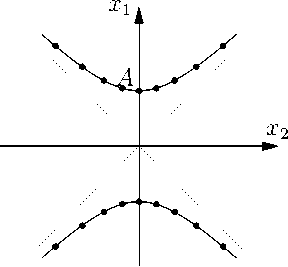
Рисунок 5. Решетка на окружности плоскости Минковского, полученная действием R 1 , R .

Figure 5. Lattice on a circle in the Minkowski plane, obtained by the action of

R' ‘ ,R .

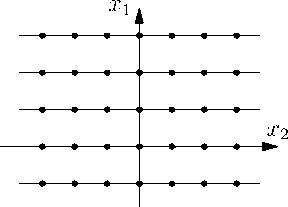
Рисунок 6. Пространственно-временная решетка на плоскости Галилея.

Figure 6. Space-time lattice on the Galilean plane.

x 1

/ cos j 1 ф

R 12 =     j 1 ^{sin j} 1 ^ф

—j 1 sin j 1 ф cos j 1 ф 0

Рассмотрим простой пример группы симметрии пра-

вильного треугольника, расположенного в евклидовом пространстве R ₃ (1 , 1) , как показано на рис. 8. Образующие этой группы, являющиеся отражениями относительно плоскостей x ₁ = x ₂ и x ₂ = x 3 , имеют вид

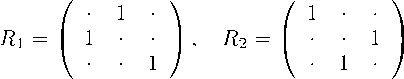
(   ■     ■     1   \

R = R 1 R 2 =    1    ■   ■    .          (12)

у   ■    1    ■  )

x 2

*-

Произведение R = R 1 R ₂ является вращением на угол 120 ° . Определяющие соотношения

Рисунок 7. Пространственно-временная решетка на плоскости Минковского.

• Figure 7. Space-time lattice on the Minkowski plane.

• 2.    Группа диэдра D 3 как дискретная подгруп

Отметим, что все данные формулы можно было бы получить и с помощью комплексных, дуальных и двойных чисел [16]. Единым образом их можно записать в виде z = x 1 + jx2, где j = i, i, e, e2 = 1. Отражения R 1 и R2 в этом случае действуют следующим образом a2                    a2 2π z = R i ■ z = —, z = R 2 ■ z = —e n j, zz а вращения — z = RiR2 ■ z = R ■ z = e2Пjz.

па группы O (3)

Правильные многоугольники и правильные многогранники могут быть вписаны в сферу, вследствие чего их группы симметрии будут дискретными подгруппами группы вращений O (3) .

Двумерные пространства Кэли-Клейна можно реализовать [14] как сферы S ₂ ( j )

x I ⁺ j ² x 2 ⁺ j 11 j 2 x 3 = a ² , j k = 1 ^,| k ,i     ⁽¹⁰⁾

в пространствах R 3 ( j 1 ,j 2 ) = ( x 1 ,j 1 x 1 ,j 1 j 2 x 2 ) с метрикой ds ² = dx 1 + j ² dx 2 + j ² j 2 dx 3 . Здесь i k = 0 , i k i p = i p i k = 0 , k = p, k,p = 1 , 2 . Вращения относительно осей x ₁ , x ₂ и x ₃ описываются матрицами

( 10    0

R 23 =   0 cos j 2 ф -j 2 sin j 2 ф ,

• \    0 j2 sin j 2 ф    cos j 2 фУ

• (    cos j 1 j 2 ф    0 -j 1 j 2 sin j 1 j 2 ф \

R13 =          0        1         0

• \    A sin j 1j2 ф 0    cos j 1j2 ф/

• 3.    Группа симметрий правильного треугольни

R 2 = 1 , R 2 = 1 ,   R ³ = 1 .          (13)

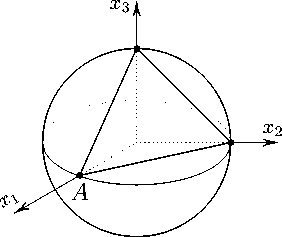
Рисунок 8. Положение правильного треугольника в евклидовом пространстве R ₃ (1 , 1) .

Figure 8. Position of a regular triangle in the Euclidean space R ₃ (1 , 1) .

ка в пространствах Кэли-Клейна R ₃( j 1 , j 2 )

В расслоенном пространстве R ₃ ( 1 1 , 1) с одномерной базой {x 1 } и двумерным евклидовым слоем {x 2 , x 3 } , используя формулы (11), (12), находим вид образующих дискретной группы

• ( 1    ■     ■  \              ( 1   ■    ■\

R1 = v — 1 ■    , R 2 =     ■ ■ 1

• у  ■     ■     1 у               у  ■    1    ■)

( 1   ■     ■\

R = R1R2 =    v  ■  -1    .(14)

■1

Определяющие соотношения

R 2 = 1, R 2 = 1, R4 = 1

задают группу симметрии квадрата (рис. 9). Начиная, например, с точки A , действуя всеми элементами этой группы, получим еще три точки, расположенные на плоскости x 1 = a , являющиеся вершинами правильного квадрата.

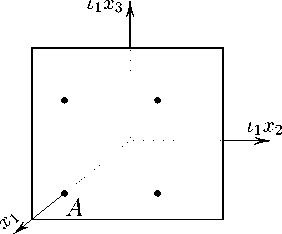
Рисунок 9. Квадрат в расслоенном пространстве R 3 ( i 1 , 1) с одномерной базой {х 1 } и двумерным слоем {х 2 , х 3 } , полученный действием R 1 ,R 2 .

Figure 9. Square in the fibered space R 3 ( i 1 , 1) with one-dimensional base {x 1 } and two-dimensional fiber {x 2 ,x 3 } , obtained by the action of R 1 ,R 2 .

Оператор “вращения”

R = R 1 R 2 = I v

■

■■

B1        ■ w — 1

порождает бесконечную подгруппу с элементами

R ^{2 n}

1 ■

■■

nvw

1            ■

B 2 nw  1

,

R ² n+1 =

v

Bnvw

■■

B 1

.

2 nw 1

Действительно, матрицы R ₁ и R ₂ в рассмотренном случае определяют отражения относительно прямых x 2 = av и x 2 = x 3 в двумерном слое {x 2 ,x 3 } в точке базы x 1 = a . Эти прямые пересекаются под углом 45 ° , поэтому композиция двух отражений R 1 и R 2 даст поворот на 90 ° .

Действуя на точку A элементами указанной группы, задаваемой образующими R ₁ , R ₂ и соотношениями (16), получим решетку на окружности плоскости Галилея x 1 = a (рис. 10).

где

R = v

■

■

■

■

1   = TGT - ¹

■

v

2 v

■■

1 ■

■ 1

1 ■

■

■

■

■

B 1

■

■■

v

2   1

v

2        1

,

v

T 2

v

■■

1 ■

■ 1

,

есть операция сдвига в пространстве R 3 ( i 1 , 1) . При этом все операторы преобразуются как TGT - ¹ .Таким образом, имеем в слое x ₁ = a вращение на 90 ^° с центром, смещенным в точку ( a, av/ 2 , av/ 2) .

Отметим, что если бы мы выбрали другое расположение правильного треугольника в пространстве R 3 (1 , 1) , то получили бы иной результат, так как при этом в слое {x ₂ , x 3 } в точке базы x 1 = a прямые, относительно которых происходят отражения, были бы расположены под другим углом. Если этот угол равен ^π _n , то получим группу диэдра D n , для других значений углов получим группу симметрии D ^ .

В дважды расслоенном пространстве R 3 ( i 1 ,i ₂ ) , в котором слой {x ₂ , x 3 } в свою очередь расслоен с базой {x ₂ } и слоем {x 3 } , образующие R 1 , R ₂ из (12) принимают вид

R 1 = v

■■

B

■■

1 ■

, R 2 =

■

■

■■

w

.

Определяющие соотношения

R ₁ ² = 1 , R ₂ ² = 1 .

B 1

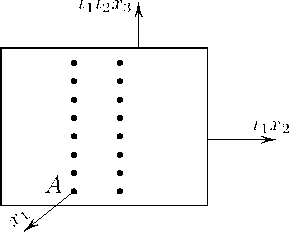
Рисунок 10. Решетка в дважды расслоенном пространстве R 3 ( i 1 , i 2 ) , полученная действием R 1 , R 2 .

Figure 10. Lattice in a doubly fibered space R 3 ( i 1 , i 2 ) , obtained by the action R 1 , R 2 .

В однократно расслоенном пространстве R 3 (1 ,i 2 ) с двумерной евклидовой базой {x 1 , x 2 } и одномерным слоем {x 3 } образующие R 1 , R 2 из (12) принимают вид

R i =

■

■

■■

■■

, R 2 =

■

■

■

v

■

■

— 1

.

Определяющие соотношения

R 1² = 1 , R 2²

Оператор “вращения”

= 1 .

■

R = R i R 2 =   1

■

■

■

■

v — 1

порождает бесконечную подгруппу с элементами

R ² n+1 =

■

Bnv

■

( n + 1) v

■

■

— 1

,

_R 2 n

1 ■

nv

■■

1 ■

Bnv 1

.

Действуя на точку A элементами всей группы, задаваемой образующими R 1 , R 2 и соотношениями (18), получим решетку на цилиндре x 2 + x 2 = a ² (рис. 11).

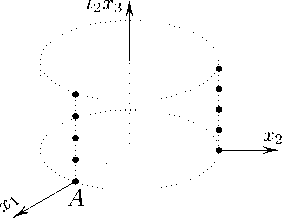
Рисунок 11. Решетка в однократно расслоенном пространстве R 3 (1 , 1 2 ) с двумерной евклидовой базой {x 1 , x 2 } и одномерным слоем {x 3 } , полученная действием R 1 , R 2 .

Figure 11. Lattice in a singly fibered space R 3 (1 , i 2 ) with two-dimensional Euclidean base {x 1 , x 2 } and one-dimensional fiber {x 3 } , obtained by the action R 1 , R 2 .

• 4.    Группы симметрии правильных многогранников

Группу симметрии правильного n-угольника можно задать с помощью отражений относительно двух плоскостей, угол между которыми равен ^π _n . Схема Кокстера-Дынкина [8, 15] для этого случая представлена на рис. 12.

n

Рисунок 12. Диаграмма Кокстера-Дынкина для правильного n -угольника. Figure 12. Coxeter-Dynkin diagram for a regular n -gon.

Данные плоскости можно представить уравнениями

52 a ij X j =0 ,     i =1 , 2 ,          (21)

j =1

где a 1 j и a 2j , j = 1 , 2 , 3 задают два вектора, перпендикулярные этим плоскостям.

Правильные многогранники — тетраэдр, октаэдр, куб, додекаэдр и икосаэдр, можно вписать в сферу, и их группы симметрии являются дискретными подгруппами группы O (3) [8,15], элементы которых порождаются отражениями относительно трех плоскостей

52 a ij X j = 0 ,     i = 1 , 2 , 3 ,          (22)

j =1

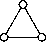
углы между которыми равны ( ^п , ^п , п ) в случае тетраэдра, ( П , п , п ) для куба и октаэдра и ( п , п , п ) для икосаэдра и додекаэдра. Соответствующие диаграммы Кокстера-Дынкина представлены на рис. 13(a), 13(b) и 13(c).

О--О--О О--0=0 о-- о--о abc

Рисунок 13. Диаграммы Кокстера-Дынкина для правильных многогранников.

Figure 13. Coxeter-Dynkin diagram for regular polyhedrons.

• 5.    Пространство R ₃( i 1 , 1)

В пространстве R ₃ ( 1 1 , 1) сфера радиуса а переходит в слой x 1 = а . Тогда, полагая в уравнениях (21) для двух плоскостей x 1 = а , получаем дискретную группу, порожденную отражениями относительно двух прямых

• 52 aij Xj + aai 1 = 0, i = 1, 2.(23)

j =2

Предполагая a i2 = 0 , можно переписать уравнения прямых (23) в виде

X2 = ki(X3 - dз) + d2, i =1,2,(24)

здесь ( d 2 ,d ₃ ) — точка пересечения этих прямых, k i = tg ф _i = — a i 2 . Тогда отражения R 1 и R 2 относительно указанных прямых задаются формулами

Ri = TOiT -1,(25)

где операция сдвига

/  1    •    •\

T =   d 2  1

d3   •1

и отражения

/ 1        •               •\

O i =     • cos 2 ф _i   sin 2 ф _i      , O i = 1 .

\ •   sin 2 ф i — cos 2 фi /

Вращение, задаваемое композицией отражений R 1 и R 2 , имеет вид

R = R i R 2 = TO i O 2 T - ¹ .         (26)

Если угол ϕ 1 - ϕ 2 между этими прямыми равен _m ^π , то R m = 1 , и мы имеем конечную группу диэдра D m . Таким образом, при контракции группа диэдра D n может перейти при некоторых положениях правильного n-угольника, вписанного в сферу, в D m .

Три плоскости (22), определяющие группы симметрий правильных многогранников, в слое X 1 = a задают дискретную группу, порожденную отражениями относительно трех прямых

52 aijXj + aai 1 = 0, i = 1,2, 3.(27)

j =2

Предполагая a i2 = 0 , можно переписать уравнения прямых (27) в виде

X 2 = kiX з + di,      i = 1,2, 3,(28)

здесь ( d _i , 0) — точки пересечения этих прямых оси X ₂ , k i = tg ф _i = — a i ^.Тогда три базовых отражения R i относительно этих прямых задаются формулами

Ri = TOiT-1, i = 1, 2, 3,(29)

где оператор сдвига теперь равен

/ 1     ••

Ti =    di 1 •,

\ •     •1 / а оператор отражения имеет прежний вид

/ 1        •               •\

Oi =    • cos 2 фi    sin 2 фi

\ •   sin 2 ф _i — cos 2 ф _i 1

Каждая пара прямых определяет дискретную подгруппу поворотов, задаваемую композициями R 1 R 2 , R 2 R 3 и R 1 R 3 . Чтобы эти подгруппы были конечными, разности углов между данными прямыми А ф 12 = \ф 1 — ф 2 | , А ф 23 = |ф 2 — ф 3 | и А ф 31 = |ф 3 — ф 1 | должны быть равны п , п , _k ^π ₃ соответственно, где k i ∈ N . Имеем треугольник, образованный тремя прямыми с углами _k ^π _i . Так как сумма углов в треугольнике равна π , получаем уравнение на числа k _i

^44=! ■ k1    k2    k3

Оно имеет только три решения [8] в виде троек (3 , 3 , 3) , (2 , 4 , 4) и (2 , 3 , 6) . Таким образом, если углы между этими прямыми равны ⁽ п , П , П ) , ⁽ п , п , П ) или ⁽ П , П , П ) , то имеем дискретную группу, порождающую решетку на евклидовой плоскости в слое. Диаграммы Кокстера-Дынкина для этих групп представлены на рис. 14.

a

0=0=0 b

о--а

c

Рисунок 14. Диаграммы Кокстера-Дынкина для дискретных групп в пространстве R ₃ ( i 1 , 1) .

Figure 14. Coxeter-Dynkin diagrams for discrete groups in space R ₃ ( i 1 , 1) .

• 6.    Пространство R3(l 1,i2)

Если обе прямые (23) не лежат в слое x2 = b, то уравнения (23) можно записать в виде x3 = Vix2 + di, i =1,2.(31)

Тогда отражения R ₁ и R ₂ относительно этих прямых задаются формулами

Ri = TiPiT-1,  Ri = 1,(32)

где

/ 1     • • \              / 1     ••

Ti =  I •    1    •   I , Pi = I •     1

di   •   1                   •   2vi

Вращение, задаваемое композицией отражений R ₁ и R ₂ , имеет вид

R = R1R 2 = TKT -1,  Rn = TK nT -1,(33)

где

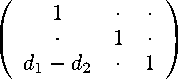
/  1              •              •

K =     •       1        •

\  •   2( v 1 — v 2 )   1

и определяет бесконечную циклическую группу, изоморфную Z . Таким образом, в каждом слое x 2 = b будет своя решетка со своим шагом, представляющая орбиту группы диэдра D ∞ .

Если же одна из прямых, задающих отражение, совпадает со слоем x 2 = b , то у нас появляется еще отражение между слоями. Пример такой решетки изображен на рис. 10.

На плоскости Галилея есть прямые двух типов [17]. Первый тип — прямые вида x 3 = vx 2 + d , второй тип — прямые вида x 2 = b . Если обозначить светлым кружком зеркало в виде прямой первого типа, а темным кружком — зеркало, как прямую второго типа, то на плоскости Галилея можно определить три типа диаграмм Кокстера-Дынкина (рис. 15).

∞∞  ∞ ab  c

Рисунок 15. Диаграммы Кокстера-Дынкина для дискретных групп на плоскости Галилея.

Figure 15. Coxeter-Dynkin diagrams for discrete groups on the Galilean plane.

Первый и третий типы диаграмм определяют дискретные группы, орбитами которых являются решетки в слое и в базе соответственно. В случае симметрий платоновых тел, если пересечения трех плоскостей (22) со слоем x 1 = a имеют вид прямых первого типа (31), то три отражения R i дискретной группы будут иметь вид (32). Каждая пара отражений задает решетку в слое со своим шагом.

Заключение

Контракции непрерывных групп Ли, описанные в [14] с помощью коммутативных нильпотентных образующих ι k , допускают адекватное описание посредством непрерывных вещественных параметров ε k , которые стремятся к своим нулевым предельным значениям е _к ^ 0 . Предельный переход в непрерывной группе влечет за собой переходы в соответствующих дискретных подгруппах и, соответственно, изменение орбит этих групп.

Отметим, что в случае контракций компактных групп Ли обычно получаются некомпактные группы. В наших примерах конечные дискретные группы переходят в бесконечные дискретные группы. В случае, когда при контракции исходной непрерывной группы имеется инвариантная компактная подгруппа, то соответствующая ей дискретная подгруппа остается конечной. Этот пример возникает при контракции в пространстве R ₃ ( 1 1 , 1) .