Об одной математической модели электропотребления с учетом данных мониторинга
Автор: Пронина Е.А.
Журнал: Вестник Красноярского государственного аграрного университета @vestnik-kgau
Рубрика: Трибуна молодых ученых
Статья в выпуске: 9, 2013 года.
Бесплатный доступ
В статье рассматриваются уровни и режимы бытового электропотребления в Красноярском крае. Проводится анализ регрессии и определяется оптимальная модель для описания потребления электроэнергии.
Электропотребление, регрессия, корреляция, мониторинг, модель, красноярский край
Короткий адрес: https://sciup.org/14083278
IDR: 14083278 | УДК: 519.6
Текст научной статьи Об одной математической модели электропотребления с учетом данных мониторинга
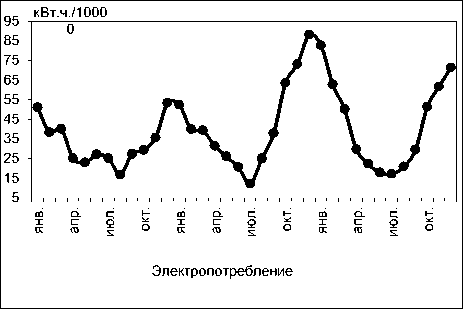
На производство и потребление электроэнергии оказывают влияние множество факторов. При построении модели в качестве объясняющих переменных рассмотрены номер наблюдения, длина светового дня, температура (для сопоставимости их масштабов нормируем электропотребление в 0,0001 раза), приведенные на рис 1.
Для анализа были использованы среднемесячные показатели за 3 года, приведенные в табл. 1 [1, 2].
Бытовое потребление электроэнергии, длина светового дня, температура
Таблица 1
|
Номер наблюдения (N) |
Месяц |
кВт.ч/10000 (Е быт. ) |
Длина дня, ч (L) |
Температура, 0С (t) |
|
1 |
2 |
3 |
4 |
5 |
|
1 |
Январь |
510123 |
7,030 |
-20,7 |
|
2 |
Февраль |
382345 |
9,083 |
-10,2 |
|
3 |
Март |
400023 |
11,400 |
-3,5 |
|
4 |
Апрель |
251288 |
14,012 |
4,0 |
|
5 |
Май |
229338 |
16,356 |
10,2 |
|
6 |
Июнь |
270146 |
17,983 |
18,1 |
|
7 |
Июль |
251154 |
17,639 |
17,6 |
|
8 |
Август |
166987 |
15,706 |
16,6 |
|
9 |
Сентябрь |
273114 |
13,217 |
10,3 |
|
10 |
Октябрь |
292400 |
10,728 |
-1,0 |
|
11 |
Ноябрь |
355809 |
8,267 |
-14,3 |
|
12 |
Декабрь |
532584 |
6,683 |
-17,0 |
Окончание табл. 1
|
1 |
2 |
3 |
4 |
5 |
|
13 |
Январь |
523887 |
7,030 |
-23,4 |
|
14 |
Февраль |
399125 |
9,083 |
-13,7 |
|
15 |
Март |
392113 |
11,400 |
-5,3 |
|
16 |
Апрель |
313420 |
14,012 |
6,2 |
|
17 |
Май |
260102 |
16,356 |
15,1 |
|
18 |
Июнь |
205578 |
17,983 |
22,0 |
|
19 |
Июль |
121214 |
17,639 |
21,5 |
|
20 |
Август |
249374 |
15,706 |
23,2 |
|
21 |
Сентябрь |
378690 |
13,217 |
14,3 |
|
22 |
Октябрь |
634957 |
10,728 |
9,2 |
|
23 |
Ноябрь |
729843 |
8,267 |
-5 |
|
24 |
Декабрь |
880214 |
6,683 |
-12,4 |
|
25 |
Январь |
826095 |
7,030 |
-6,4 |
|
26 |
Февраль |
627282 |
9,083 |
-4,1 |
|
27 |
Март |
500250 |
11,400 |
1,4 |
|
28 |
Апрель |
296211 |
14,012 |
7,1 |
|
29 |
Май |
222954 |
16,356 |
18,4 |
|
30 |
Июнь |
178092 |
17,983 |
18,6 |
|
31 |
Июль |
171468 |
17,639 |
22,8 |
|
32 |
Август |
208548 |
15,706 |
17,8 |
|
33 |
Сентябрь |
293791 |
13,217 |
11,2 |
|
34 |
Октябрь |
511710 |
10,728 |
2,63 |
|
35 |
Ноябрь |
615869 |
8,267 |
-4,9 |
|
36 |
Декабрь |
712594 |
6,683 |
-14,04 |
-5
-10
-15
-20
-25
19 часы
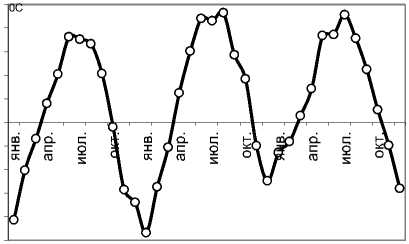
Температура

Длина дня
Рис. 1. Электропотребление, длина дня, температура
График потребления электроэнергии показывает, что оно происходит с некоторой периодичностью, связанной со сменой времени года, т.е. сезонностью. Для определения ее периода построим и исследуем периодограмму (рис. 2), значения которой вычисляются как
Pk = N ■ (Ak2 + Bk2 ), (k = 1-W (N = 36), где Аk – коэффициент при косинусе, а Вk – коэффициент при синусе на частоте k в разложении Фурье; N – количество наблюдений. Значения периодограммы можно интерпретировать как дисперсию (вариацию) данных на соответствующей частоте [3].
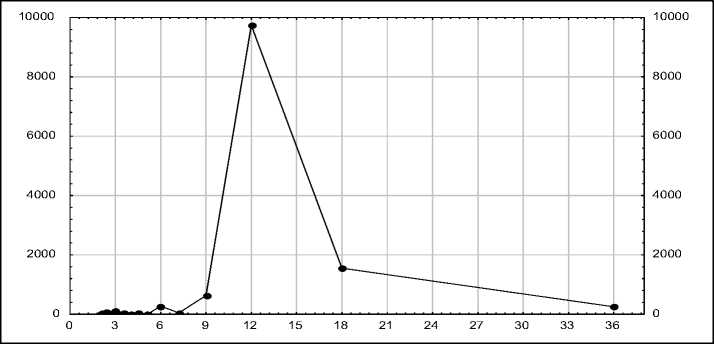
Рис. 2. Периодограмма
На ней присутствует отчетливый пик с периодом, равным двенадцати. Для определения тенденции потребления электроэнергии построим парную регрессию, зависящую от N по методу наименьших квадратов (рис. 3) [4, с. 62–64]:
Е = 30,6384 + 0,4713 ■ N , ( N = 1...36 ).
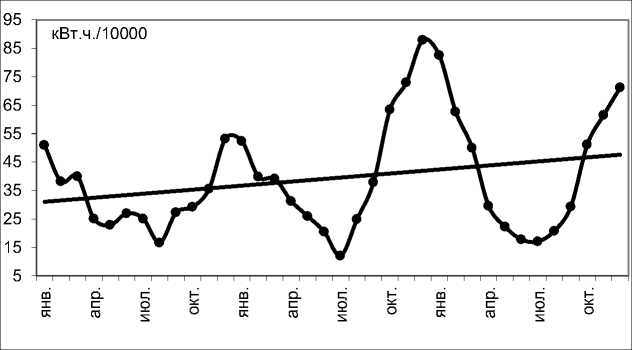
Рис. 3. Линейная регрессия
По наклону линии регрессии и по коэффициенту при N можно сказать, что потребление электроэнергии за рассматриваемый период имеет незначительную тенденцию к увеличению.
Произведем вычисление описательных статистик для потребления электроэнергии, приведенные в табл. 2.
Таблица 2
|
Среднее Е ср. |
39,3575 |
|
Нижняя граница для среднего (-95 %) |
32,6632 |
|
Верхняя граница для среднего (+95 %) |
46,0517 |
|
Стандартное отклонение среднего ( o < ) |
19,7849 |
|
Стандартная ошибка среднего (SE) |
3,2975 |
|
Минимум (E min ) |
12,1214 |
|
Максимум (E max ) |
88,0214 |
|
Медиана |
33,4615 |
|
Асимметрия |
0,8607 |
|
Эксцесс |
-0,1035 |
Описательные статистики
Значение асимметрии показывает, что распределение сильно отличается от нормального (сдвинуто вправо). Это можно объяснить тем, что объем электропотребления растет из года в год. При этом график потребления электроэнергии не имеет резко выраженного пика (показатель эксцесса близок к нулю).
По графикам продолжительности светового дня и температуры видно, что между потреблением и температурой, а также длиной дня, присутствует отрицательная корреляция, т.е. при увеличении температуры или длины дня потребление снижается. Рассчитаем корреляции между этими величинами. Результаты приведены в табл. 3.
Корреляционная таблица
Таблица 3
|
Показатель |
Потребление |
Номер наблюдения |
Длина дня |
Температура |
|
Потребление |
1 |
0,2510 |
-0,8478 |
-0,6999 |
|
Номер наблюдения |
– |
1 |
-0,0228 |
0,1795 |
|
Длина дня |
– |
– |
1 |
0,9349 |
|
Температура |
– |
– |
– |
1 |
Наиболее значимые корреляции наблюдаются между потреблением и длиной дня, температурой и потреблением, а также между температурой и длиной дня. Поэтому целесообразно включить в модель переменные – длину дня (L) и температуру (t). В то же время достаточно высокая корреляция между потреблением электроэнергии и температурой (около 70 %) возникает оттого, что температура и длина светового дня очень тесно коррелированны (R = 93,5 %), поэтому включение в модель одновременно этих переменных может привести к получению ненадежных оценок регрессии (мультиколлинеарности) [4, с. 155]. Также температура является случайной величиной, поэтому лучше включить в модель только длину светового дня (неслучайную величину).
В общем виде линейная регрессия примет вид (рис. 4, табл. 4):
-
• Регрессия 1: E = b + a 1 L + u , (1)
где b – свободный член; a 1 – параметр; u – случайная составляющая.
Оценка параметров регрессии 1
Таблица 4
|
Параметр |
b |
a 1 |
|
91,8001 |
-4,2491 |
|
|
Стандартная ошибка |
5,8979 |
0,4557 |
|
t-статистика (df=34) |
15,5650 |
-9,3235 |
|
p-уровень |
0,0000 |
0,0000 |
|
Коэффициент корреляции (R) |
84,78 % |
|
|
Коэффициент детерминации (R2) |
71,88 % |
|
|
Скорректированный коэффициент детерминации (R a 2) |
71,06 % |
|
|
Сумма квадратов отклонений (SS) |
3851,98 |
|
По полученным результатам построим график:
E = 91,8001 - 4,2491 • L
.
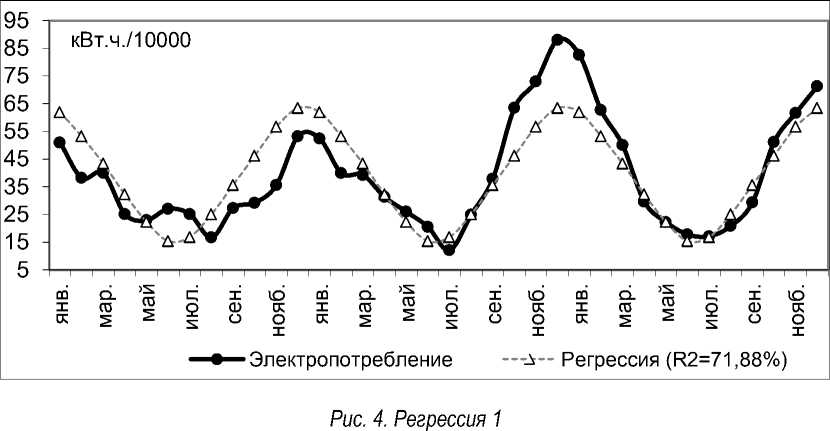
Сформулируем нулевую гипотезу о том, что коэффициенты регрессии равны нулю, а затем попытаемся опровергнуть ее (для принятия гипотезы должно выполнятся неравенство: -t крит. < t < t крит. ). По значениям t-статистики можно сказать, что величины оценок свободного члена b и коэффициента a отличаются в действительности от нуля, так как их t-статистики не попадают в интервал [-t крит. < t < t крит. ] (критическое значение для t при 5-процентном уровне значимости с 34 степенями свободы равняется 2,032), что также следует из уровня значимости р (р < 0,05) [4, с. 97].
Хотя зависимость электропотребления от номера наблюдения невелика (25,10 %), для улучшения регрессии включим его в модель, тогда получим (рис. 5, табл. 5):
• Регрессия 2: E = b + a 1 L + a2 N
Оценка параметров регрессии 2
Таблица 5
|
Показатель |
b |
a 1 |
a 2 |
|
Параметры |
83,4217 |
-4,2226 |
0,4352 |
|
Стандартная ошибка |
6,1652 |
0,4162 |
0,1560 |
|
t-статистика (df=33) |
13,5310 |
-10,1456 |
2,7907 |
|
p-уровень |
0,0000 |
0,0000 |
0,0087 |
|
R |
87,89 % |
||
|
R 2 |
77,25 % |
||
|
Ra 2 |
76,58 % |
||
|
SS |
3113,50 |
||
Значения t-статистики и р-уровня показывают, что оценки параметров регрессии значимы на уровне 0,05. Коэффициент R2 увеличился примерно на 5,37 %, что связано с добавлением в уравнение дополнительной переменной N.
E = 83,4217 - 4,2226 • L + 0,4352 • N .
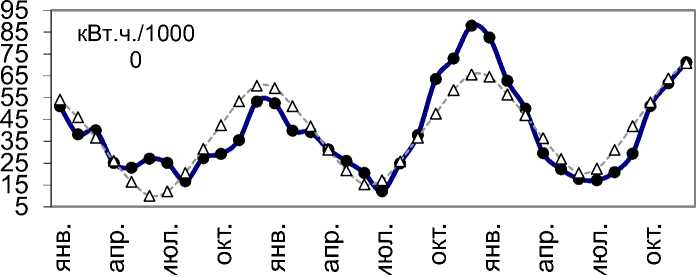
Электропотребление Регрессия (R2=77,25%)
Рис. 5. Регрессия 2
Уравнение регрессии можно интерпретировать следующим образом. При увеличении какой-либо независимой переменной на единицу, электропотребление увеличится (уменьшится) на величину коэффициента этой переменной. Например, при увеличении длины дня (L) на 1 ч и неизменном номере месяца (N) электропотребление изменится на -4,2226 (кВт.ч/10000).
При визуальном анализе графика электропотребления заметно его сходство с периодической функцией. Поэтому добавим в уравнение какую-либо из функций, например, такого вида: cos ( a - X + а ) или sin ( a - X + а ) , которую определим экспериментально (для регрессии (2) наилучшей является функция sin ( a - N ) ) (рис. 6, табл. 6). Тогда получим уравнение:
-
• Регрессия 3: E = b + а 1 L + а 2 N + а 3 sin ( а 4 N ) . (3)
Е = 77,8461 - 4,2076 - L + 0,7273 - N - 10,6711 - sin ( 12,223 - N )
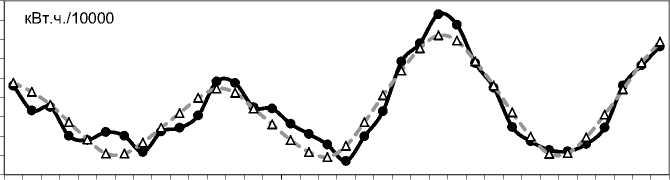
Электропотребление
Регрессия 3 (R2=90,04%)
Оценка параметров регрессии 3
Таблица 6
|
Показатель |
b |
a 1 |
a 2 |
a 3 |
a 4 |
|
Параметр |
77,8461 |
-4,2076 |
0,7273 |
-10,6711 |
12,2230 |
|
Стандартная ошибка |
4,3325 |
0,2855 |
0,1170 |
1,7669 |
0,0078 |
|
t-статистика (df=31) |
17,9679 |
-14,7396 |
6,2154 |
-6,0394 |
1574,0656 |
|
p-уровень |
0,0000 |
0,0000 |
0,0000 |
0,0000 |
0,0000 |
|
R |
94,89 % |
||||
|
R2 |
90,04 % |
||||
|
Ra 2 |
89,75 % |
||||
|
SS |
1364,15 |
||||
Рис. 6. Регрессия 3
Одновременно с этим электропотребление носит нелинейный характер, поэтому преобразуем независимые переменные, возведя их в некоторую степень n . (рис 7, табл. 7). Модифицированное уравнение будет выглядеть следующим образом:
Регрессия 4: E = b + a 1 Ln 1 + a 2 Nn 2 + a 3 sin l a 4 Nn 3
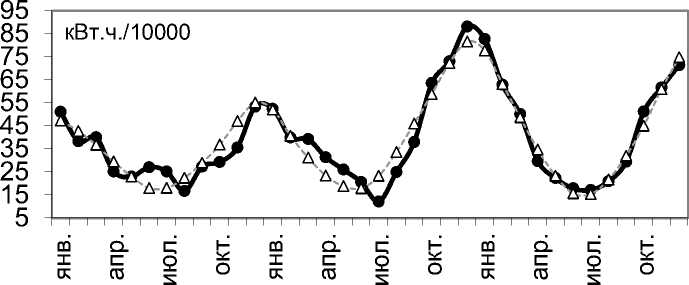
Электропотребление Регрессия (R2=92,29%)
Оценка параметров регрессии 4
Таблица 7
|
Показатель |
b |
a 1 |
a 2 |
a 3 |
a 4 |
|
Параметр |
222,0121 |
-131,7167 |
24,9494 |
10,9948 |
0,3448 |
|
Стандартная ошибка |
14,3706 |
7,5532 |
3,4317 |
1,5016 |
0,0060 |
|
t-статистика (df=31) |
15,4491 |
-17,4385 |
7,2703 |
7,3218 |
57,8154 |
|
p-уровень |
0,0000 |
0,0000 |
0,0000 |
0,0000 |
0,0000 |
|
n1 |
0,22300 |
||||
|
n2 |
0,22306 |
||||
|
n3 |
1 |
||||
|
R |
96,07 % |
||||
|
R 2 |
92,29 % |
||||
|
R a 2 |
92,07 % |
||||
|
SS |
1056,01 |
||||
E = 222,0121 - 131,7167 • L’22 2 + 24,9494 • ^ °’22306 +10,9948 • sin ( 0,3448 • N )
Рис. 7. Регрессия 4
В результате включения в регрессию (2) функции синуса и преобразования переменных коэффициент R2 вырос на 15,04 % (R a 2 – на 15,49 %). Оценки параметров регрессии значимы на уровне 0,05, и мы получили достаточно высокое значение коэффициента детерминации.
Теперь проверим, превышает ли R2 то значение, которое может быть получено случайно. Для этого проверим, является ли значимой совместная объясняющая способность k (k =2) независимых переменных при помощи F-теста (т.е. выполняется ли условие F > F крит. ):
F =
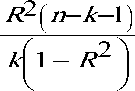
= 197,57; .
Критический уровень F с 2 и 33 степенями свободы при уровне значимости в 1 % составляет 5,31. Таким образом, F-статистика, равная 197,57, указывает на значимый уровень объяснения [4, с. 160].
Для того чтобы модель была адекватна описываемым данным, должны выполняться четыре условия Гаусса-Маркова [4, с. 80–81]:
-
- математическое ожидание остатков равно нулю;
-
- дисперсия остатков в каждом наблюдении постоянна (гомоскедастична);
-
- отсутствие автокорреляции остатков;
-
- остатки должны быть распределены независимо от объясняющих переменных.
Так как большой проблемой при моделировании временных рядов является проблема автокорреляции остатков, то первым проведем тест на ее наличие.
В регрессии (1) количество объясняющих переменных равно единице (k = 1) и статистика Дарбина-Уотсона (d крит. ) равна 0,47 при верхней границе (D U ), равной 1,32, и нижней границе (D L ), равной 1,21, при уровне значимости в 1 %. Значит, можно сделать вывод о том, что остатки положительно коррелированны (d крит. < D L ) и модель будет неадекватной. То же можно сказать и о регрессии (2), в которой имеется две объясняющих переменных, d крит. = 0,58, а D U = 1,38 и D L = 1,15 (d крит. < D L ).
Модели (3) и (4) содержат две объясняющих переменных. Для третьей модели d крит. = 1,16, для четвертой – d крит. = 1,29 находятся между нижней и верхней границами (1,15 < d крит. < 1,38). То есть мы не можем ни подтвердить, ни отклонить гипотезу о наличии автокорреляции.
Это можно заметить по графикам автокорреляционных функций остатков (рис. 8) [4, с. 221].
Regress 1
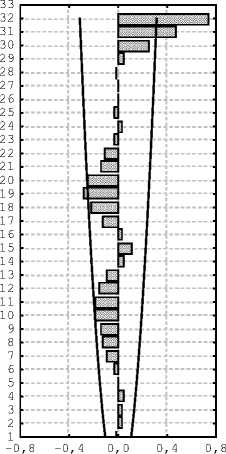
Regress 2
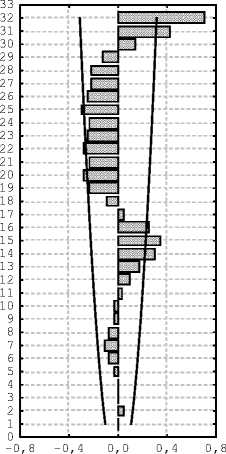
Regress 3
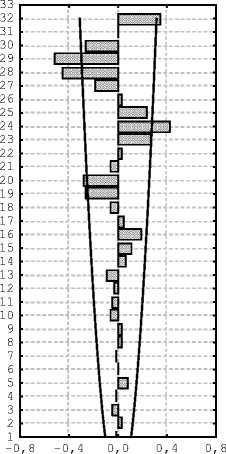
Рис. 8. Автокорреляционные функции остатков регрессии (1),(2),(3) и доверительные интервалы
Так как регрессия (4) более точно соответствует наблюдаемым данным, то проверку выполнения остальных трех условий Гаусса-Маркова сделаем только для нее.
-
• Первое условие о том, что математическое ожидание остатков равно нулю, выполняется автоматически, так как если в уравнение регрессии включен постоянный член, то он ''компенсирует'' систематические смещения остатков.
-
• Гипотезу о том, что дисперсия остатков в каждом наблюдении постоянна, проверим с помощью теста Голдфелда-Квандта. После его проведения мы не отклоняем ее при однопроцентном уровне значимости [4, с. 207–208].
-
• Четвертое условие Гаусса-Маркова о том, что остатки должны быть распределены независимо от объясняющих переменных (или более сильное предположение, что объясняющие переменные не являются
стохастическими) также выполняется автоматически, так как в модель включены переменные, не имеющие случайную составляющую.
Наряду с условиями Гаусса-Маркова обычно предполагается нормальность распределения остатков. Проверим это с помощью исследования показателей асимметрии (S), эксцесса (K) и их стандартных ошибок ( σ S , σ K ), (табл. 8).
Показатели асимметрии, эксцесса и их стандартные ошибки
Таблица 8
|
Показатель |
Значение |
Стандартная ошибка |
|
Асимметрия |
-0,3027 |
0,3925 |
|
Эксцесс |
-0,5667 |
0,7681 |
При нормальном распределении показатели асимметрии и эксцесса равны нулю и по расчетам видно, что по абсолютной величине они имеют тот же порядок, что и их ошибки. Следовательно, ни одна из полученных величин не значима и гипотеза о нормальном характере распределения принимается [3, с. 134]. Это также видно по стандартному нормальному вероятностному графику (рис. 9).
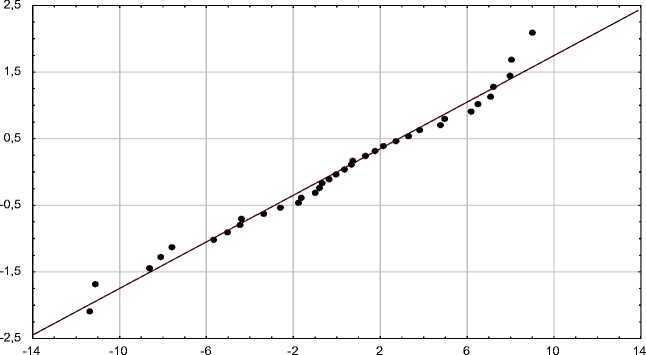
Рис. 9. Стандартный нормальный вероятностный график остатков регрессии 3
Заключение. Модель (4) достаточно адекватна, и ее можно использовать для описания потребления электроэнергии.


