Об одной модели кавитационного течения электролита при электрохимической обработке

Одной из актуальных задач теории электрохимической обработки (ЭХО) металлов [2; 3; 4; 13] является разработка методов расчета формы поверхностей, образующихся в процессе ЭХО, с учетом гидродинамики течения электролита в промежутке между неизвестной границей обрабатываемой детали (анода) и заданной границей электрода-инструмента (катода).

В работе [11] на основе модели идеального процесса [3] решена двумерная задача, связанная с определением установившейся или стационарной [8; 9] границы анода с учетом кавитационного течения электролита в межэлектродном промежутке. Для описания течения использована модель идеальной несжимаемой жидкости [1]. В модели задачи рабочая часть катода представлена полубесконечной пластиной, совершающей поступательное движение к обрабатываемой заготовке с постоянной скоростью V_c , причем направление подачи перпендикулярно указанной границе катода.

В данной работе приводится решение задачи при условии, что обработка осуществляется катодом-пластиной, толщина которой пренебрежимо мала, а направление подачи параллельно граням катода.

Выпуск 3/2020

Схема электрохимической обработки

Схема сечения межэлектродного промежутка изображена на рисунке 1- a .

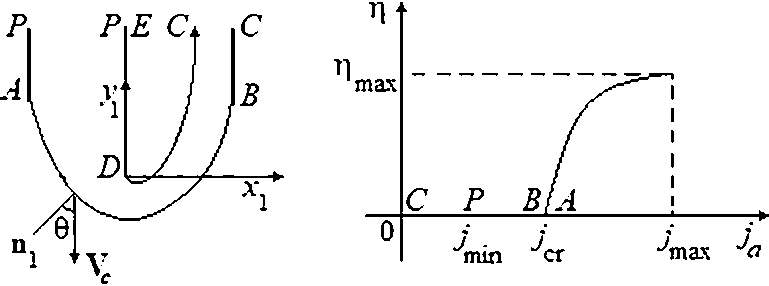
a                                               b

Рис. 1. Межэлектродный промежуток:

a – геометрия межэлектродного промежутка; b – график зависимости η( j_a )

Граница катода-инструмента - пластина PDE. Система декартовых координат ( x₁ , у₁ ) связана с катодом, и ее начало выбрано в точке D . Точки P и E являются бесконечно удаленными. Вектор V _c указывает направление подачи катода. В процессе обработки происходит заглубление катода в тело заготовки, и с течением времени формируется установившаяся анодная граница PABC . Поток электролита направлен от точки P к точке C . В точке D происходит отрыв потока от поверхности катода с образованием каверны, заполненной парами жидкости и газом. Каверна ограничена гранью DE катода и линией DC , простирающейся до бесконечности. Требуется определить установившуюся форму анодной границы PABC .

Для решения задачи необходимо рассмотреть два векторных поля, а именно стационарное электрическое поле и поле скоростей установившегося течения идеальной несжимаемой жидкости в межэлектродном промежутке, а также их взаимосвязь.

Модель электрического поля в межэлектродном промежутке

Для решения задачи используются методы теории функций комплексной переменной [10]. На основе допущений, принятых в работе [3], введем аналитическую функцию W 1 ( z₁) = v ( x₁, y 1 ) + iu ( x₁, y ₁) комплексной переменной z 1 = x₁ + iy₁ , называемой комплексным потенциалом электрического поля. Будем считать, что v ( x₁ , y 1 ) = Re W ( z 1 ) соответствует силовой функции электрического поля, а u(x₁, y ₁) = Im W ( z 1 ) совпадает с потенциалом электрического поля в межэлектродном промежутке. Потенциал u ( x₁ , у₁ ) принимает постоянные значения на границах электродов:

u l pABC = u a , ^U\pd = u c . ⁽¹⁾

В модели каверна считается диэлектриком [11], и ее граница DC является линией уровня функции v(x1, y 1) = Re W (x1, y1). Будем считать, что v(xi, У1)| DC = °. (2)

Для обеспечения точности обработки процесс электрохимического растворения металла локализуется в рабочей зоне, соответствующей нормальной проекции рабочей поверхности катода на обрабатываемую поверхность. За пределами этой зоны скорость растворе-

Миназетдинов Н.М. Об одной модели кавитационного течения электролита...   43

ния металла резко уменьшается вплоть до нуля, при этом на анодной границе формируются участки, на которых растворение металла прекращается. Локализация растворения зависит от многих факторов, в том числе от состава электролита и свойств обрабатываемого материала. Одной из важнейших характеристик локализующих свойств электролита и металла является выход по току η для реакций анодного растворения металла [2].

Для электрохимической обработки сталей с использованием электролитов на основе водных растворов нитрата или хлората натрия введена зависимость выхода по току η от анодной плотности тока j_a [7]:

П(ja ) = 0 пРи 0 < ja ^ kr; П(ja ) = a0 + ai/ja пРи kr < ja ^ jmax, гДе a о > 0, ai < 0, jr - постоянные, Птах = П( jmax ) (РИс 1-b )•

На участке AB анодной границы, соответствующей рабочей зоне, выполняются условия jcr < ja ^ j max, 0 <П^Птах, а нормальная производная потенциала электрического поля удовлетворяет условию [Там же]

d u d n 1

1 (     P Vc   a

----I -ai +--cos 6 К a 0 V £

где κ – удельная электропроводность среды; ε - электрохимический эквивалент металла; ρ - плотность материала анода; θ - угол между вектором V _c скорости подачи катода и вектором n ₁ нормали к анодной границе (рис. 1- а ).

Увеличение межэлектродных зазоров в процессе обработки приводит к уменьшению значений анодной плотности тока, причем на некоторых участках анодной границы плотность тока достигает значений меньше критического j_cr , соответственно, выход по току на этих участках равен нулю. На участке AP плотность тока убывает от значения j_cr в точке A до величины j _min в точке P (см. рис. 1- b ) .

Наличие каверны является дополнительным фактором, способствующим падению анодной плотности тока, а зачастую и возникновению коротких замыканий. Экранирование части анодной границы каверной приводит к тому, что на участке BC плотность тока убывает от значения jcr в точке B до нуля в точке C (см. рис. 1-b). Следовательно, d u _ . d u

= 0.

^К -x          ^j min, -x

О n i P           О n i

Электроизолирующее свойство каверны является причиной отсутствия симметрии межэлектродного промежутка относительно катода-пластины. Положения точек A и B неизвестны и определяются в процессе решения.

Произведем замену переменных по формулам

Y=( u - uc)/(ua - uc), z = z 1/H = x + iy, где ψ – безразмерный потенциал электрического поля; H – характерная длина. Условие (3) можно записать в виде a0к(ua- uc) dy    a

--=---+ cos 6, j 0 H    d ni j 0

где j ₀ =p V _c /£ характерная плотность тока [6].

44 в ыпуск 3/2020

Параметр a 0 является безразмерным, выражение к ( u a — u_c )/ j 0 имеет размерность длины [6], поэтому характерную длину можно задать выражением H = а ₀ к ( u a — u_c )/ j 0 .

Искомые безразмерные геометрические величины должны быть таковы, чтобы безразмерный комплексный потенциал W ( z ) = ф ( x,y ) + i w ( x,у ) , где ф ( x,у ) - гармонически сопряженная функция по отношению к функции w ( x,у ) , согласно формулам (1)-(3)

удовлетворял граничным условиям

^W I pABC 1 , ^W | p _D 0 ; ф| dc = 0 ;

Из формул (4) следует

dW    dw                 а.

--- = — = b + cos 9 , b =—^L.

^d z AB ^d n AB                   j 0

dW  _ 7 jmin

-X a 0   .    , a n p j о

dw

a n c

= 0.

Из условий (5) и первого равенства из условий (8) следует, что безразмерная величина зазора hp на бесконечности в сечении PP hp = -j .                            (9)

j min a 0

Соотношения (5)–(9) будут использованы на следующем этапе, связанном с рассмотре- нием кавитационного течения в межэлектродном промежутке.

Численно-аналитический метод решения

В односвязной области z = x + iy рассмотрим установившееся течение идеальной несжимаемой жидкости, ограниченное прямолинейной стенкой PD , свободной поверхностью DC и твердой границей, состоящей из трех частей – прямой AP , кривой AB , переходящей в прямую BC .

Скорость течения на входе в межэлектродный канал в окрестности бесконечно удаленной точки P равна V_p , а величина скорости на свободной границе DC постоянна и равна V ₀ [1]. Требуется определить формы границ AB и DC .

Для решения задачи введем вспомогательную комплексную переменную t = ξ + i δ, изменяющуюся в области G t ( о <^<л/ 2,0 <5<л|т| /2 ) ( т = i |т| ) (рис. 2), и будем искать функцию z ( t ), конформно отображающую прямоугольник G_t на область течения с соответствием точек, указанных на рисунках 1- а , 2.

Введем в рассмотрение аналитическую функцию W g ( t ) = ф g (t ) + i W g ( t ) - комплекс -ный потенциал течения, где φ _g – потенциал скорости; ψ _g – функция тока и функции Жуковского [Там же]

X(t) = lnV?d7 = r + i9g, r = lnV0, (10) dWg V где V – модуль скорости; θg – угол скорости с осью абсцисс.

Миназетдинов Н.М. Об одной модели кавитационного течения электролита...

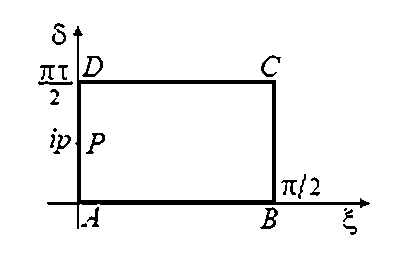
Рис. 2. Плоскость параметрической переменной t

Параметрическую зависимость z ( t ) можно получить с помощью соотношения [1] dz e ^{x (} t * dW g ( t )

dt   V ₀     dt

.

Твердые и свободные границы течения являются линиями тока, на которых Im W g ( t ) = const [Там же], следовательно,

vg (i§) = 0, 8g[0,p); уg (У = 0, ^e[o, п/2]; уg (п/2 + i^) = 0, 5e[o,п|т|/2];

уg(i5) = Q, 5e(p,п|т|/2]; vg(§ + пт/2) = Q, §e[o,п/2], где Q – расход жидкости в струе.

В плоскости комплексного потенциала W_g области течения соответствует полоса ширины Q (рис. 3).

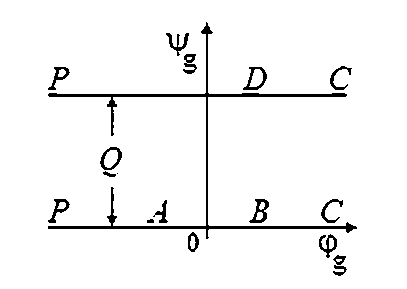
Рис. 3. Область изменения комплексного потенциала Wg ( t )

Функция dW_g dt на горизонтальных сторонах прямоугольника G_t принимает действительные значения, а на вертикальных – мнимые; имеет нули первого порядка в точках A ( t = О ) B ( t = П 2 ) , D ( t = пт/ 2 ) и полюса первого порядка в точках P ( t = ip ) , C ( t = п/ 2 + пт/ 2 ) . Согласно принципу симметрии Шварца [10], функцию dWg/dt можно аналитически продолжить через границы области G_t на всю плоскость. Продолженная таким образом функция будет двоякопериодической с периодами π, πτ и известными особенностями в прямоугольнике периодов [14]. Используя представление эллиптической функции с периодами π и πτ через тета-функции [Там же], найдем

dWL = N    «1 (t)»2 (t)» 4 (t)

dt       «1 (t — ip )«1 (t + ip )«3 (t), где ϑi(t), t = 1, 2, 3, 4 – тета-функции для периодов π и πτ.

46 в ыпуск 3/2020

Интегрированием выражения (12) по дуге полуокружности бесконечно малого радиуса с центром в точке t = ip с помощью теории вычетов [7] найдем n=2Q»3 (ip).

Исследуем область изменения функции Жуковского. Из формулы (10) следует, что вдоль свободной поверхности DC постоянна действительная, а вдоль прямолинейных участков AP , DP , BC – мнимая часть функции χ( t ).

Представим функцию χ( t ) в виде суммы [6]

X ( t ) = X o ( t ) ⁺« ( t ) ,                                ⁽¹³⁾

где X _o ( t ) = r₀ + i ^ _o - функция Жуковского для вспомогательного течения жидкости по заданной схеме при условии, что на границе AB модуль скорости постояне н и равен V _*; w( t ) - функция, аналитическая в области G t и непрерывная в ее замыкании G t = G t ud G , где ∂ G – граница области G_t .

Согласно схеме течения должны выполняться следующие граничные условия:

Im х ( i 6 ) = Im X o ( ^{/ 5} ) = —П 2, 6 e [ o,л|т| /2 ] ;

Im х ( П 2 + i 6 ) = Im X _o ( я/ 2 + / 3 ) = л/ 2, 6e[ o, л|т| /2 J ;          (14)

Re х ( ^ + ПТ/ 2 ) = Re X o ( ^ + пт/ 2 ) = o, ^ e [ o, л/ 2 ^J .

Re X o ( 5 ) = ln VT = r * , ^^{e| o,} П ² ] .                    (15)

*

В плоскости изменения переменной X _o = r o + $_o области вспомогательного течения соответствует прямоугольник G _Xq ( o <  r _o <  r * , — л/2 <0 _o <  л/2 ) (рис. 4).

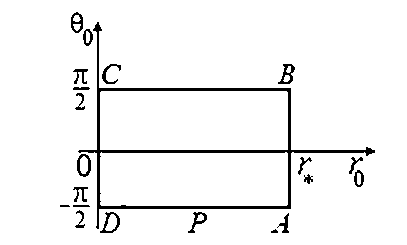
Рис. 4. Область изменения переменной χ₀

Конформное отображение области G t (см. рис. 2) на область G x задается формулой

( л '

² t ^—- ,                         ⁽¹⁶⁾

из которой следует, что г * = Л |т .

Введем для функции χ(t) на криволинейном участке AB граничное условие, являющееся следствием условий (5)–(8) электрохимического формообразования. Рассмотрим соотношение dWg = dWg dW = dWg dt dW dz dW dz dt dW dz .

Миназетдинов Н.М. Об одной модели кавитационного течения электролита...   47

Граница AB является линией тока идеальной жидкости и эквипотенциальной линией электрического поля. На этом участке анодной границы выполняется равенство 0 g ( x , y ) = 0 ( x , y ) . Тогда из условия (7) и формулы (17) следует, что

V =

dW g dz

= ( b + cos 0 g(^)

d ф g d^ d^ d ф

~ п §e 0,2 .

Таким образом, на границе AB граничные значения гармонически сопряженных функций r (ξ) и θ _g (ξ) связаны соотношением

— r

e

( b + Cos 0g ) dфg d^

V ₀      d ^ d ф

Выражение производной d ф _gJd ^ найдем из формулы (12). Для определения производной d ф/ d ^ найдем производную dW[dt комплексного потенциала электрического поля. Согласно соотношениям (5), (6) для функции W ( t ) выполняются следующие граничные условия:

v(i5) = 1, 8е[0,p); ф(^) = 1, ^е[о,п/2]; ф(п/2 + i5) = 1, 5е[о,п|т|/2];

ф(/5) = 0, 5е(p,п|т|/2]; ф(^ + пт/2) = 0, ^е[0,п/2].

Область изменения комплексного потенциала электрического поля представлена на рисунке 5.

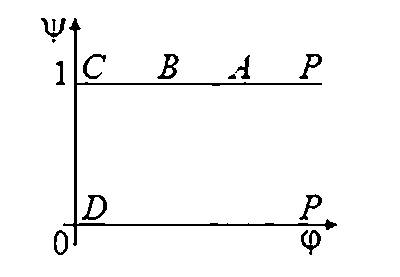
Рис. 5. Область изменения комплексного потенциала W ( t )

Функция dW dt на стороне AB прямоугольника Gt принимает действительные значения, а на сторонах AD, BC и DC - мнимые; имеет нули первого порядка в точках A (t = 0), B (t = П2) и полюс первого порядка в точке P (t = ip). Используя метод особых точек Чаплыгина [1], получим dW = M   «г (t)»2 (t)

dt       « 1 ( t — ip ) « 1 ( t + ip ) ,

M = -~« 3 ( ip ) « 4 ( ip ) .

Используя формулы (12), (19) условие (18) представим в виде

V- ^ ШЬ+C” ’-B>e " = '■         01, откуда при ξ = 0

Q _ ₌1 « 4 ⁽ ip ) « 3 ( 0 ) r ( 0 )

• V , = b « 3 ( ip ) « 4 ( 0 )       .                            ⁽ )

48 в ыпуск 3/2020

Соотношение (20) с учетом равенства (21) представим в виде

¹ ^ 3 ^{( 0} ) ^ ⁴ ( ! ) (b + cos^(^) )e r ^(9— r ⁽⁰⁾ = 1. b ti 4 ( 0 ) ti 3 ( ! ) (           g ^(S))

Учитывая, что Q = V ₀ h_C , где h_C – безразмерная величина зазора на бесконечности в сечении CC , из формулы (21) следует

1 ^ti 4 ⁽ ip ) ^ti з ^{(0) h}C = b ^ 3 ( ip ) ti 4 ( 0 ) ^e

— r (⁰)

.

Из формул (13)–(16) и (22) следует, что для неизвестной функции ω( t ) выполняются следующие граничные условия:

Imw(i5) = 0, Imto(n/2 + i5) = 0, 8е|^0,л|т|/2^|, Re ГО(!+Л1;/2) = 0, £е[0,л/21, b ^( b + sin(2S + ^

В силу условий (22), (25) функцию ω( t ) можно разложить в ряд с вещественными коэффициентами [5; 13]:

о u (t) = 2^ cksh( 01 + 2ti)k, Т1 =л|т.

k = 1

Используя формулы (13), (16) и (27), получим

X(t)=л|т|+iI 2t

— ^Л + 2^ c_fc sh ( т+ 2 ti ) k .

2 7   tr    x

V ^л.

Отсюда из условия % ( ip ) = ln--- i следует, что

V p 2

о

V

—= exp л|т| — 2 p + 2 ^ c k sh ( т 1 — 2 p ) k .

^VP       V               k = 1                   -

Используя равенство V p h p = V ₀ h _C и формулы (23), (29) найдем

L _L V 0_ 1 ^ 4 ( ip ) ^ 3 ( 0 )

hM = h-—=--7—г—^v p     Vp b ^3 (ip)^4 (0)

^

exp — 2 p + 2 ^ c _k ( sh ( T 1 — 2 p ) k — sh T 1 k ) .

^v            k = 1

Из формулы! (27) при условии t = ! , ^е |^0, л/2 J получим

о

Re %(^) = пИ + 2Х Cksh (т1 k )cos(2! k);

k = 1

Миназетдинов Н.М. Об одной модели кавитационного течения электролита...   49

Im x(5) = 2§ + 2^ ckch (T1 k ) sin ( 25 k )—я/ 2, k=1

и условие (26) можно представить в виде

1 63 (0) 64 (5) b 64 (0) 63 (5)

^

b + sin 2 5 + 2 ^ C k ch ( т 1 k ) sin ( 2 5 k )

k = 1

^

= 1

exP 2 ^ c k ^sh ( ^T 1 ^k ) ( 1 — cos

При заданных значениях геометрической величины h_p , коэффициента a ₁ и характерной плотности тока j ₀ =p V_c /£ коэффициенты разложений (27) и математические параметры p , |т| определяются таким образом, чтобы на искомой анодной границе удовлетворялось условие (30) и соотношение (31). Геометрические характеристики определяются из соотношения (11).

Результаты расчетов

Расчеты выполнены для значения a ₁ = –12,818, соответствующего электрохимической обработке сталей в 15%-м водном растворе нитрата натрия [7]. При характерной плотности тока j ₀ = 5 A/см² выполнен расчет координат точек участка AB анодной границы и каверны DC при трех различных значениях величины h_p : 0,2; 0,25; 0,3. В результате выполненных расчетов для заданных величин было установлено, что для указанных значений h_p форма границы DC каверны практически не меняется (рис. 6).

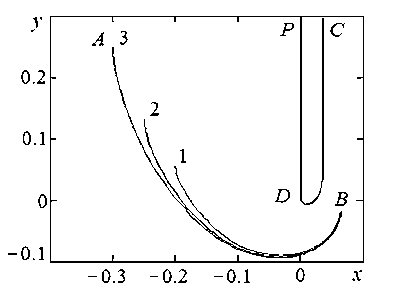
Рис. 6. Результаты расчета границ анода и каверны:

1 – h_p = 0,2; 2 – h_p = 0,25; 3 – h_p = 0,3

В таблице представлены результаты расчета параметров τ, p , ординаты y_A точки A , координаты x_B , y_B точки B , отношения V_p V ₀ и зазора h_C .

Результаты расчета параметров

h p	τ	p	y A	x B	y B	V p / V 0	h C
0,20	0,5142	0,1288	0,0555	0,0630	–0,0163	0,1345	0,0269
0,25	0,5141	0,0801	0,1315	0,0640	–0,0165	0,1097	0,0274
0,30	0,5222	0,0445	0,2493	0,0640	–0,0181	0,0917	0,0275

50 в ыпуск 3/2020

Из таблицы и графиков участка AB анодной границы (см. рис. 6) видно, что координаты точки B и величина h_C практически не зависят от величины h_p .

Аналогичная ситуация имеет место в задаче [12], связанной с определением установившейся анодной границы, при обработке детали трехгранным электродом-инструментом с вертикальными боковыми гранями, одна из которых является диэлектриком.