Об одной модификации вероятностного генетического алгоритма для решения сложных задач условной оптимизации

Необходимость в разработке моделей сложных систем возникает в различных областях науки и техники: математике, экономике, медицине, управлении космическими аппаратами и др. При разработке моделей часто возникают задачи оптимизации, которые обладают такими свойствами, как многоэкстремальность, многокритериальность, алгоритмическое задание функций, сложная конфигурация допустимой области, наличие нескольких типов переменных и т. д. Такие задачи не решаются с помощью классических процедур оптимизации, что приводит к необходимости разраба- тывать и применять более эффективные и универсальные методы. К таким методам относятся, в частности, эволюционные алгоритмы (ЭА), доказавшие свою эффективность при решении многих сложных задач [1; 2].

Эффективность ЭА определяется тщательной настройкой и контролем их параметров. При произвольном выборе параметров неподготовленным пользователем эффективность алгоритма может быть как очень низкой, так и очень высокой, а его надежность изменяться от нуля до ста процентов для одной и той же задачи. В последние годы наблюдается тенденция развития эволюционных подходов, способных к самонастройке параметров за счет использования сложных гибридных схем, а также эффективных алгоритмов с меньшим числом параметров.

Одним из подходов, позволяющих уменьшить число настраиваемых параметров эволюционных алгоритмов, является применение вероятностных генетических алгоритмов, или ВГА [3; 4]. Их отличие от стандартного генетического алгоритма (ГА), в частности, состоит в том, что в них отсутствует оператор скрещивания, а новые решения получаются на основе статистической информации о поисковом пространстве. Таким образом, накапливая и используя эту информацию, данные алгоритмы самостоятельно могут адаптироваться к решаемой задаче.

ВГА показали свою эффективность и применимость к некоторым сложным задачам оптимизации [5; 6] и являются перспективными для дальнейшего изучения и совершенствования. Проблема исследования их специфических свойств на широком классе задач оптимизации, уменьшение количества настраиваемых параметров без потери эффективности является актуальной. Данная работа посвящена исследованию эффективности ВГА в сложных задачах условной оптимизации.

Вероятностный генетический алгоритм безусловной оптимизации. В процессе своей работы ГА накапливают и обрабатывают некоторую ста-тистическую информацию о пространстве поиска, однако эта статистика в явном виде отсутствует. В ВГА предложен следующий способ представления накопленной ГА статистики: на текущей итерации в соответствие популяции решений ставить вектор вероятностей

P k = ( p k , ..., p^k „ ), p^k = P ( X k = 1), i = 1 n , где p _i ^k – вероятность присвоения i -й компоненте вектора решения X^k значения 1; k – номер итерации.

В общем виде работу алгоритма ВГА можно представить следующим образом.

• 1.    Инициализировать случайным образом популяцию решений.

• 2.    С помощью оператора селекции выбрать r наиболее пригодных индивидов текущей популяции (родителей). Вычислить вектор вероятностей по формуле

• 3.    В соответствии с распределением P сформировать популяцию потомков.

• 4.    Применить оператор мутации к популяции потомков.

• 5.    Из популяции родителей и потомков сформировать новую популяцию.

• 6.    Повторять шаги 2–5, пока не выполнится условие остановки.

P = ( P 1 , к, P n ) ,

1 ^r

Pj = P { xj = 1}= S xj, j = 1 n,

Г i = 1

где n – длина хромосомы; xⁱ_j – j -й бит i- го ин дивида.

Как отмечалось ранее, в процессе решения задачи алгоритм накапливает статистику о распределении нулей и единиц в популяции. В ходе проведения численных экспериментов было заме ч ено, что зачастую компоненты вектора вероятностей P сходятся к соответствующим значениям генов оптимального решения (ри с . 1). Выбранная j -я компонента вектора вероятностей P стремится к 1, поэтому, скорее всего, в бинарном представлении оптимального решения ген, стоящий на j -м месте, принимает значение равное 1. Это свойство можно использовать для прогнозирования оптимального решения.

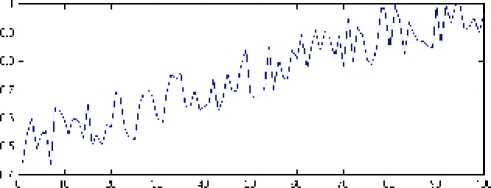
Рис. 1. Значения j -й компоненты вектора вероятностей в зависимости от номера поколения

В [3; 4] был предложен следующий алгоритм прогноза:

• 1.    Для данной задачи выбрать определенную схему ВГА, определить число итераций i = 1, ..., I и число независимых запусков алгоритма к = 1, ..., K .

• 2.    Набрать статистику ( p j ) ^k , j = 1, ..., n . Усреднить ( p_j ) _i по k . Выявить тенденцию изменения компонент p_j .

• 3.    Считать x ‘0 pt = 1, если S( ( P j ) i - 0,5 ) >  0, иначе i = 1

I

• x j op = 0 .

Основная идея данного алгоритма состоит в том, что чем чаще вероятность оказывается больше 0,5, тем вероятнее всего ген в оптимальном решении принимает значение, равное 1.

На практике возможна ситуация, когда в начале работы ВГА накоплено недостаточно информации о поисковом пространстве и значение j -го гена у большинства решений равно 0 (или 1). На более позднем поколении ВГА находит очень хорошее решение, у которого значение j -го гена отличное от ранее встречавшихся, и значения j -й компоненты вектора вероятностей начинают сходиться к противоположному значению (рис. 2). Однако приведенный выше алгоритм прогноза вычислит значение гена, равное первоначальному, поскольку j -я компонента вектора вероятностей продолжительное время оставалась меньше 0,5 (или больше 0,5, если первоначально было значение 1).

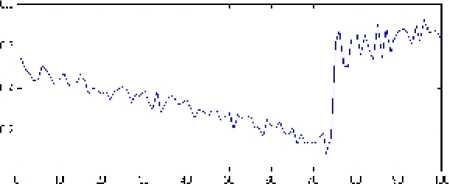
Рис. 2. Ситуация, когда прогноз может быть неверным

Таким образом, можно использовать следующую модификацию алгоритма прогноза.

• 1.    Определить шаг прогноза K .

• 2 .    Через каж дые K поколений по набранной статистике P i , i = 1, N K , N K = t ■ K , t e { 1^2, к } рассчитать изменение вектора вероятностей: A P i = P i - P i - 1 .

• 3.    Каждому поколению придавать вес в зависимости от его номера: о i = 2 i,N_K ( N_K + 1 ) , i = 1, к , ⁿ k .

• 4.    Рассчитать взвешенное изменение вектора вероят-

• NK

• 5.    Рассчитать прогнозируемое оптимальное решение: X op = ( x °^pt ) , где x °^pt = 1, если A~ j > 0, и x °^pt = 0 иначе.

• 6.    Добавить полученное решение в текущую рабочую популяцию и продолжить работу ВГА.

ностей по формуле A P = ( A p j ) = ^ □ i ■ A P i .

i = 1

Основная идея данного алгоритма состоит в том, что вероятность на текущей популяции сравнивается с вероятностью на предыдущей популяции, а более поздние поколения (когда накоплено достаточно информации о поисковом пространстве) вносят больший вклад в прогноз оптимального значения гена, за счет выбора весовых коэффициентов. Весовые коэффициенты выбирают-NK ся таким образом, что о i+1 > a i и ^ a i = 1.

i = 1

Генетические алгоритмы условной оптимизации. В общем случае в ГА и ВГА выбор индивида из популяции происходит в зависимости от его степени пригодности – чем индивид бо-лее пригоден, тем у него больше шансов быть отобранным, при этом механизм учета ограничений оптимизационной задачи отсутствует. Можно использовать несколько возможных методов непосредственного решения этой проблемы.

Пусть решается следующая задача условной однокритериальной оптимизации:

• f ( x ) ^ extr;

g j ( x ) <  0, j = 1, r , _ h j ( x ) = 0, j = r + 1, m .

В общем виде пригодность индивида x вычисляется по формуле

• fitness( x ) = f ( x ) + 5 ■ Х ( t ) ■ £ f j ( x ),

j = 1

где t - номер текущего поколения; 5 = 1, если решается задача минимизации; 5 = -1, если решается задача максимизации; fj(x) – штраф за нарушение j-го ограничения; в - вещественное число. Штрафные функции fj (x) вычисляются по формуле max {0, gj (x)}, j = 1, r;

| h j ^{( x} )|, j = ^r + 1, m .

f, ^{( x} ) = •

Известны следующие штрафные методы: метод «смертельных» штрафов, метод статических штрафов, метод динамических штрафов, метод адаптивных штрафов, а также гибридные методы, использующие механизм «лечения».

После детального анализа каждого метода было принято решение использовать метод динамических и адаптивных штрафов, так как альтернативные методы обладают рядом недостатков.

В частности, метод «смертельных» штрафов попросту отбрасывает недопустимые решения, тогда как они, находясь вблизи допустимой области, зачастую несут в себе полезную информацию для порождения новых допустимых решений. Метод статических штрафов использует много настраиваемых параметров, которые пользователь должен самостоятельно подобрать перед решением каждой задачи. Неверный выбор данных параметров может привести к тому, что допустимые решения не будут найдены. Гибридные методы, использующие механизм «лечения», применяют на каждом шаге ЭА локальный поиск для того, чтобы минимизировать значения штрафных функций. Это требует значительных дополнительных вычислительных ресурсов.

Метод динамических штрафов. Данный метод использует штрафные функции, описанные выше, и определяет функцию Х ( t ) следующим образом:

Х( t) = ( C ■ t )a.

На t -й итерации пригодность индивида x вычисляется в данном методе по следующей формуле:

m fitness(x) = f (x) + Ц C ■ t )a ■^ fie (x).

i = 1

Параметры C , a, в подбираются индивидуально для каждой решаемой задачи. На практике рекомендованы значения C = 0,5; a = в = 2 (получено экспериментальным путем).

Метод адаптивных штрафов . Этот метод также использует вышеописанные штрафные функции, функция Х ( t ) вычисляется следующим образом:

i

Р1 ■ Х(t), если b е D, для всех t - к +1 < i < t,

Х(t +1) = jp2 -Х(t), если b е D, для всех t - к +1 < i < t,

Х ( t ), в остальных случаях.

где b - лучший индивид i- й популяции, р , е (0,1), р ₂ >  1 и Р 1 Р ₂ ^ 1. Здесь на ( t + 1)-м шаге происходит уменьшение штрафа, если лучший индивид в течение k предыдущих поколений принадлежал допустимой области. Если же лучший индивид в течение того же промежутка времени выходил за границы допустимой области, то происходит увеличение штрафа.

Метод вводит три дополнительных параметра Р1, Р2, k. Таким образом, метод адаптивных штрафов штрафует недопустимых индивидов не только в соответствии с тем, насколько они сами нарушают ограничения, но и с учетом того, насколько ограничения нарушались их предшественниками [7].

Вероятностный ГА условной оптимизации. Для задач условной оптимизации использование методов штрафных функций сохраняет общую схему использования ВГА, основная разница состоит в способе оценки решений – иначе определяется функция пригодности индивида. Аналогичным образом на задачи условной оптимизации распространяется и метод прогноза оптимальных решений в ВГА. Для прогноза ВГА целесообразно при- менять модифицированную процедуру прогноза, так как структура поверхности целевой функции «со штрафом» содержит большое число локальных оптимумов, и обычный прогноз на ранних итерациях вероятнее сойдется к локальному оптимуму, нежели к глобальному.

Численное исследование эффективности алгоритмов ГА и ВГА для задач условной оптимизации. Сравнение эффективности ГА и ВГА проводилось на множестве тестовых задач однокритериальной условной оптимизации. Целевые функции и ограничения в задачах представляют собой линейные и нелинейные функции нескольких переменных. Приведем здесь некоторые из задач, входящих в тестовый набор (табл. 1) [8].

Тестирование проводилось при наилучших и наихудших настройках параметров алгоритмов, для того чтобы установить диапазон влияния вносимых изменений на качество работы. Эти изменения могут и не улучшать работу алгоритма при наилучших настройках, но могут улучшать их при наихудших настройках, что дает положительный эффект в условиях произвольного выбора настроек неподготовленным в области эволюционной оптимизации пользователем.

Поскольку алгоритмы являются стохастическими, то для каждой комбинации параметров исследуемые характеристики усреднялись по 100 независимым запускам алгоритма.

В качестве исследуемых характеристик были выбраны следующие:

• –    процент запусков (%), в которых было найдено точное оптимальное решение;

• –    средний номер итерации ( N ), на которой впервые было найдено точное оптимальное решение.

На первом этапе исследования был определен метод учета ограничений, который является наиболее эффек-

Таблица 1

Тестовые задачи условной однокритериальной оптимизации

Условие задачи Известное решение 22 = x + y ^ max; y < 7 + sin(2 ■ x), y > 1 - sin(2 ■ x), x e[0,4] x = 4, y = 7,989 358 247, z* = 79,829 845 20 = 5 ■ x + 0,5 ■ y ^ max; y <-2 ■ x + 5, y > x - 1,5, y < 2 ■ x +1, x > 0, _ y > 0 13 x =—= 2,166 66, 6 y = 3 = 0,666 66, z* = — = 11,166 666 67 6 (x, y) = 2000x + 2400y ^ max; x > 0, y > 0, 120 + И0 < 1, 4x + y < 320, x + y < 110, + y < 1, 340 120 x + 2y < 160, ,x + 4y < 280 x = 50, y = 55, zopt = 232 000 n T /vx2       ГV cos(2n xt))     . = 20 + e - 20exp -0,2. > — - exp > --------— ^ min; ’ Vm N Ah N J V       ‘ =    J       v‘= N = 4; 2x - 3x2 + 4x3 < 10, 4 x 2 - 5 x3 + x4 < 1, 10x1 + 7,5x3 - 8,4x4 < 3,5, -3,1 x1 + 21,7x2 -36,4x4 < 16,2 x,- = 0, i = 1, N, zopt = 0 = M(0,1 ■ x2 -4cos(0,8xi) + 4) ^ min; N =' =2; x2 + 9x22 < 36, 9 x2 + x22 < 36 x, = 0, i = 1, N, zopt = 0 тивным для выбранного множества тестовых задач. В результате исследований было установлено, что для стандартного ГА при наилучших настройках динамический штраф оказывается эффективнее во всех случаях. При наихудших настройках динамический штраф эффективнее в 60 % случаев. В среднем, динамический штраф эффективнее адаптивного в 60 % случаев. Для ВГА динамический штраф оказывается эффективнее во всех случаях при наилучших и наихудших настройках.

Таким образом, было установлено, что для ГА и ВГА метод динамического штрафа является более эффективным, чем метод адаптивного штрафа.

На втором этапе исследования было проведено сравнение стандартного ГА и ВГА с использованием метода динамических штрафов для учета ограничений (табл. 2). При наилучших настройках стандартный ГА оказался эффективнее в 67 % случаев. Однако даже в тех случаях, когда ВГА уступает стандартному ГА, разница в эффективности незначительна. При наихудших и средних настройках наиболее эффективным оказался ВГА в 100 и 75 % случаев соответственно.

На третьем этапе исследования сравнивались стандартный ГА и ВГА с прогнозом (табл. 3). Было установлено, что при наилучших настройках ВГА с прогнозом в целом эффективнее ГА в 60 % случаев, а при наихудших настройках эффективнее в 67 % случаев. Кроме того, алгоритм с прогнозом находит оптимальное решение на более ранней стадии работы алгоритма.

Проведенные исследования позволяют сделать следующие выводы: для решения задач условной однокритериальной оптимизации ВГА более предпочтителен чем стандартный ГА, так как в среднем является более эффективным и при этом содержит меньшее число параметров для настройки, а алгоритм прогноза оптимального решения позволяет находить оптимальное решение на более ранней стадии работы алгоритма.