Об одной предельной квазистационарной задаче электрохимической обработки металлов

При электрохимической обработке металлов (ЭХО) изделие нужной формы и размеров получают путем обратного копированием формы электрода-инструмента (катода) за счет анодного растворения металла с поверхности заготовки (анода) [1].

Предельная электрохимическая обработка

Режим прекращения анодного растворения обрабатываемой поверхности при неподвижном катоде называется предельной электрохимической обработкой [2]. В этом случае, после прекращения активного процесса анодного растворения, формируется предельная анодная граница, на которой локальная плотность тока j_a достигает некоторого предельного значения j _пр. Величина j _пр зависит от различных параметров, в том числе от состава электролита, свойств обрабатываемого металла и определяется экспериментально.

Распределение плотности тока j_a на поверхности заготовки зависит от геометрии катода. В связи, с чем на поверхности заготовки можно выделить обрабатываемые участки, здесь межэлектродные зазоры малы и выполняется условие j a >  j _пр. И необрабатываемые участки, в точках которых из-за увеличения межэлектродных зазоров плотность тока убывает до значений меньших чем j _пр, и растворения металла прекращается.

Используя математическую модель предельного режима ЭХО, представленную в работе [2], рассмотрим двумерную задачу, связанную с определением конфигурации анодной границы при её обработке двугранным симметричным катодом. В модели задачи, в отличие от схемы, рассмотренной в работе [2], задается начальная форма поверхности заготовки, и выделяются ее обрабатываемые и необрабатываемые участки.

Об одной предельной квазистационарной задаче электрохимической обработки металлов

Миназетдинов Наиль Миргазиянович кандидат физико-математических наук, доцент, доцент кафедры информационных технологий и естественнонаучных дисциплин Российского нового университета, Москва. Сфера научных интересов: приложения методов теории струйных течений идеальной жидкости в задачах теории электрохимической обработки металлов. Автор 37 опубликованных научных работ.

Геометрия межэлектродного промежутка

Сечение катода координатной плоскостью x 1 , у 1 представляет симметричный угол DCD 1 (рис. 1а). Система координат x 1 , у 1 связана с катодом, а ее начало совпадает с вершиной C . Ось симметрии катода совпадает с осью ординат. Углы наклона лучей CD и CD 1 относительно оси абсцисс характеризуются величиной а . Перед началом процесса электрохимического формообразования анодная граница описывается прямой DBD 1 . Начальная величина межэлектродного зазора в сечении CB равна S 1 .

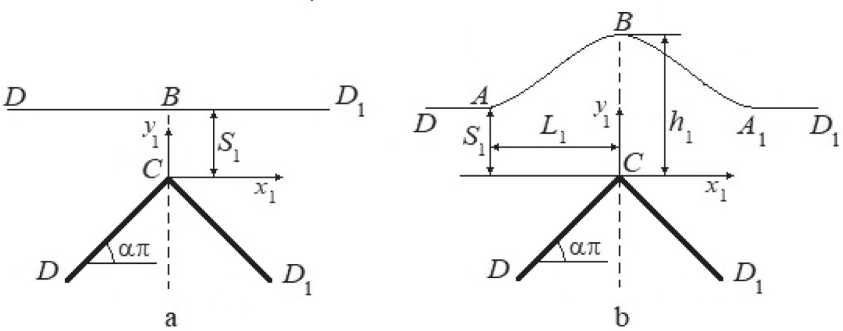
Рис. 1. Геометрия межэлектродного промежутка. а – до начала процесса обработки; b – получаемая в процессе обработки.

В процессе обработки формируется предельная анодная граница, состоящая из обработанного участка AA 1 , на которой выполняется условие j a = j cr и необрабатываемых участков AD и A 1 D 1 (рис. 1b), параллельных оси абсцисс. Ординаты точек A и A 1 равны $ ! . Межэлектродный зазор в сечение CB равен h 1 . Половина ширины обработанного участка равна L 1 . Далее, в силу симметрии межэлектродного промежутка относительно оси ординат, ограничимся рассмотрением ее левой симметричной части.

Численно-аналитический метод решения задачи

Введём аналитическую функцию W 1 ( z 1 ) = v ( x 1 , у 1 ) + iu ( x 1 , у 1 ) комплексной переменной z 1 = x 1 + iy 1 . Действительная часть v ( x 1 , у 1 ) соответствует функции тока, а мнимая часть u ( x 1 , у 1 ) - потенциалу электрического поля [3]. Потенциал u ( x 1 , у 1 ) принимает постоянные значения на границах электродов

Методы обработки данных uDAB = ua , uCD = uc .

На искомой границе AB выполняется условие

• _ d U _ .

ja = K~Z.   = jпр , d n1

здесь производная в направлении внешней к области межэлектродного проме- d n 1

жутка нормали к анодной поверхности АВ ; к - удельная электропроводность среды.

На оси симметрии BC линия тока электрического поля, ортогональна к её эквипотенциальным линиям, и функция v (x 1, y 1) принимает постоянное значение. Можно считать, что на линии ВС функция v(x 1, y 1) равна нулю vBC = 0.

В соотношениях (1) – (3) произведем замену [2]

( u — uc )

y =7----- 7, Ф^=-j—

( u a ^— u c )       ( u a

v

—

z

—- , z = — = x + iy , u c )      H

_тг ^{к (} u a ^— u c )

где H =--------- - характерный размер длины; ф(x,y) и y(x,y) гармонически со- j пр пряженные функции [3].

—

Задача сводится к определению формы границы AB при выполнении следующих условий для безразмерного комплексного потенциала W ( z ) = ф ( x , y ) + г у ( x , y ) электрического поля

V dab = ¹, ^y cd = ⁰ .

^ddy \ = 1, ^d n ) AB

Ф вс = ⁰ .

Область изменения переменной W представлена на рисунке 2a.

Рассматриваемая задача электрохимической обработки при ее гидродинамической интерпретации [2] равносильна задаче по определению свободной поверхности фиктивного плоскопараллельного течения идеальной несжимаемой жидкости, текущей около заданной поверхности [4]. Поток направлен от источника, расположенного в бесконечно удаленной точке D , к стокам, непрерывно распределенными вдоль линии BC .

dW 5ф ,5y

Если ввести функцию ---=--+ г---= Vx — zVy = Ve dz dx dx         y

г 0

, где V величина скорости

фиктивного течения, 0 - угол, образуемый вектором скорости в какой-нибудь точке плоскости течения с осью абсцисс, то согласно равенству (6), на границе AB скорость фиктивного течения удовлетворяет условию [4]

dW dz

AB

= V = 1.

Вдоль границы AD скорость монотонно уменьшается от значения V = 1 в точке А до

нуля в точке D .

Об одной предельной квазистационарной задаче электрохимической обработки металлов

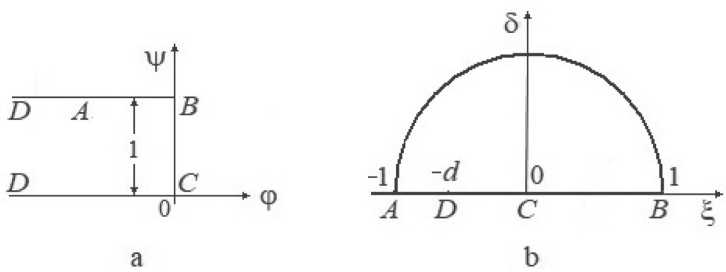
Рис. 2. Вспомогательные области:

а) область изменения комплексного потенциала W ;

b) область изменения вспомогательной переменной t .

Для построения функций, определяющих решение задачи, введем параметрическую комплексную переменную t = ^ + i 5 , изменяющуюся в области G t ( И<^> ^ >0 ) (рис. 2b).

Согласно условиям (5), (7), функция W ( t ) = ф ( t ) + i y ( t ) удовлетворяет граничным условиям

1, t = exp ( i o ) , o e [ 0, n ] ,

^ ( t ) = < 1, t = ^ ,         ^ e [ - 1, - d ) ,

_ 0, t = ^ ,         ^ e ( - d ,0 ] ,

^ ( ^ ) = 0, ^ e [ 0,1 ] .

Используя метод конформных отображений [3], получим dW лт t +1 лт (1 + d) Vd = N —j=------------, N = -------- dt       tit (t + d)(1 + d • t)            n

Введем функцию [4]

x ( t ) = In | d^- | = In V - i 9 , <  dz J

На границе области G t функция x ( t ) удовлетворяет условиям

Re x ( exp ( i o ) ) = 0, c re[ 0, n ] ,

⁰, ^ e[ ^- 1, ^- d ) ,

Im / ( ^ ) = - # ( £ ) = *-ап, £ е ( - d , 0 ) , 0 И0,1 ] .

Функция % ( t ) имеет логарифмические особенности в точках C ( t = 0 ) , D ( t = - d ) .

Применяя метод особых точек Чаплыгина [4], найдем

t + d

х ( t ) = a ^"7;—ГТ".

^v '         t ( 1 + d • t )

Используя формулы (10), (14) и равенство

Методы обработки данных dz = exp(-z(t))dWdt,                          (15)

dt установим соответствие между плоскостью переменной z и областью Gt . При условии, что образ точки t (C) = 0 переходит в начало координат плоскости z, это соответствие задается формулой

z ( t ) = N t F ( т ) d т , F ( т ) =----------- ^ +1--------— .        (16)

^J 0                 т⁰-^5- “ (т + d )^{a + 1} ( 1 + d rV

Формула (16) позволяет определить геометрические параметры межэлектродного промежутка.

Безразмерная величина межэлектродного зазора в сечение BC равна

h h = — = Imz (1).                         (17)

Координаты точек анодной границы AB найдем с помощью формулы

z ( e i ) = z ( 1 ) + Ni J F ( e^{l a} ) e ⁿ d a , 0 <  у <  n .                (18)

L S

Безразмерные координаты точки A равны x_A = - — = - L , y A = — = S (рис. 1b), тогда

L = — Re z ( — 1 ) ,

S = Im z ( - 1 ) .

Предельная квазистационарная задача электрохимической обработки

Предположим, что катод совершает поступательное перемещение в сторону обрабатываемой заготовки с постоянной скоростью Vc. Величина сдвига А1 катода за время T, от носительно ее исходного положения, равна А1 = VcT . Задачи, связанные с определением предельной анодной границы в момент времени T = —1 или после совершения катодом Vc сдвига А1, называются предельно квазистационарными [5].

Безразмерная величина А перемещения катода относительно ее исходного положе ния за время T равна А =

H = ^К ( u a ^- u c )

VcT c . Если в качестве характерного времени выбрать величину

Vc     (jпр Vc ) ,

то можно ввести в рассмотрение безразмерное время т [5]

VcT     jïðVc т                 / XT ,

H    ^к ( u a ^- u c )

Рассмотрим двумерную предельную квазистационарную задачу электрохимической обработки двугранным симметричным катодом, сечение которого представлено на рисунке 1a. Левая симметричная часть межэлектродного промежутка представлена на рисунке 3: на ней CD – граница катода, BC – ось симметрии, AB – обрабатываемый участок анодный границы, AD – необрабатываемый участок.

Об одной предельной квазистационарной задаче электрохимической обработки металлов

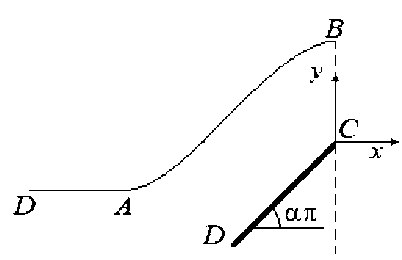
Рис. 3. Геометрия межэлектродного промежутка

Формулы, полученные при решении рассмотренной задачи электрохимической обработки неподвижным катодом, остаются в силе, за исключением формулы (20).

С учетом безразмерного сдвига А катода относительно его исходного положения, определяемого величиной S , безразмерная ордината точки A в системе координат, связанной с катодом равна

У а = S - т .                                (25)

Используя формулу (25), соотношение (20) представим в виде

S - т = Im ( z ( — 1 ) ) .                               (26)

Для численного решения задачи задаются геометрические величины а , S и безразмерное время т . Параметр d определяется из условия (26). Величины h , L и координаты точек предельной анодной границы определяются с помощью формул (17)-(19).

Результаты расчётов

В качестве примера рассмотрим случай, когда а = 0,25 и S = 0,05. В таблице 1 представлены результаты расчетов безразмерных геометрических характеристик: h , L , y_A и математического параметра d для различных значений т .

Таблица 1

Результаты расчета параметров

т	h	L	y A	d
0	0,638	1,728	0,05	0,801
1	0,623	2,831	- 0,95	0,978
2	0,621	3,843	- 1,95	0,998
2,5	0,621	4,343	- 2,45	0,999

На рисунке 4 представлены графики анодных границ для указанных случаев.

Выполнены расчеты анодной границы при фиксированных значениях S = 0,1 и т = 1 для различных значений а. В таблице 2 представлены результаты расчетов геометриче- ских характеристик для следующих значений параметра а:"^’"^’"^’^•

Методы обработки данных

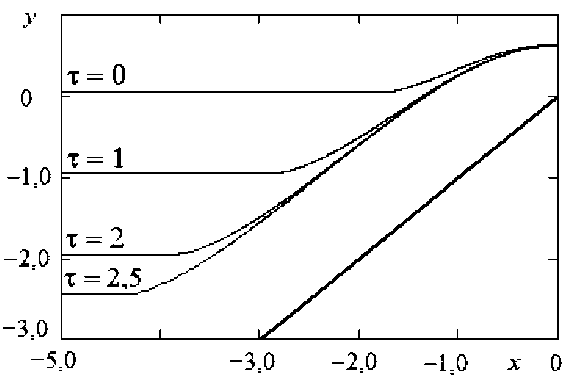
Рис. 4. Результаты расчета анодных границ.

Таблица 2

Результаты расчета параметров

α	h	L	y A	d
1 6	0,714	4,015	-0,9	0,996
1 4	0,623	2,779	- 0,9	0,975
1 3	0,553	2,146	- 0,9	0,940
1 2	0,456	1,477	- 0,9	0,861

На рисунке 5 приведены графики обработанных участков анодных границ для указанных значений.

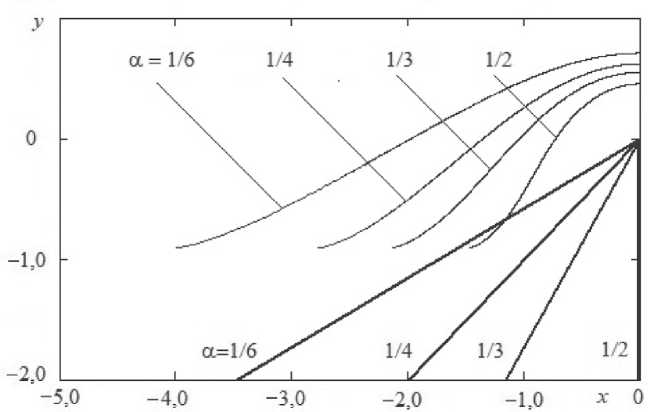
Рис. 5. Результаты расчета анодных границ.

Об одной предельной квазистационарной задаче электрохимической обработки металлов

Заключение

В работе представлено решение и результаты расчетов конкретной предельно-квази-стационарной задачи теории электрохимической обработки металлов. Связь времени и величины сдвига катода, относительно ее исходного положения, позволяет определить форму предельной анодной границы в различные моменты времени.