Об одной сходимость по вариации двумерного распределения Романовского

В статье [3] изучены одно асимптотическое свойство двумерного распределения Романовского :

Р(^1 = Р^2=Т)= ^N,M,n (Р,Т =

ч

р Л!     рП    pj—-?n — l

^-m+i ^ п+у '-‘N+M—m—/Л.—Г1—2

N

-N+M

0,

если pi,] = 0,М p + ] = 0,М если pi,] > М    pi,] < 0

полученного из изучения двух упорядоченных выборок произвольных объемов N и M :

x_x <  x ₂< ... <  x_N

У 1 <  y 2 < ... <  У м  ( M >  1, N >  1)

из одной и той же непрерывной совокупности S c плотностью f ( x ) , которая нам неизвестно. В первой выборке выделяя в ней член x , мы будем иметь n членов её , которые не более х_п+1 и N - n -1 членов её , которые не менее х_п+1.

В этой работе В. И.Романовского найдено вероятность того , что во второй выборке будет ц членов её , которые не более х_{п+ х}, и M - д членов её , более x :

x₁ <  x ₂< ... <  x_N

У 1 <  У 2 <  ... <  У м      ⁽ N >  1, M >  1)

т.е. доказана теорема о сходимости по вариации двумерного распределения Романовского к сверткам одномерных распределений Пуассона и нормального распределения. А в этой статье изучаем еще одно свойство двумерного распределения Романовского, а именно

Теорема. Пусть M ^ да, а ^ да, p ^ 0, тогда да да

ХХ | R ⁽ д , П ) -П ₁ ( д ⁾ П 2⁽ п ) | = / ... ( г /. + p ) + O ^а 2 + p ²⁾

д = 1 п = 1

Здесь

П 1 ( д ) =

( N - n - 1

kq     ⁿ q

Р )      Р

( N - n - 1)!

exp <

kq . Р

,

k = 1,2,...

-бэта - распределение,

П2(П)=

---1= exp 1

О ^2П

д - nq

°q

-нормальное распределение.

Доказательство. Обозначим через $ и  $2    суммы индексы

суммирования д и п которых, удовлетворяют неравенству $ 1 <  О •   ^ 2 >  О ч   ^{( о} 0 = ^min( ^ д , & п ))

Оцениваем $. Для этого нам нужны да да Л

XX д

д = 0 п = 0 V

mp

q J

z дада

П,(д)П2(п) =Хп2(п)Х д

П = 0          д = 0 V

mp

q J

П 1 ( д )

=3а2A2qM2+(16ав+21ав - 19ав2+ав3)м

От последнего можно получить

„                  „ (и ²+v²->²                  ( 1 'I

X П , ( д ) П 2 ( п ) <  X (—аП 1 ( д ) П 2 ( п ) = O -2

и ² + V ² > о 0                   и ² + V ² > о    О)                          V а J

Точно также получаем

r1 ^

^ £

X R ( a ) + 2 .  2.

u + V > ^ 0

S П1(а)П2(п) = O — u2 + v2>o-0                         \ ^0 J

Для сумм удовлетворяющие u2 + v2 < ^ имеем w w

S 1 = X3d( A , n ) - 1| П 1 ( а ) П 2 ( п )

a = 0 п = 0

где d (АП) =

R (АЛ) П1(а) -П2(п)

(1)    преобразуем

(N + M - n - m - а -П)!   N!M!   (n + П)!  (m + а)!

R ( АЛ ) =  ---------------— ^х------^х  ---— ^х  ---^~ ^х

( M - а -П )!      ( N + M )!    ^п W      m !

( N - n - m )

( N - n - m )

х I _o х I х I ₂ х I ₃ х I₄

(N + M - n - m - a - п)(N + M - n - m - a - П -1)

Здесь I _o, | , I ₂, I ₃ определяются следующим образом:

I _ ( N + M - n - m - а -П )! j _ N ! M !     _( n + п )!

⁰ =       ( M - a - П )!      • ¹ ” ( N + M )!.  ² = n Л !  • т ₌ ^{( m +} A ^)!

;                               ’                              ;    I 3

m !

_                ( N - n - m )

4 = (N + M - n - m - а-П)(N + M - n - m - a - П -1)

mp

A = — 1 + q .

u (1 - a - a )

A

;

m - a - n=m (1 - a - a) х 1

u a

va.

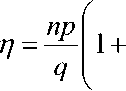
v (1 - a - a ) ^v ^ ^- r² ^ 2

N - n - m = N (1 - a - a)

Из условия теоремы N ^ w, M ^ w, n ^ w, m ^w и так как переменные u, v ограниченны можно использовать формулу Стирлинга для Ir, I2, I3 . После нетрудных вычислений имеем w w

$ 1 = SI I ^d( АЛ ) ^- 1 ^П 1⁽ A ^{) n} 2⁽ П ) =

А = 0 и = 0

w w

=zz

A = 0 и = 0

R ⁽ A , n ) ^П 1⁽ А ^{) П} 2⁽ П )

—

1П(а)П(п) = Л (a + Р) + O(a2 + p2) + O

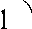
Последнее равенство показывает верность теоремы.