Об одной задаче численного секционирования в офтальмологии

Важной задачей, возникающей в офтальмологии, является неинвазивное восстановление изображения 3-мерной структуры различных отделов глаза (например, сетчатки) для последующей диагностики их заболеваний. Наиболее распространённым заболеванием сетчатки в мире на сегодня является диабетическая ретинопатия, которая служит основной причиной необратимой слепоты в развитых странах мира [1]. В клинических условиях активность ретинопатии оценивают по параметрам офтальмоскопической картины, толщины сетчатки, сосудистых изменений сетчатки, количеству микроаневризм, экссудатов и кровоизлияний. В большинстве случаев современная диагностика ретинопатий основана на классических способах офтальмоскопии или фоторегистрации изображений сетчатки в видимом спектре, а при дифференциальном диагнозе типа ретинопатии применяют флюоресцентную ангиографию [2]. Метод оптической когерентной томографии [3] также приобретает популярность в качестве альтернативной флюоресцентной ангиографии малоинвазивной методики изучения микроструктуры сетчатки. При этом трёхмерная реконструкция изучаемого участка программным методом реализована лишь в нескольких моделях оптических когерентных томографов сетчатки, а получаемые томограммы не позволяют исследователю в полной мере оценить ангиоархитектонику сетчатки. Кроме того, сосуды сетчатки, лежащие на её поверхности, имеют гиперрефлективные свойства, затрудняя оценку расположенной под ними ткани сетчатки. Также приходится учитывать и соответствующим образом компенсировать артефакты типа разрыва участков изображения, вызванные движением живого глаза [4]. В этой связи быстрая трёхмерная деконволюция сосудов с последующей трёхмерной реконструкцией прилегающей ткани может оказаться превосходящей по информативности клинической методикой оценки экссудативных форм ретинопатии.

Один из перспективных методов восстановления основан на быстрой перефокусировке изображающей системы, например с использованием методов адаптивной оптики [5], для получения стека изображений глазного дна, находящихся на различной глубине, с последующим восстановлением трёхмерной структуры известными методами. Получающиеся на этом пути изображения в каждой фокальной плоскости представляют собой суперпозицию истинного сечения трёхмерного объекта в данной фокальной плоскости с размытыми изображениями соседних по глубине сечений. Кроме того, типичной является ситуация, при которой на истинное изображение в фокальной плоскости накладываются аберрации оптической системы глаза, флуктуации фиксации, а при его регистрации приходится также учитывать искажения светочувствительных сенсоров. Таким образом, возникает проблема устойчивого к помехам получения «очищенного» от указанных искажений стека изображений сечений глазного дна по глубине для его последующего использования в трёхмерной реконструкции.

Известным аналогом данного подхода является метод цифрового секционирования в биомикроскопии (см., например, [6]; [7], гл. 22; [8], гл. 14). В приближении полностью некогерентной изопланарной оптической системы изображение трёхмерного объекта описывается уравнением i (x, y, z) = o (x, y, z) * h (x, y, z), (1) где i(x, y, z) – наблюдаемое изображение (интенсивность), o(x, y, z) – искомый объект, h(x, y, z) – трёхмерная функция точечного источника (point spread function, PSF), * – знак операции трёхмерной свёртки. С помощью известной теоремы о свёртке связь между искомым объектом и его изображением в Фурье-пространстве записывается в виде поточечного произведения

I ( u, v, w ) = O ( u, v, w ) • H ( u , v, w ) (2)

соответствующих 3D фурье-образов I, O, H от функций i, o, h . Однако даже в идеальном случае, когда наблюдаемое изображение и функция точечного источника известны точно, однозначное нахождение фурье-образа O искомого объекта о из уравнения (2) затруднительно вследствие возможного обращения в ноль (или близости к нулю) мультипликатора H ( u , v , w ) в некоторых точках. Ситуация ещё более усложняется при работе с реальными данными эксперимента, когда в распоряжении имеются результаты наблюдения в конечном наборе секущих плоскостей z е { z 1 ,z ₂, . , z_N }, при этом как сами измерения, так и функция точечного источника, как правило, известны лишь приближённо. В этой связи особое значение имеет разработка специальных устойчивых методов решения уравнения вида (1), которые бы в наилучшей степени учитывали как специфику физической постановки задачи, связанной с характерными особенностями функции точечного источника рассматриваемой оптической системы глаза, так и требуемое соотношение производительность / точность в условиях реальных искажений, типичных для рассматриваемого класса задач офтальмологии.

ства ресурсоёмких вычислений обычно предполагается [6], что только ближайшие p (как правило, p = 1), лежащие снизу и сверху, соседние плоскости вносят существенный вклад в формирование изображения i m . Кроме того, рассматриваются только эффекты, вызванные дефокусировкой, причём игнорируется её влияние для функции точечного источника в фокальной плоскости, т.е. предполагается, что h ₀- дельта -функция Дирака. В результате получается приближённое соотношение

о = i mm

V     о

^Z       o n  ^ п - m .

n = m ± 1, m ± 2, . , m ± p

Поскольку под знаком суммы искомые функции o n также неизвестны, то в простейшем случае используются их аппроксимации вида

о = c i m 2 m

C Z n = m ± 1, m ± 2, . ,i

( i n * f ) h n - j , m ± p

1. Постановка задачи и метод решения

Конкретизируем постановку задачи, связанную с отмеченной выше спецификой. Поскольку для обработки доступны сечения трёхмерного изображения глазного дна лишь в конечном наборе плоскостей, задаваемых его сечениями при z е { z 1 , z ₂,..., z N }, причём количество таких сечений (10-15), как правило, на порядки меньше количества точек в каждом горизонтальном сечении, то имеет смысл перейти от симметричной по координатам ( x , y , z ) формы записи уравнения (1) к её дискретному по z аналогу следующего вида:

с эмпирически подбираемыми коэффициентами c _1,2, отвечающими за относительный вклад информации из фокальной и соседних плоскостей в формирование изображения, и высокочастотным фильтром f , который убирает низкочастотную информацию из областей размытия. Для повышения точности вычислений также используются итерационные варианты (3) и (4), при этом для сокращения вычислений итерации проводятся в фурье-образах. Например, итерационный аналог (4) имеет вид [6]:

О ⁽ k ^{+ 1)} = c,\I m 2 m

c1       Z       onk) • Hn-jl, n=m ±1, m ±2,., m ± p              )

k = 0,1, . ,       o n ⁰’ = I n.

i m = i ⁽ x , У , z m ) = o m * h 0 ⁺

+ Z n * m o ( X , У , z n ) * h n - m ( x , У ), m = 1,2, . , N ,

где * - знак операции двумерной свёртки, h_n-m ( x , y ) = = h ( x , y , z_n - z_m ) A z . Нетрудно видеть, что с помощью уравнения (3) фактически описывается ситуация, в которой искомый достаточно тонкий объект аппроксимируется с помощью стека секущих плоскостей z = z m , расположенных на одинаковом расстоянии A z друг относительно друга, что приводит к соответствующей аппроксимации интеграла свёртки по переменной z . Уравнение (3) связывает наблюдаемое в плоскости z m изображение i_m с входящими в сумму изображением o_m * h ₀ искомого объекта в фокальной плоскости и дефокусированными изображениями от соседних плоскостей z n +z m . Отметим, что уравнение (3) может использоваться также и вне связи с трёхмерной моделью (1), например, для моделирования трёхмерной изображающей системы со слоистой полупрозрачной структурой [9], причём толщина слоёв может быть различной.

Заметим, что при решении задачи секционирования в биомикроскопии в целях уменьшения количе-

Описанные методы (4), (5) отличаются простотой реализации и хорошо зарекомендовали себя для сравнительно грубой деконволюции в задачах флуоресцентной биологической микроскопии. Однако для задачи секционирования изображений отделов глазного дна, как отмечалось выше, приходится учитывать аберрации оптической системы глаза, флуктуации фиксации, а также учитывать помехи регистрирующих устройств, что приводит к необходимости разработки специальных устойчивых методов решения уравнения вида (3) в полной постановке, что предъявляет жёсткие ограничения на соотношение производительность / точность для рассматриваемого класса задач офтальмологии.

Хорошо известно, что задачи секционирования и деконволюции трёхмерных объектов являются весьма затратными относительно вычислительных ресурсов [6]. Поэтому большую роль играет выбор экономичных алгоритмов, использующих новейшие компьютерные технологии (см., например, [10], [11]). Имея в виду широкие возможности реализации идей распараллеливания алгоритмов на современных многопроцессорных системах (CPU или GPU), рассмотрим вытекающее из (3) соотношение, которое связывает соответствующие двумерные Фурье-образы

I m , O n , H n функций i , o , h в плоскости спектральных переменных ( u , v ):

N

I m ⁽ u , ^v ) = S O n ⁽ u , ^v ) • H n - m ⁽ u , ^v), m = ^1,2, . ^, N .    ⁽⁶⁾

n = 1

Таким образом, в каждой точке ( u , v ) Фурье-плоскости уравнение (6) задаёт систему линейных алгебраических уравнений (СЛАУ) с матрицей S размера N х N относительно вектора коэффициентов Фурье O = O ( u , v ) = ( O 1 ( u , v ), O ₂( u , v ), . , O N ( u , v )) искомого объекта, которую, опуская параметры ( u , v ), можно записать в виде

SO = I , I = ( 1 1 , 1 2,..., I n ).                           (7)

Типичная для рассматриваемых прикладных задач ситуация состоит в том, что, несмотря на относительно небольшую размерность матрицы S, точно обратить её либо нельзя из-за нетривиального ядра, либо нецелесообразно из-за вычислительных ошибок.

Рассмотрим неявный итерационный метод для устойчивого нахождения решения СЛАУ (7) (см., например, [12] гл. 2; [13] гл. 2, п. 5). В обозначениях (7) метод зависит от параметра ц > 0:

O⁽ k ^{+ 1)} = ( E + ц S * S ) ^{- 1} O⁽ k ) + ц ( E + p S * S ) ^{- 1} S * I , - (0)                                   ⁽⁸⁾

к = 1,2, . , O = (0,0, . ,0).

В [12] гл. 2 показано, что (8) задаёт регуляризирую-щий алгоритм (РА). В связи с этим отметим, что первая итерация метода (8) в сочетании с дополнительным правилом выбора параметра ц приводит к классическому методу регуляризации А.Н.Тихонова [14], что позволяет делать выводы о роли этого параметра.

Отметим, что метод (8) в терминологии ([12], гл. 5) относится к классу так называемых псевдоите-рационных методов. При соответствующей организации вычислительного процесса итерации можно реализовать в виде умножения на соответствующие степени матриц перехода в Фурье-плоскости. Это позволяет существенно экономить машинное время в ситуации, когда входные данные заданы с высокой точностью и, следовательно, получение соответствующего приближённого решения потребовало бы большого числа итераций. Кроме того, поскольку процесс (8) должен быть реализован в каждой точке выбранной области Фурье-плоскости, то в целом описанный подход допускает естественное и эффективное распараллеливание вычислительного алгоритма при использовании многоядерной структуры современных CPU и GPU.

• 2.    Функция точечного источника

Остановимся подробнее на виде используемой PSF. В наиболее простой постановке источником изображения являются N полупрозрачных слоёв, отстоящих друг от друга на расстояние A z вдоль оптической оси. При точной фокусировке системы на один из слоёв возникает расфокусировка других сло-

ёв. Если апертура системы имеет характерный размер 2 r , фокусное расстояние f то дефокусировка слоя, смещённого на расстояние A z << f, равна D = A z / f ² , а соответствующая стрелка прогиба на апертуре 2 r равна d = ( A z /2)х( r / f ) ² . При этом степень размытия определяется фазовым сдвигом p s ( x , y , A z_nm ) и зависит от удалённости от плоскости фокусировки:

• / л ч J x ² + У ² 2 n

Ps (x, У, Aznm ) = dnm ---2--Г = r л

• = 0,375n( x ² + y ²) | n - m\ ,

• 3.    Результаты секционирования объекта «Секторы»

A z r²

nm dnm = 2 f 2 ’ где n - номер слоя, вклад которого учитывается при фокусировке на слое с номером m, Aznm - смещение слоя n относительно слоя m. Глубина объекта по координате z составляла 300 микрон. Расстояние между соседними слоями для случая стека из N = 5 секущих плоскостей тестовых изображений составляло 300/(N -1) = 75 микрон. Остальные параметры: % = 0,5 микрон, f=20 мм. Также в модели учитываются аберрации второго порядка p(x,y) = 0,5п(x2+ y2), не зависящие от номера плоскости. Таким образом, PSF изображающей системы в рассматриваемом случае принимает вид

h ⁽ x , y , z n ^- z m ) =

= F ⁽ M ⁽ x , y ) • exp ^{i • P s ⁽ x , y , ^{A z} nm ) + i • p ⁽ x , y ^)})| ² , где F - оператор двумерного преобразования Фурье, i ² = -1. Отметим, что наличие зрачка в рассматриваемой оптической системе учитывается с помощью функции зрачка M ( x , y ), которая задаётся индикаторной функцией круга радиуса r :

M ( x , y ) = ind ( x ² + y ² <  r ² ) .

Рассмотрим тестовый объект «Секторы», который представляет собой трёхмерную структуру из пяти плоскостей, в каждой из которых расположено изображение секторов, но повёрнутое в каждой плоскости на определённый угол (см. рис. 1 а). Поскольку в рамках принятого приближения и в силу симметрии объекта в равноудалённых от центральной плоскости сечениях наблюдаются качественно схожие результаты, далее приводятся изображения только для слоя m = 2. Присутствие пространственно-однородных областей, характеризуемых различными пространственными масштабами, в сочетании с резкими переходами интенсивности приводят к широкому использованию такого рода объектов для тестирования качества различных методов деконволюции, и в частном случае секционирования. Наблюдаемое изображение при фокусировке в каждую плоскость состоит из исходного изображения, искажённого аберрациями второго порядка, и дефокусированных изображений из остальных плоскостей. В результате на рис. 1б хорошо видны искажения, связанные с размытием и наложением изображений, а также частичной инверсией интенсивности.

а)

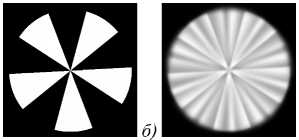
Рис. 1. Исходное сечение объекта «Секторы» (а) и наблюдаемое изображение сечения (б) в секущей плоскости m = 2

Задача секционирования состоит в восстановлении исходных изображений в каждой плоскости. Рассмотрим результаты работы неявного итерационного метода без шума в зависимости от параметров метода – коэффициента ц и количества итераций K. Эксперименты показали, что при ц >0,1 восстановленное изображение получается излишне сглаженным. Рассмотрим полученные результаты при ц = 0,1 (см. рис. 2) на примере слоя m =2. Видно, что увеличение числа итераций приводит к улучшению качества восстановления. Вместе с тем следует отметить эффект «насыщения», когда дальнейшие итерации метода (более 40) уже перестают оказывать существенный вклад в улучшение изображений. Аналогичная картина наблюдалась и при других значениях параметра ц.

K = 5            K = 10            K = 40

Рис. 2. Зависимость от K ( ц = 0,1 ,т = 2 )

Уменьшение параметра ц в целом приводит к ухудшению качества восстановления вследствие усиления эффекта Гиббса («ringing effect») на контрастных границах объекта и вследствие этого нецелесообразно. Сравнение результатов секционирования при фиксированном числе итераций при разных ц показывает, что наилучшие результаты получаются при ц = 0,1 и 40 итерациях (см. рис. 3), а увеличение итераций не даёт эффекта, как и выбор других значений ц .

Рассмотрим особенности секционирования, когда на вход методу подаются дефокусированные изображения с аддитивным Гауссовым шумом порядка 1 % либо с пуассоновским шумом порядка 2 %, что соответствует порядка 100000 фотонов единичной интенсивности пикселя.

Характерно, что шум практически не заметен на фоне исходных дефокусированных изображений с соседних плоскостей (рис. 4 а , б ). Однако наличие шума влияет на качество секционирования.

На примере секционирования второго слоя рассмотрим влияние шума на качество работы алгоритма в зависимости от числа итераций при разных зна- чениях параметра ц. Из анализа рис. 5 видно, что, в отличие от случая без шума, с увеличением числа итераций восстановление может ухудшаться. Количество итераций должно быть согласовано с уровнем шума для получения приемлемых результатов: в рассматриваемом случае достаточно ограничиться 40

итерациями.

ц =0,1

ц = 0,01

Рис. 3. Результаты секционирования слоя m = 2 при K = 40 и различных ц

ц = 0,001

Рис. 4. Дефокусированные изображения слоя m = 2

а)

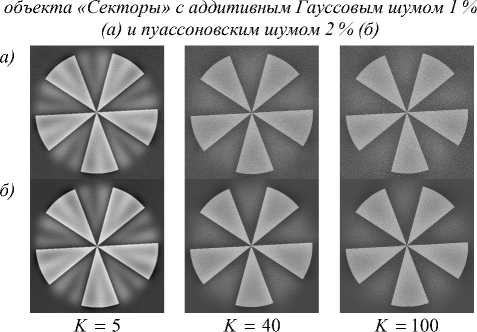
Рис. 5. Зависимость от K ( ц = 0,1 , слой m = 2 ) в случае

Гауссова шума 1 % (а) и пуассоновского шума 2 % (б)

Аналогичные выводы справедливы и для значения параметра ц = 0,01. Однако надо иметь в виду, что при уменьшении параметра ц качество секциониро-

Рис. 6. Зависимость от ц (K = 40 , слой m = 2 ) в случае

Гауссова шума 1 % (а) и пуассоновского шума 2 % (б)

Таким образом, возможности выбора параметра ц для подстройки работы метода к специфике восстанавливаемых изображений и искажений ограничиваются при малых ц эффектом Гиббса, приводящим к ложному оконтуриванию, однако это может быть важно в задаче выделения контуров изображений при априорной информации об однородности изображения между контурами.

• 4.    Секционирование изображений глазного дна

Для работы с изображениями глазного дна рассматривался стек из N =3 секущих плоскостей объекта (см. рис. 7 а ) с глубиной 200 микрон по координате z . Заметим, что, в отличие от объекта «Секторы», в рассматриваемом случае существенно больше полутонов и актуальных для диагностики патологий вы-

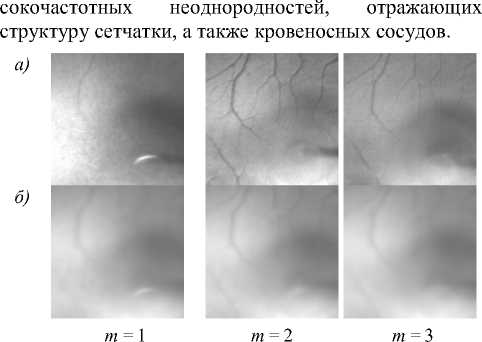
Рис. 7. Исходные изображения глазного дна (а) и стек наблюдаемых изображений без шума (б)

Соответствующие функции дефокуса между плоскостями и аберрации второго порядка имели вид:

Ps (x, y, Xznm) = 0,5n( x2 + y2) | n - m|, p (x, y) = 0,5n( x2 + y2).

В каждой плоскости фокусировки вместо исходных изображений наблюдаются результаты их конво-люции с изображениями соседних плоскостей в сочетании с общими аберрациями второго порядка. Соответствующие изображения, приведённые на рис. 7 б , характеризуются сильным размытием и исчезновением структуры сетчатки.

Для количественной оценки качества восстановления изображений в каждой секущей плоскости фокусировки используется векторный частотный критерий (ВЧК), позволяющий контролировать особенности восстановления в спектральной плоскости и задаваемый функцией

A ( r ) = — m ( r )

∑

( u , v ): r ² < u ² + v ² < ( r + 1)²

F ( E ( D ( 3 )) ) F ( E ( D ( о )) )

( u , v ),

где o~ – восстановленное изображение, сдвинутое в неотрицательную область, o – исходное изображение, D (X) = X/D(X), E (X) = X/E(X), D(•) - дисперсия, E(•) - среднее, m(r) - число точек (u, v), удовлетво- ряющих соотношению r2 ≤ u2+ v2 ≤ (r+1)2. Таким образом, для вычисления ВЧК сравниваемые изображения нормируются на свои средние по апертуре значения и на дисперсию. Далее вычисляются Фурье-образы и находится отношение их модулей. Полученное распреде- ление усредняется по концентрическим кольцам с центром в нуле шириной в несколько пикселей (в наших экспериментах – 2). Составленная из полученных значений результирующая кривая даёт зависимость нормированного отношения спектров от модуля спектральной переменной в относительных единицах и позволяет охарактеризовать результаты восстановления в зависимости от интересующей частотной области.

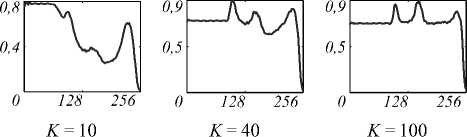
Рис. 8. Результаты секционирования слоя изображений глазного дна и ВЧК в зависимости от K

( ц = 0,1 , слой m = 2 без шума)

Как и в случае объекта «Секторы», при обработке реальных изображений глазного дна без шумов при увеличении количества итераций наблюдается эффект «насыщения»: дополнительные (после 40) итерации уже визуально не заметны (см. рис. 8). Однако применение ВЧК позволило выяснить, что на больших итерациях метод отрабатывает в основном высокочастотные составляющие изображений, приближая ВЧК к равномерному распределению.

При уменьшении параметра ц до значения 0,01 ухудшается качество восстановления высокочастотных составляющих изображения. Увеличение количества итераций (не менее 100) частично исправляет ситуацию, однако неравномерность векторного критерия выше по сравнению с ц = 0,1. В связи с этим дальнейшее уменьшение ц нецелесообразно вследствие ухудшения равномерности ВЧК и появления эффекта Гиббса (см. рис. 9).

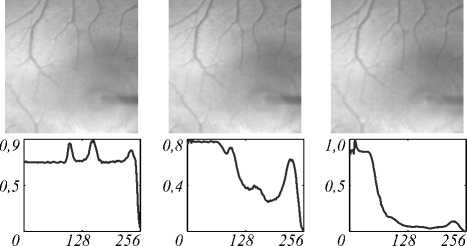
ц = 0,1              ц = 0,01             ц = 0,001

Рис. 9. Зависимость от ц (K = 100 , m = 2 , без шума)

Таким образом, для восстановления изображений глазного дна без шума диапазон рабочих значений параметра µ составляет от 0,01 до 0,1 с соответствующим выбором количества итераций K в зависимости от требуемого распределения ВЧК.

Приведём результаты восстановления изображений глазного дна с аддитивным Гауссовым шумом порядка 1 %. В качестве исходных данных имеется стек наблюдаемых зашумлённых дефокусированных изображений, приведённых на рис. 10. Заметим, что в реальной ситуации «очищенное» от соседних слоёв изображение также содержит шумы измерения. Поэтому для контроля качества секционирования используется модифицированный ВЧК, при вычислении которого в моделируемой нами ситуации к искомому изображению в слое добавляется шум такой же природы и величины (но, возможно, другой реализации), что и в наблюдаемом дефокусированном изображении.

m = 1             m = 2             m = 3

Рис. 10. Стек дефокусированных изображений глазного дна с аддитивным Гауссовым шумом 1 %

В отличие от тестового объекта «Секторы», содержащего контрастные границы и участки однородного распределения интенсивности, в случае полутоновых изображений глазного дна с шумами для проявления тонких структур (сосуды) и волнистой топологии фона глазного дна, несущей важную офтальмологическую информацию о рецепторах, значение параметра µ =0,1 недостаточно для качественного восстановления, причём увеличение числа итераций лишь ухудшает картину. Улучшение качества восстановления наблюдается при уменьшении параметра до значения µ = 0,01. При этом метод успешно производит «секционирование» смешанных изображений, однако шум остаётся заметным, несмотря на существенное выравнивание векторного критерия (рис. 11).

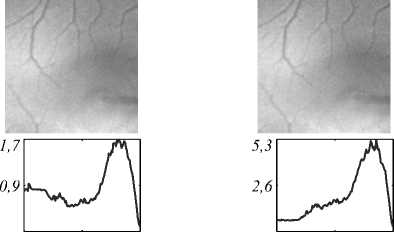
О 128   256               0     128   256

K = 10                     K = 40

Рис. 11. Секционирование изображений глазного дна ( µ = 0,01 , слой m =2 ) для Гауссова шума 1 %

Уменьшение значения параметра до µ = 0,001 (см. рис. 12) даёт наиболее адекватный результат как с точки зрения ВЧК, так и с точки зрения качественных особенностей восстановления. Для 100 итераций на среднем восстановленном изображении хорошо проявились как характерная фоновая текстура глазного дна, так и кровеносные сосуды.

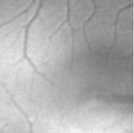
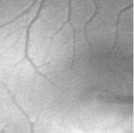
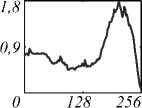
K = 100

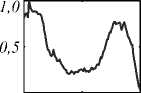
О 128   256

K =40

Рис. 12. Секционирование изображений глазного дна ( µ = 0,001 , слой m = 2 ) для Гауссова шума 1 %

Рассмотрим влияние пуассоновского шума около 2 % (100 000 фотонов на единицу интенсивности пикселя) на наблюдаемые изображения (см. рис. 13).

m =1            m =2            m =3

Рис. 13. Стек дефокусированных изображений глазного дна с пуассоновским шумом 2 %

Приведём результаты работы итерационного метода в зависимости от числа итераций при различных значениях параметра µ = 0,1, 0,01, 0,001.

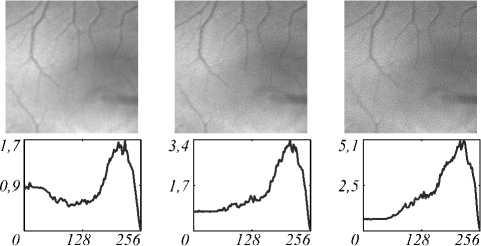
K = 2             K = 5             K = 10

Рис. 14. Секционирование изображений глазного дна ( µ = 0,1 , слой m = 2 ) для пуассоновского шума 2 %

Из рис. 14 видно, что для достижения приемлемой равномерности распределения векторного критерия при µ =0,1 на низких и средних частотах достаточно ограничиться небольшим количеством итераций (не более 10). Увеличение числа итераций приводит к росту искажений в высокочастотной области и соответствующей деградации изображения.

Анализ рис. 15 показывает, что при уменьшении параметра µ до значения 0,01, соответствующего предыдущему случаю, результата удаётся добиться ценой увеличения числа итераций до 20–40. При этом наблюдается равномерность векторного критерия в диапазоне низких и средних частот. Вместе с тем характерная фоновая текстура глазного дна всё ещё остаётся зашумлённой.

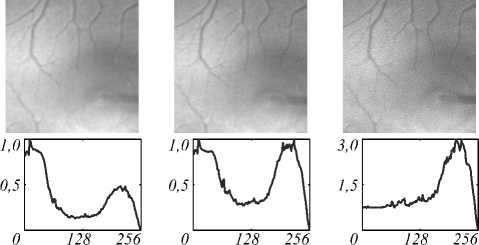
K = 5             K = 10            K = 40

Рис. 15. Секционирование стека изображений глазного дна

( µ = 0,01 , слой m = 2 ) для пуассоновского шума 2 %

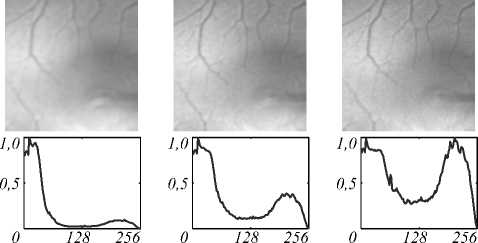
K = 10            K = 40            K = 100

Рис. 16. Секционирование изображений глазного дна (µ = 0,001, слой m = 2) для пуассоновского шума 2 % Уменьшением параметра µ до значения 0,001 с одновременным увеличением числа итераций до 100 (см. рис. 16) удаётся добиться хорошей равномерности векторного критерия вплоть до самых высоких частот с проявлением характерной фоновой текстуры глазного дна.

• 5.    О возможности распараллеливания метода

  Важной особенностью метода является возможность эффективного распараллеливания вычислительного алгоритма при использовании многоядерной структуры современных CPU и GPU. Об эффективности распараллеливания на многоядерных архитектурах в смысле сильной масштабируемости можно судить по графику ускорения программной реализации алгоритма в зависимости от числа используемых рабочих процессов в вычислительном пуле среды MATLAB (см. рис. 17). Расчёты проводились на персональном компьютере с процессором Intel Core i7-4790K, имеющем 4 процессорных ядра с поддержкой технологии Intel Hyper-Threading, для задачи с размерностью изображений 512×512. Как видно из графика, даже использование стандартных средств распараллеливания, имеющихся в среде MATLAB, позволяет сократить фактическое время расчёта в 4 раза.