Об одной задаче Коши

Рассматривается следующая задача Коши в Гильбертовом

пространстве Н dW)+^A (t ).d^=f (t),    (1) dtn     k=1 k       dtn -k dut)   = u(k)(0), k = 0,1,...,k -1,     (2) dt n                      ,             , ,   ,       , где u(t), f(t) - функции скалярного аргумента t € [O;T]

co значениями в   D(A) = I D(A (t)) о H, Ak (t) - вообще говоря , линейные неограниченные операторы , действующие в Н.

Предположим, что в задаче (1), (2) операторы     A ( t )

определены на постоянном всюду плотном множестве , замкнуты и сильно непрерывно дифференцируемы до порядка (п-к) включительно .

Пустъ L(X₁,X 2 ) - алгебра линейных ограниченных операторов, действующих из X 1 в X 2 ,   A ( ^m)(t) - сильная производная оператора

A k ( t )

порядка т и G = {U_h} - силъно непрерывная группа унитарных операторов в Н. По теореме Стоуна G обладает производящим оператором А , причем 1^-1А - самосопряженный оператор . Введем Гилъбертово пространство Н^е с нормой

II^He = ||(I - A2)2u|^ ,

I >  0.

Теорема . Пустъ операторы  A(m)(t) € L(H2,H) и инвариантны относительно группы G , т. е.

U_h A (^m) ( t ) = A ( ^m)( t ) U_h , h€(-^; от) ,     0 <  m <  n — k.

Тогда для решения задачи Коши уравнения ( 1 )

имеет место неравенство

||u|| < £||s-1u|| + ^(£)||Tu||, ¥s > 0

где

ф(г) = M

от

I n=0

( 16 M ² )

к ⁶  7

Nn

T = S + N ,

(Nu)(t) =

Jo1 |^ о ^(—i)"-™ 5^ (t — r )"-i'attu)s| «*

l

S = (I-A^) - .

Доказательство . Доказательство теоремы основывается на идея доказательство теоремы 3 работы [1].

К уравнению (1) применим n раз оператор обратного дифференцирования

u(t) +

(n-1)

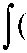
t - т ) n ¹ A ( t ) u ^{( n 1)}( r ) d ? + ... +

j ( t - т )^{n - 1} A ( t ) u ^{( n - 1)}( t ) d T

}

1 (n-1)!

t                          n-1 kk j (t - т) f(T )dT +1 —u(k) (0)

0                       k = 0 ^{k !}

В каждом интеграле последнего уравнения производные u(k)(t) перебросим на другие множители . Тогда получим

u(t) + (N 1 U)(t) = f 1 (t)

где tгм-1 m

(N1U)(t) = Jl^^(-1)k+m

0   m=0 k=0

c m

(n — к — 1)

IС

—

т)м k 1л1ттк)(т)]и(т)с/т,

t                          n-1 tk fi(t)  —— J(t-T"i;d 'XT?*k'(°)+

(n 1)! °                     k=0 k!

n - 1 n - l k

+XXX (-1) mcm l =1 k=1 m=1

, n + m - k - 1

-------------------A ^{( n - 1)} (°) u ^{( n - l - k )} (°). ( n + m - k - 1)!

Если к уравнению (3) применим оператор S, то получим

Su(t) + (Nu)(t) = f₂(t)

где f2(t) = Sf1(t)

Теперь проверим, что оператор S удовлетворят следующим условиям:

• 1)    S € L(H,H^l);    S A k mxt ) = A k ->( t ) S ;

• 2)    Оператор S как оператор H →H скалярен: (определение скалярного оператора см [1] ),

• 3.    KerS = 0 .

Так как

HSuHi = H^Hw

то S € L(H,H^l). Далее, в силу инвариантности A (^т) ( t ) относительно G,

A <^m) ( t )A = AA⁽_k^{m )} ( t ) и, таким образом, операторы      A ^m ( t )

коммутируют с S. Поэтому условие 1 выполняется. Оператор  1-1А самосопряжен, следовательно, оператор S эрмитов ( тем более скалярен) Итак, условие 2 тоже выполняется. Условие 3 следует из (5).

Кроме того, так как S € L(H, H^l), A k^m) ( t ) € L(H^l,H), то

SA <^m) ( t ) € L(H,H)

Таким образом, мы получили уравнение (4), которое удовлетворяет всем условиям теоремы 5 работы (1). Тем самым доказали утверждение теоремы.

Из доказанной теоремы и теоремы 6 работы (1) вытекает следующие.

Следствие. Если  (Su, u) > 0, ¥u€H , то имеет место оценка

||и|| < £||s-5ti|| + <р5(£)||Ти||, ¥е > 0 ,   б>0,

где та

Zn+1 е"ПП к=0