Об одной задаче нестационарного конвективного переноса с начальным распределением специального вида

Явления переноса встречаются в теплотехнике, электротехнике, магнитной гидродинамике, теории фильтрации, гидрогеологии и многих других областях технической практики. Среди этих явлений можно выделить явление гидродинамической дисперсии, включающее в себя несколько видов массопереноса нейтрального индикатора при фильтрации жидкостей. Основные из них: молекулярная диффузия, т.е. микроскопическое смешивание, механическая дисперсия, т.е. перемешивание, вызванное сложным строением среды и геометрией потока, адсорбция, т.е. сложный массоперенос из жидкости на поверхности твердой фазы и некоторые другие.

Для математического описания явления гидродинамической дисперсии было предложено [1, 2] уравнение, которое в общей криволинейной системе координат может быть представлено в виде

ЭС .

— = di^DgradC - Си] (1)

∂ t

В этом уравнении С - относительная концентрация переносимого фильтраци онным потоком вещества, U^ - скорость потока, D - коэффициент гидродинамической дисперсии, который зависит от скорости течения и в общем случае является тензором второго ранга.

Из уравнения (1) могут быть получены различные его частные случаи [3, 7], учитывающие размерность модели переноса, стационарность или нестационарность процесса, а также вклад отдельных видов массопереноса в общий процесс дисперсии. Однако, число задач, решения которых получено в замкнутом виде ограничено из-за трудностей возникающих при по- лучении общих решений соответствующих дифференциальных уравнений.

Имеющиеся экспериментальные исследования [4, 5] указывают на то, что в зависимости от значений критериальных чисел Пекле и Рейнольдса диапазон изменения скоростей течения можно разбить на несколько интервалов, в пределах которых доминируют отдельные виды массопере-носа. В областях, где скорости течения значительные преобладает конвективный перенос, в уравнении (1) можно пренебречь производными второго порядка по координатами, и, тогда в цилиндрической системе координат для одномерного случая оно примет вид

1 д ( rvC )     д C  дN

---+ п₀— = — ,  (2)

r    ∂r        ∂t    ∂t здесь n - пористость среды, N- концентрация вещества в твердой фазе.

Если предположить, что фильтрационное течение создается логарифмическим источником (стоком), т.е., и = + — Q 0 —,

2nBn0r где Q0 – объемный расход жидкости, например дебет совершенной скважины, B – линейный размер источника (стока) или мощность фильтрационного пласта, то уравнение (2) для случая сходящегося течения при отсутствии адсорбции (N=cоnst) примет вид:

1 д (с)  п0 ас r ⋅ ∂r + Q ∂t

Q =  Q0.

2пВп0

Следуя общей теории решения дифференциальных уравнений в частных производных первого порядка [6], составим характеристическую систему уравнений

QdtC r∂r== по

Характеристики (интегралы) системы C 1 =C и уравнения (3) можно представить в виде

,  2Q _  _ r2 —— t = C2. Тогда общее решение no

C(r,t) = Ф(у),  у = r2 -2Qt ,(5), no где  Ф(у) - некоторая дифференцируе мая функция переменных ( r, t).

Для дифференциальных уравнений вида (3) возможна постановка задачи Коши [6], т.е. задание начальных условий вида C(0, t) = ^(r). (6).

Учитывая вид общего решения уравнения (3) зададим начальное распределение выражением

^(0, r ) = Ar ^a e - ^e r , (7).

Тогда решение поставленной задачи Коши с указанным начальным распределением будет иметь вид a        1

C ( r,t ) = A -у ■ e" ^{ву 2}   .   (8)

В этом выражении A, α и β – некоторые коэффициенты, причем А нормировочный коэффициент, а за счет произвольности коэффициентов α и β начальному распределению (7) можно придать требуемую форму.

Для иллюстрации сказанного удобно ввести безразмерные переменные [7] ρ = ^r – безразмерные координаты, a

τ = Q t – безразмерное время, a – некото-a рый характерный линейный размер, например продольная дисперсион-ность [5].

В этих переменных постановка и решение задачи (3), (7), (8) могут быть представлены в следующем виде dC дт

--^ C , т >  0 , р> 0, р ^дР

C (0, р ) = Ар ^а е ^{- вр}        ,                     (10)

C ( р , т ) = A^(2 т + р ²) ^а * e" ^в^ .           (11)

Исследование выражения (11) показывает, что максимум функции C ( р,т) в зависимо

( ^а )² - 2т ,   (12)

сти от т находится в точке с координатой р а.

максимальное значение функции (11) определяется по формуле C_maх = А (—) ^а * e ^а , т. е.

остается постоянным до момента т = — ( ^а )²,   (13), а скорость перемещения максимума

- в

(7) и = ( ^а )² - 2 т

—

Рисунок 1 иллюстрирует динамику распределения концентрации с течением безразмерного времени т .

Графики зависимости концентрации C ( р,т) построены при следующих значениях параметров: а = 12 ; в = 6; A = ( e )¹². Нормировочный коэффициент А выбран так, чтобы максимум концентрации начального распределения был равен 1.

Таким образом, для рассмотренного примера

C ( р , т ) =

1(2 т + р ²) * e^г" ^{- T+Pp^}

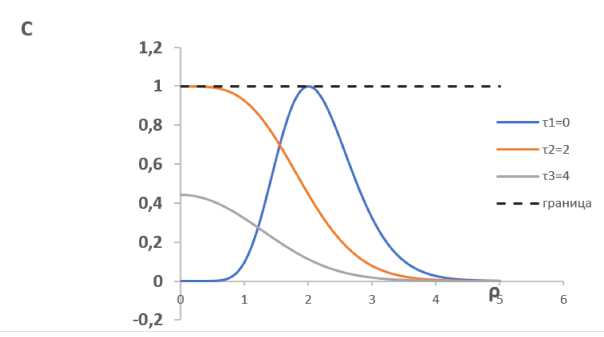
Рис. 1. Кривые распределения концентрации для различных моментов приведенного времени

Аналогичным образом можно получить решение задачи Коши уравнения (2) для некоторых моделей учитывающих раство-      Например, в случае равновесной ад- рение веществ, выпадение в осадок и кри- сорбции [4] сталлизацию.

∂ N ∂ C

---= n ₀ • Г — , ∂ t ∂ t

Г - параметр изотермы массообмена Генри. В этом случае уравнение (2) приобретает вид

τ

• ^{d ( ruC} ) + n (1 - Г ) d C = 0 d r       ⁰         dt

Решение задачи Коши для уравнения (17) аналогично приведенному выше и имеет вид (15). В этом случае достаточно

I ^τ заменить переменные τ на τ =      .

Полученные решения могут быть исполь- зующих процесс массопереноса. Для этого необходимо создать соответствующее начальное распределение индикатора, зарегистрировать его на стоке фильтрационного течения и произвести замеры концентрации в различные моменты времени.

зованы для оценки параметров, характери-