Об одном алгоритме классификации с использованием коллективов непараметрических моделей

В современных теории и практике компьютерного анализа данных классификация занимает важное место. В настоящее время существует множество подходов к решению задачи классификации в случае, когда исследователю доступна случайная выборка измерений классифиционных признаков с указаниями учителя [1; 2]. Многие из этих подходов основаны на использовании байесовой процедуры принятия решения, когда решающее правило можно формировать в классе непараметрических регрессионных моделей. Однако высокая вычислительная сложность при реализации соответствующих алгоритмов затрудняет использование указанного подхода для случаев, когда размерность вектора признаков и объем обучающей выборки достаточно велики. Авторами предложен алгоритм классификации с использованием метода k ближайших соседей, предполагающий декомпозицию задачи с использованием коллективов решающих правил и упорядочиванием выборки.

Рассмотрим алгоритм построения непараметрического классификатора на примере двуальтернативной задачи распознавания образов.

Пусть ( x i , y i ) , i = 1, n - обучающая выборка, где x i = ( x d , d = 1, D ) , i = 1, n - значения признаков классифицируемых объектов (среди признаков есть как непрерывные, так и дискретные); y i – указания учителя об их принадлежности к одному из двух классов:

[ 1, X i ^e^,

У - = 1

[- 1, x - eQ 2 ;

( x i , y i ) , i = 1, m - экзаменующая выборка. Условные плотности вероятности распределения значений признаков x для обоих классов неизвестны.

Решающее правило имеет вид

[ x- eQ 1 , f ( x - ) > C ,

[xleO1, f(xi )< C, где C - порог отсечения, C e [-1, 1]; fx) - решающая функция, f (x) e [-1, 1]. В качестве оценки решающей функции fˆ (x) будем использовать непараметрическую статистику [3]:

^{f ( x} ) =

nD

Z у- П ф i = 1 d = 1

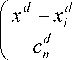
nD

ЕП ф i = 1 d = 1

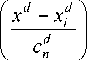
где Ф – ядерная функция; c n – параметры размытости, удовлетворяющие следующим свойствам: c_n >  0; lim c n = 0; lim n ( c n ) D = да .

n ^да          n ^да

Введем следующие обозначения:

– TP ( C ) – верно классифицированные положительные примеры, принадлежащие первому классу;

– TN ( C ) – верно классифицированные отрицательные примеры, принадлежащие второму классу;

– FN ( C ) – положительные примеры, классифицированные как отрицательные (ошибка I рода);

– FP ( C ) – отрицательные примеры, классифицированные как положительные (ошибка II рода);

– TPR ( C ) – доля истинно положительных примеров: TPR ( C ) =---- ^{TP (} C ⁾----;

TP ( C ) + FN ( C )

– FPR ( C ) – доля ложно положительных примеров:

FPR ( C ) =--- FP ( C )---.

TN ( C ) + FP ( C )

Зависимость TPR ( C ) от FPR ( C ) образуют кривую ROC (рис. 1).

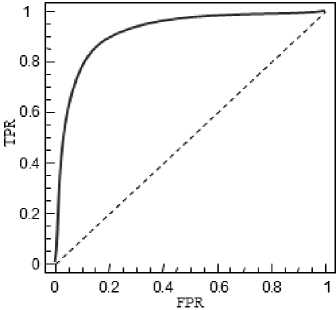
Рис. 1. Кривая ROC

Оптимизация по параметрам размытости c n происходит в режиме holdout [4] из условия максимума AUC – площади под кривой ROC [5].

Построение решающей функции (1) для неусеченного ядра Ф во всех точках экзаменующей выборки потребует O ( nm ) вычислительных операций. При использовании усеченных ядер время вычисления сокращается, так как локальное усреднение производится только в окрестности каждой точки экзаменующей выборки.

Однако если учесть, что для оптимизации параметров размытости c n необходимо повторять процедуру оценивания решающей функции (1) несколько раз, то применение этой функции для выборок большого объема потребует значительного количества вычислительных ресурсов [6]. Сократить количество вычислительных операций для построения оценки регрессии возможно за счет применения линейных непараметрических коллективов решающих правил, смысл которых состоит в декомпозиции исходной задачи, построении семейства локальных решающих функций и последующей их организации в едином линейном решающем правиле [1].

Для построения локальных (частных) решающих функций предлагается формировать наборы признаков x ( j ) , j = 1, N из исходных x = ( x 1 , x 2 ,,,,, x^D ) , причем каждый набор признаков x( j) должен содер жать только один непрерывный признак и произволь ное число дискретных . Семейство частных решающих функций f j ( x ( j )) ( j = 1, N ) строится на основании

модель, оптимизация критерия AUC производится по одному параметру – числу ближайших соседей k .

Предлагаемый алгоритм работает следующим образом (рис. 2). Для построения оценки в точке i 1 достаточно ближайших соседей, для которых значения признака x l ^{- 1} равны 1, Объем подвыборки, значения признака x l ^{- 1} элементов которой равны 3, меньше 2 к , и при построении оценки в точке i 2 происходит включение в оценку элементов соседней подвыборки.

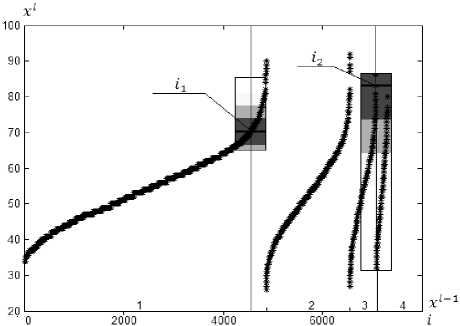
Рис. 2. Работа алгоритма коллективной оценки k ближайших соседей для упорядоченной выборки

обучающих выборок V j = ( x i ( j ), y, , i = 1, n ), j = 1, N ,

Процедуру построения частной модели можно условно разбить на два этапа: упорядочивание выборки V j и оценку k ближайших соседей.

Зададим процедуру упорядочивания выборки.

Пусть сформирован набор признаков

x ( j ) = ( x 1 , x 2 ,

..

,, x l ) , где x 1 , x ²,,,,, x^{1 1} - дискретные

Для построения одной частной решающей функции во всех точках экзаменующей выборки требуется O ( km ) вычислительных операций.

Интеграция частных решающих функций f j ( x ( j )) ( j = 1, N ) в линейном коллективе решающих правил f ˆ( x ) [1] осуществляется в соответствии с процедурой

N

f( x) = Е wjfi(x (j)), j=1

признаки; x l – непрерывный признак, l <  D . На первом шаге производится упорядочивание выборки V j по x 1 , далее – упорядочивание подвыборок с одина- 12

ковыми значениями признаков x по x и так до непрерывного признака x l включительно.

К упорядоченному массиву наблюдений можно применить оценку k ближайших соседей:

где W j ( j = 1, N ) - положительные веса, для которых справедливо равенство

N

Е w j = 1,

j = 1

v + к

Еф

xi

^^^^^^»

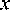
f x¹ ) =

i = v - к

i * v

c

x n

yi

где v – индекс точки экзаменующей выборки в упорядоченной выборке V j ; c nx – максимальное расстояние от x¹ до x i ¹ такое, что | i - v | <  к , Таким образом, не-

зависимо от числа признаков, включенных в частную

В силу того что веса w j оптимизируются после построения ча стных решающих функций f j ( x ( j )) ( j = 1, N ), перестроения моделей с целью оптимизации не требуется.

Таким образом, сокращение количества вычислительных операций достигается как за счет сокращения количества одновременно настраиваемых параметров, так и за счет экономии вычислительных ресурсов при построении решающих функций.

Численные исследования алгоритма проводились на данных Give Me Some Credit [7], содержащих информацию о кредитной истории 150 000 клиентов банка. Требовалось синтезировать решающее правило, позволяющее отнести клиента к одному из двух классов: заемщикам с наличием или отсутствием

выплат, просроченных на срок более 90 дней за 2 следующих года.

Непрерывные признаки: x 1 – общий баланс по кредитным картам, деленный на сумму кредитного лимита; x 2 – возраст заемщика; x 3 – ежемесячные выплаты долгов, алиментов, расходы на проживание, деленные на ежемесячный доход; x 4 – ежемесячный доход.

Дискретные признаки: x 5 – количество просроченных выплат на срок от 30 до 59 дней за 2 предыдущих года (7 различных значений для 99,756 % наблюдений, 0,179 % наблюдений – пропуски данных); x 6 – количество открытых кредитов (кредиты на покупку автомобиля и ипотека) и кредитных карт (27 значений для 99,4 % наблюдений); x 7 – количество просроченных выплат на срок более 90 дней за 2 предыдущих года (7 значений для 99,752 % наблюдений, 0,179 % наблюдений – пропуски данных); x 8 – количество ипотечных займов (8 значений для 99,799 % наблюдений); x 9 – количество просроченных выплат на срок от 60 до 89 дней за 2 предыдущих года; x 10 – число иждивенцев (8 значений для 97,36 % наблюдений, 2,616 % наблюдений – пропуски данных).

По признакам x 5 , x 6 , x 7 , x 8 , x 9 , x 10 можно производить последовательные сортировки, а по переменным x 1 , x 2 , x 3 , x 4 – вычислять оценку k ближайших соседей. В качестве ядерной функции выбрано треугольное ядро [6].

Наборы признаков формировались последовательным добавлением дискретных признаков x 5 , x 6 , x 7 , x 8 , x 9 , x 10 к непрерывным признакам x 1 , x 2 , x 3 , x 4 . Значения AUC для частных решающих функций (2), построенных по выборкам V j со всевозможными наборами из одного и двух признаков, приведены в табл. 1, с наборами из двух и трех признаков – в табл. 2.

Учет признака x 6 при построении частной решающей функции по непрерывному признаку x 1 и признака x 10 при построении частной решающей функции по непрерывному признаку x 2 привел к уменьшению критерия качества (см. значения, выделенные курсивом в табл. 1).

В результате была получена убывающая по AUC последовательность наборов признаков. Наибольшему значению AUC соответствует набор признаков ( x 7 , x ⁹, x ⁵, x ⁸, x ¹), AUC = 0,851 9.

Таблица 1

Значения AUC для частных моделей, построенных с использованием одного или двух признаков

x 1	0,782 8	0,819 7	0,779 0	0,818 1	0,785 2	0,810 2	0,786 5
x 2	0,633 2	0,754 0	0,652 4	0,733 5	0,651 1	0,713 1	0,632 9
x 3	0,578 6	0,723 0	0,638 7	0,715 1	0,641 6	0,677 4	0,587 1
x 4	0,580 4	0,723 1	0,605 8	0,695 4	0,605 4	0,672 0	0,595 1
Признак	–	x 5	x 6	x 7	x 8	x 9	x 10

Таблица 2

Значения AUC для частных моделей, построенных с использованием двух или трех признаков

x 1	0,819 7	0,816 5	0,841 6	0,827 2	0,836 9	0,821 4
x 2	0,754 0	0,769 7	0,798 3	0,761 3	0,779 7	0,753 0
x 3	0,723 0	0,759 6	0,786 1	0,752 5	0,760 6	0,726 6
x 4	0,723 1	0,747 7	0,774 4	0,739 6	0,755 8	0,730 3
Признак	x 5	x 5 x 6	x 5 x 7	x 5 x 8	x 5 x 9	x 5 x 10
x 1	0,816 6	0,779 0	0,817 3	0,784 5	0,809 6	0,775 4
x 2	0,764 7	0,652 4	0,737 3	0,656 7	0,719 4	0,646 8
x 3	0,751 8	0,638 7	0,725 8	0,660 7	0,707 1	0,632 6
x 4	0,741 5	0,605 8	0,705 2	0,610 8	0,688 6	0,615 3
Признак	x 6 x 5	x 6	x 6 x 7	x 6 x 8	x 6 x 9	x 6 x 10
x 1	0,842 1	0,820 1	0,818 1	0,822 2	0,834 6	0,816 9
x 2	0,797 1	0,744 5	0,733 5	0,741 8	0,766 5	0,733 4
x 3	0,784 1	0,736 6	0,715 1	0,745 7	0,752 8	0,718 4
x 4	0,777 0	0,713 5	0,695 4	0,7144	0,7377	0,705 6
Признак	x 7 x 5	x 7 x 6	x 7	x 7 x 8	x 7 x 9	x 7 x 10
x 1	0,821 3	0,775 2	0,823 2	0,785 2	0,815 6	0,788 2
x 2	0,759 8	0,657 9	0,740 5	0,651 1	0,723 3	0,651 9
x 3	0,750 3	0,662 4	0,743 1	0,641 6	0,716 9	0,647 6
x 4	0,738 5	0,611 2	0,711 4	0,605 4	0,690 2	0,617 1
Признак	x 8 x 5	x 8 x 6	x 8 x 7	x 8	x 8 x 9	x 8 x 10

Окончание табл. 2

x 1	0,832 2	0,807 3	0,831 7	0,813 3	0,810 2	0,808 0
x 2	0,779 8	0,727 9	0,766 4	0,724 3	0,713 1	0,712 6
x 3	0,760 9	0,716 6	0,753 7	0,719 4	0,677 4	0,680 7
x 4	0,756 0	0,694 4	0,732 4	0,694 2	0,672 0	0,684 6
Признак	x 9 x 5	x 9 x 6	x 9 x 7	x 9 x 8	x 9	x 9 x 10
x 1	0,816 2	0,770 0	0,815 5	0,780 4	0,806 6	0,786 5
x 2	0,751 8	0,646 8	0,731 6	0,651 0	0,711 9	0,632 9
x 3	0,725 6	0,631 0	0,713 9	0,646 8	0,680 6	0,585 7
x 4	0,728 5	0,615 3	0,703 4	0,617 0	0,682 5	0,585 1
Признак	x 10 x 5	x 10 x 6	x 10 x 7	x 10 x 8	x 10 x 9	x 10

На основе анализа результатов построения частных моделей с различными наборами признаков были сделаны выводы о степени влияния каждого признака на отклик относительно других, т. е. было проведено ранжирование непрерывных и дискретных признаков:

x > x > x > x , x5 ® x7 ® x9 > x8 > x6 > x 10, где a > b означает, что влияние признака a выше влияния признака b; a ≈ b – однозначное сравнение влияния не может быть произведено.

Объединение частных моделей в линейный коллектив позволяет повысить качество модели: при объединении 5 частных моделей AUC = 0,861 1, при объединении 13 частных моделей AUC = 0,864 1, дальнейшее же увеличение коллектива к существенному увеличению AUC не приводит. Объединение проводилось последовательным добавлением случайно выбранной частной модели к коллективу. В случае отсутствия улучшения качества модели добавленная частная модель удалялась. За первоначальный коллектив была взята частная модель, построенная по набору признаков ( x 7 , x 9 , x 5 , x 8 , x 1 ) и оптимальная в смысле AUC. Для решения задачи выбора оптимального набора признаков потребовалось построить 42 частные модели: 4 – для выбора непрерывного признака, 6 – для выбора первого дискретного признака, 5 – для выбора второго дискретного признака, 4 – для выбора третьего дискретного признака, 3 – для выбора четвертого дискретного признака и 24 = 4! для определения порядка дискретных признаков.

Предлагаемый алгоритм сравнивался с алгоритмами, вычислительные затраты которых также линейно зависят от объема выборки и количества элементов в коллективе:

– бинарное дерево регрессии [2] (89 вершин) – AUC = 0,852 4;

– алгоритм Random Forest [8] (500 деревьев) – AUC = 0,864 2.

При равных показателях критерия AUC предлагаемый алгоритм требует меньшее количество вычислительных ресурсов.