Об одном численном алгоритме решения интегральных уравнений первого рода в пространствах L2, основанном на обобщенном принципе невязки
Автор: Сидикова Анна Ивановна, Ершова Анна Александровна
Рубрика: Моделирование и компьютерные технологии
Статья в выпуске: 2 т.15, 2015 года.
Бесплатный доступ
Рассматривается одномерное интегральное уравнение Фредгольма I рода с замкнутым ядром, имеющим решение в классе W 12[ a,b] с однородным граничным условием первого рода в точке a. Задача сводится к новому интегральному уравнению относительно производной искомого решения. Полученное интегрального уравнение подвергается конечномерной аппроксимации специального вида, которая позволяет при использовании вариационного метода регуляризации А.Н. Тихонова с выбором параметра регуляризации по обобщенному принципу невязки свести задачу к специальной системе линейных алгебраических уравнений. Проводится также априорная оценка точности полученного устойчивого конечномерного приближенного решения, учитывающая точность конечномерной аппроксимации задачи. Использование данного подхода приводится на примере задачи определения фононного спектра по его теплоемкости, зависящей от температуры, которая, как известно, сводится к интегральному уравнению первого рода.
Регуляризация, интегральное уравнение, оценка погрешности, некорректная задача
Короткий адрес: https://sciup.org/147155040
IDR: 147155040 | DOI: 10.14529/ctcr150207
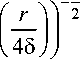
Список литературы Об одном численном алгоритме решения интегральных уравнений первого рода в пространствах L2, основанном на обобщенном принципе невязки
- Гончарский, А.В. Конечноразностная аппроксимация линейных некорректных задач/А.В. Гончарский, А.С. Леонов, А.Г. Ягола//Журн. вычисл. матем. и матем. физики. -1974. -Т. 14, № 1. -С. 15-24.
- Танана, В.П. Об оценке погрешности регуляризующего алгоритма, основанного на обобщенном принципе невязки, при решении интегральных уравнений/В.П. Танана, А.И. Сидикова//Вычислит. методы и программирование. -2015. -Т. 16, № 1. -C. 1-9.
- Танана, В.П. Проекционные методы и конечноразностная аппроксимация линейных некорректных задач/В.П. Танана//Сиб. мат. жур. -1975. -Т. 16, № 6. -С. 1301-1307.
- Васин, В.В. Дискретная сходимость и конечномерная аппроксимация регуляризующих алгоритмов/В.В. Васин//Журн. вычисл. матем. и матем. физики. -1979. -Т. 19, № 1. -C. 11-21.
- Данилин, А.Р. Об условии сходимости конечномерных аппроксимаций метода невязки/А.Р. Данилин//Изв. вузов матем. -1980. -№ 11. -С. 38-40.
- Леонов, А.С. О связи метода обобщенной невязки и обобщенного принцпа невязки для нелинейных задач/А.С. Леонов//Журн. вычисл. матем. и матем. физики. -1982. -Т. 22, № 4. -C. 783-790.
- Данилин, А.Р. Об оптимальных по порядку оценках конечномерных аппроксимаций решений некорректных задач/А.Р. Данилин//Журн. вычисл. матем. и матем. физики. -1982. -Т. 22, № 4. -C. 1123-1129.
- Танана, В.П. Об одном проекционно-итеративном алгоритме для операторных уравнений первого рода с возмущенным оператором/В.П. Танана//Доклады Академии наук. -1975. -Т. 224, № 5. -С. 1028-1029.
- Тихонов, А.Н. О решении некорректно поставленных задач и методе регуляризации/А.Н. Тихонов//Доклады Академии наук. -1963. -Т. 151, № 3. -С. 501-504.
- Гончарский, А.В. Обобщенный принцип невязки/А.В. Гончарский, А.С. Леонов, А.Г. Ягола//Журн. вычисл. матем. и матем. физики. -1973. -Т. 13, № 2. -С. 294-302.
- Танана, В.П. Методы решения операторных уравнений/В.П. Танана. -М.: Наука, 1981. -С. 156.
- Танана, В.П. Оценка погрешности метода регуляризации А.Н. Тихонова при решении одной обратной задачи физики твердого тела/В.П. Танана, А.А. Ерыгина//Сиб. журн. индустр. математики. -2014. -№ 2. -С. 125-136.
