Об одном классе электростатических полей с пространственно-временнoй фокусировкой (1989 г.)

В статье определен новый (на тот момент — 1989 г.) класс электростатических полей, в котором осуществляется пространственно-временнáя фокусировка в направлении разделения ионов по времени пролета, проанализированы его свойства. Описывается общий подход к синтезу потенциалов с идеальной про-странственно-временнóй фокусировкой, впоследствии с успехом использованный Ю.К. Голиковым при синтезе конкретных конфигураций для многооборотных времяпролетных масс-анализаторов. Поле, рассмотренное в данной работе в качестве основного примера, получило широкую известность в силу использования его впоследствии в новом классе масс-спектрометрических приборов — электростатических ловушках "Орбитрап"™ с Фурье-анализом.

Кл. сл. : пространственно-временная фокусировка, времяпролетные масс-анализаторы, гиперболический потенциал, логарифмически-гиперболический потенциал, гармонические осцилляции в электрическом поле

ПРЕДИСЛОВИЕ

Эта статья была опубликована впервые в сборнике научных трудов "Научное приборостроение. Электронно- и ионная оптика" (Л.: Ленинградское отделение изд-ва "Наука", 1989; отв. редактор М.Л. Александров; с. 3–7). По-видимому, исторически эта работа является первой научной публикацией, в которой рассматриваются вре-мяпролетные свойства осесимметричного лога-рифмически-гиперболического потенциала

U ( r , z ) = U о ( k log r + z ² - r ²/2 ) (1)

(для других приложений само это поле (1), скорее всего, впервые появилось в работе [1]). Дальнейшим развитием данной тематики послужили работы [2–6], патенты [7]*) и монография [8] (патент [9] и публикация [10] эквивалентны [6] — к сожалению, без ссылки на первоисточник). Конечно же, необходимо отметить выдающееся достижение А.А. Макарова и его команды — создание на основе эффекта идеально-гармонических осцилляций ионов в поле (1) принципиально нового класса масс-спектрометрических приборов — электростатических ловушек "Орбитрап"™ с Фурье-анализом [11–17].

При подготовке работы к повторной печати были исправлены отдельные опечатки и неточности и внесены некоторые добавления, основанные на устных уточнениях Ю.К. Голикова, высказанных в частных беседах. Кроме того, в качестве приложения добавлен текст авторского свидетельства № 1247973 (СССР) "Времяпролетный масс-спектрометр" и ссылки на последующие работы Ю.К. Голикова и его учеников в этом направлении.

О СТРУКТУРЕ ЭЛЕКТРОСТАТИЧЕСКИХ ПОЛЕЙ С НУЖНЫМИ СВОЙСТВАМИ

За последние годы в связи с развитием импульсных методов ионизации вырос интерес к времяпро-летным масс-спектрометрам (ВПМС), позволяющим получить полный спектр масс для каждого события ионизации. Однако, как и прежде, основными факторами, ограничивающими широкое применение ВПМС, являются сравнительно низкие значения разрешающей способности и чувствительности.

Основной вклад в "размытие" ионного пакета при прохождении аналитической части прибора вносят пространственный и энергетический разбросы ионов в начальный момент времени. Наиболее удачными на сегодняшний день с точки зрения компенсации влияния энергетического разброса ионов на разрешающую способность явля- ются приборы типа масс-рефлектрон, в которых роль компенсирующего элемента выполняет плоское электростатическое зеркало [18]. Задача дальнейшего повышения разрешающей способности ВПМС наиболее конструктивно может быть решена за счет использования электростатических полей, обеспечивающих более сильную простран-ственно-временнýю фокусировку ионного пакета, и в том числе таких, время пролета в которых не зависит от начальных условий движения ионов.

Какова же структура полей, обладающих свойством независимости времени пролета от начальных параметров движения? Легко обнаружить, что в случае прямолинейного движения этим уникальным свойством обладает линейный осциллятор, потенциал которого имеет вид и = - 22, (2)

где k — коэффициент восстановления. Движение частицы с массой m в этом случае носит колебательный характер и описывается уравнением

2 (t ) = 20COS tot + —Sin tot , (3) ω где 20, 20 — соответственно положение и скорость частицы в начальный момент времени, to = ^k/m — частота колебаний частицы. Из уравнения (3) непосредственно следует, что период колебаний T, определяемый как T = 2п^m/k , является функцией массы частицы и коэффициента k , являющегося характеристикой осциллятора, и не зависит от 20, 20.

Возвращаясь к рассмотрению движения заряженных частиц в электростатических полях, определим структуры полей, движение в которых вдоль заданного направления, например вдоль оси OZ , подобно линейному осциллятору.

Для организации такого движения естественно потребовать, чтобы потенциал электростатического поля Φz вдоль оси OZ был аналогичен потенциалу линейного осциллятора (2) и, следовательно, имел вид ф = -22 = фа I I , (4) 2 2 0 (1)

где a — некоторая безразмерная константа; Φ ₀ и l — характерный потенциал поля и характерный линейный размер поля соответственно (размерные величины).

Потенциал в пространстве X , Y , Z с учетом равенства (4) должен иметь вид

Ф ( X , Y , Z ) = Ф о

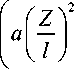
+ p I X , Y 1 11

В силу того, что потенциал Ф(X, Y, Z) должен ж рI X Y i быть гармоничным, функция PI ~,у удовлетворять уравнению Пуассона вида должна

A P | X , Y I 11

- 2 а .

Движение частиц в полях с потенциалом (5) вдоль оси OZ носит колебательный характер и происходит согласно уравнению (3) с частотой колебаний to = 1 "’^2 qФ₀ а/m и периодом Т₂ = 2п1 ^ 2 qФ₀а .

Таким образом, все частицы, вылетевшие из плоскости Z = -Z0 в виде бесконечно плоского пакета, соберутся в плоскости Z = + Z0 в моменты времени

t = 2^+1 т t1 n /^ T2

и в плоскости

7 --7

= ₀

в моменты времени 12n = nT2 (n = 0^да). Следует подчеркнуть, что период колебаний Tz и, следова- тельно, времена пролета частицы t 1n и t2n до плоскостей Z = -Z0, Z = + Z0 не зависят от начальных условий движения (положения и скорости) и являются лишь функцией параметров поля (характерных значений потенциала Φ0 и линейного размера l ) и параметров самой заряженной частицы (массы и заряда). Таким образом, вдоль направления дисперсии по времени пролета (вдоль оси OZ ) осуществляется идеальная пространст-венно-временнáя фокусировка.

Движение вдоль плоскости XY целиком определяется видом функции P ( x , у ) в (5), которую можно рассматривать как сумму функций

P ( x , у ) = pi ( x , у ) + p 2 ( x , у ) ,       (7)

полагая, что функции p ₁ и p ₂ удовлетворяют условиям

A p1 = - 2 а , A p ₂ = 0.                (8)

Здесь и далее используются безразмерные величины x = X/1 , у = Y/1 , 2 = Z/1 .

В декартовой системе координат функцию p ₁ удобно взять в виде p 1 = bx ² + су ², при этом параметры b и c в силу условий (8) удовлетворяют равенству b + с = - а . Функция p ₂ в равенстве (7) является произвольной двухмерной гармонической функцией.

Класс функций P , удовлетворяющих условию (7), (8), достаточно широк. Богат возможностями уже самый простой случай, когда p ₂ ( x , y ) = 0. В этом случае потенциал имеет вид

Ф( x, y, z ) = Ф0 (az2 + bx2 + cy2), a + b + c = 0, и эквипотенциали поля представляют собой гиперболоиды. При этом возможны следующие варианты.

• 1)    c >  0, тогда b = - ( a + c ) <  0 . Ион колеблется с периодами T_y = 2nJ ( Sjc ) и T_z = 2^ ( S^ ) вдоль осей OY и OZ соответственно (здесь S = l-'^2q Ф 0/ m ).

Периоды Ty и Tz равны, если a = c ( b = - 2 a ).

В этом случае поле является осесимметричным с распределением потенциала

Ф(x,y,z) = Фо (r2 -2x2), r2 = z2 + y2, и эквипотенциали поля представляют собой гиперболоиды вращения. Легко заметить, что при этих условиях в плоскости достигается идеальная пространственно-временнáя фокусировка точки в точку без дисперсии по энергии. Такой вариант фокусировки применительно к энергоанализу изучался в работе [19]. Однако для движения вдоль оси OX траектории экспоненциально расходятся при малейшем возмущении начальных условий в этом направлении.

• 2)    c <  0, b <  0. Характер движения совсем иной. Колебания иона происходят лишь вдоль оси OZ . Траектории экспоненциально расходятся во времени как при возмущении начальных параметров движения вдоль оси OX , так и при возмущении начальных параметров движения вдоль оси OY , если только начальные координаты и скорости не связаны жесткой зависимостью. При этом возможен вариант осевой симметрии поля (при 1

• b = c = -— a ), потенциал которого имеет вид

Ф ( x , y , z ) = Ф ₀ a ( z ² - r ² ) , r ² = x ² + y ².

Многообразие полей можно существенно расширить, если p 2 ^ 0. При этом вид функции p 2 ( x , y ) полностью определяет характер движения в плоскости XY и свойства пространственно-временнóй фокусировки в ней.

Интересным с точки зрения реализации является вариант осесимметричного поля так называемого квазиконического типа [20], для которого p 2 ( x , y ) = k In r ( r ² = x ² + y 2 ) и потенциал имеет вид

^Ф ( ^x , y , ^z ) = ^ф о

az

V

-

ar ²

--+ k In r + const

(это единственный осесимметричный потенциал вида (5)).

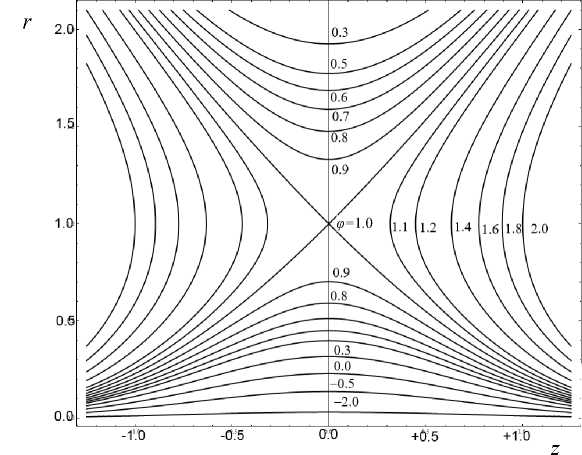
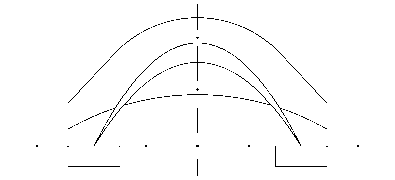
Ф ( z , r ) = z ² - r ²/2 + In r + 3/2

Рис. 1. Форма эквипотенциалей поля

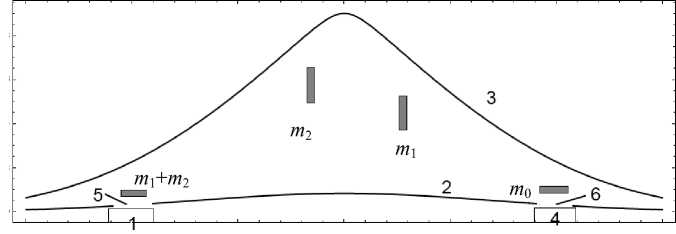
Рис. 2. Схема времяпролетного масс-спектрометра с идеальной про-странственно-временнóй фокусировкой

Исследование изменения формулы (9) при масштабировании переменных z , r , Φ ₀ показывает, что существует только три принципиально разных варианта: a = 1, k = 1; a = 1, k = - 1; a = 1, k = 0 . Все остальные получаются из этих базовых типов за счет масштабирования координат z , r , выбора потенциального множителя Φ ₀ и пересчета константы const . Из них лишь вариант a = 1, k = 1 ( Ф₀ >  0, a >  0, k >  0) представляет интерес с точки зрения ограниченности движения в радиальном направлении и наличия циклических осцилляций вдоль оси OZ . Эквипотенциали поля (9) приведены на рис. 1 при значениях Ф ₀ = 1, k = a = 1, const = 3/2 в плоскости ZR . Эквипотенциальные поверхности представляют собой поверхности вращения с плоскостью симметрии z = 0. При a >  0, k >  0 поле делится эквипотенциальными поверхностями, проходящими через седловую точку z = 0, r = ^k/a , на четыре характерные по конфигурации области, из которых наиболее компактной и удобной для дальнейшей реализации является область 1. В этой области, непосредственно примыкающей к оси вращения OZ , эквипотенциали представляют собой квазиконусы, соединенные у основания в плоскости симметрии z = 0.

Следует отметить, что форма эквипотенциальной поверхности, выходящей из фиксированной геометрической точки на плоскости симметрии z = 0, существенно зависит от отношения параметров k и a . Так, при увеличении отношения k a эквипотенциали в области 1 с фиксированной точкой старта "выпрямляются", образуя почти цилиндрические поверхности со слабой деформацией, постепенно приближаясь к геометрии поля заряженной нити. Аналогичная ситуация возникает и при переходе к рассмотрению эквипотенциалей с более низкими значениями уровней, т. е. при рассмотрении эквипотенциалей, находящихся ближе к оси OZ . При уменьшении же отношения k a (или же при приближении стартовой точки эквипотенциали к седловой точке) эквипотенциальные поверхности в области 1 по форме приближаются к гиперболоидам.

АППАРАТНАЯ РЕАЛИЗАЦИЯ

Вопрос об аппаратной реализации поля с распределением потенциала (5) может быть решен за счет создания электродов по форме эквипотенциа-лей поля с заданными уровнями C ₁ и C ₂ :

az ² + P ( x , y ) = C ₁₂. (10)

Принцип работы масс-спектрометра с таким полем описан в работе [20].

Примерная схема ВПМС, в аналитической части которого реализуется поле (9) и, следовательно, имеет место колебательное движение вдоль оси вращения OZ , изображена на рис. 2. Масс-спектрометр содержит импульсный источник ионов 1; электростатический анализатор, представляющий собой пару электродов 2 и 3; детектор ионов 4; входную и выходную щели в анализаторе 5 и 6. Электроды представляют собой поверхности вращения и описываются уравнениями (10) при P = - ar ²/2 + k ln r + const, ( r ² = x ² + y ²). Детектор и источник ионов расположены симметрично относительно плоскости z = 0.

Масс-спектрометр работает следующим образом. Анализируемое вещество ионизуется в источнике ионов и импульсно вводится в аналитическую часть между электродами 2 и 3 через входную щель 5. При прохождении аналитической части первоначальный пакет ионов ( m1 + m ₂ ) разделяется на пакеты m ₁ и m ₂ , соответствующие массовым числам ионов, участвующих в движении, которые, пройдя выходную щель 6, регистрируются детектором ионов в зависимости от массы через интервалы времени t ( m ) = nl^m/ ( 2 qФ₀a ) .

ИДЕАЛЬНАЯ ПРОСТРАНСТВЕННО-ВРЕМЕННÁЯ ФОКУСИРОВКА

Уравнения движения заряженной частицы с массой m и зарядом q в электростатическом поле с потенциалом (9) в цилиндрических координатах X = R cos 9 , Y = R sin 9 , Z = Z имеют вид [21]

дФ mZ = - q---;

дZ дФ

mR = - q--+ mR9

дR дФ M2

■ q --1--;

д R mR ³

M mR ²

где M = mR29 = const — момент количества движения относительно оси OZ . В нормированных координатах и нормированном времени R = r • l , Z = z • l , t = т • T , где выбрано T = l^m^ ( 2 qФ₀a ) , эти уравнения приобретают безразмерный вид

„ q д Ф T²

z = m д z l² = z ’

, ₌ q д Ф T M T ₌ 1 ( A .

r                     72 +    2 73 3 7       ^1 r            l ⁺ 3 ^{; (1Z,)}

m д r l m l r l 2 V r ) r

₉ = MT = ц ml ² r ² r ^{2 ,} где ц = MT,ml ² — нормированный момент количества движения.

Пусть параметры r (0) = r0, r'(0 ) = r0', ц, k/a выбраны таким образом, что решение r (т) второго уравнения системы (12) удовлетворяет условию r(п) = r0. Тогда по истечении безразмерного вре мени т0 = п частицы, стартовавшие с начальными условиями -z0, z‘, r0, r0', ц, окажутся в точке с координатами + z0, r0, т. е. одновременно достигнут детектора независимо от значения параметров z0 и z0 (значение 9(т) в момент прилета т = п несущественно, если детектор сделать кольцевым или если азимутальное движение отсутствует в силу того, что выбрано ц = 0).

В реальной системе значения r0 (z0) фиксируются формой эквипотенциальной линии — поверхности, с которой одномоментно стартуют заряженные частицы, а допустимые значения r0'( z0) и ц( z0) оказываются связаны функциональным соотношением, обеспечивающим выполнение ус- ловия r (п ) = r0. Очевидно, что в безразмерном времени к поверхности детектора (которая строго симметрична к поверхности источника) такие частицы тоже прибудут одномоментно. Физическое время для частиц разной массы, естественно, будет разным (пропорциональным корню квадратному из массы), но все частицы одной массы достигнут детектора строго в одно время, несмотря на разброс начальных параметров. При фиксированной координате z0 (точечный источник) обеспечивается прилет в одну и ту же точку в одно и то же время независимо от угла вылета, контролируемого начальным параметром z‘. Тем самым реализуется режим идеальной пространственно-временнóй фокусировки, по крайней мере, по части параметров пучка, а сама система оказывается эффективным времяпролетным масс-анализатором.

Разброс по параметрам z ₀, z ‘ лимитирован только габаритами электродов и не влияет на идеальность пространственно-временнóй фокусировки. Напротив, разброс по параметрам r ₀, r₀ ' , ц должен подчиняться очень жестким ограничениям, чтобы сохранить идеальную пространственно-временнýю фокусировку. В реальности начальные безразмерные параметры r ₀, r ₀ ' , ц занимают некий фазовый объем, а не бесконечно тонкую фазовую поверхность, соответствующую условию идеальной пространственно-временнóй фокусировки по параметрам z ₀, z ‘ . Поэтому для имеющегося у источника начального фазового объема наблюдается ненулевой разброс безразмерного времени прилета А т ₀, определяемого по пересечению траекторий ( z(т ) , r(т ) ) , стартующих с заданными начальными условиями, с поверхностью детектированиЯ ( z 0 , ^r 0 ( z 0 ) ) , ^{( z} „in <  ^z 0 <  ^z max ). К разбросу А т ₀ следует также прибавить начальный временнóй разброс импульса заряженных частиц, который равен нулю только в идеальном (и никогда не реализуемом) случае бесконечно узкого импульса ионов.

Итоговый разброс А т ₀, собственно, и определяет достигаемое разрешение по массе R = m /А m в соответствии с формулой

А t (m) = t (m + А m) -1 (m) ® пT (А m/ 2 m) > Ат 0 T

(здесь Ат0 , вообще говоря, неявно зависит от массы, поскольку переход от реального фазового объема к безразмерному фазовому объему включает в себя массу). Оптимизируя параметры источника таким образом, чтобы разброс по r0, r0', µ уменьшался за счет увеличения разброса по z0 , z‘, можно основательно уменьшить Ат0 и тем самым увеличить разрешение прибора при сохранении его чувствительности. Минимизация же Ат0 при фиксированном разбросе r0, r0, ц возможна только за счет перестройки структуры поля, т. е. за счет изменения параметра k a (эквивалентно выбору оптимальной стартовой точки для источника) или же за счет перехода от осесимметричного потенциала (9) к более сложным полевым структурам вида (5).

ЗАКЛЮЧЕНИЕ

Таким образом, нами определен класс электростатических полей, в которых осуществляется идеальная пространственно-временнáя фокусировка в направлении разделения ионов по времени пролета. При этом время пролета в значительной степени не зависит от начальных параметров движения частицы и является функцией исключительно параметров выбранного поля. Такими свойствами гарантированно обладают поля с распределением потенциала (5). Среди этих полей существуют поля, легко реализуемые на практике.

ПРИЛОЖЕНИЕ

• I.    Текст авторского свидетельства на изобретение "Времяпролетный масс-спектрометр № 1247973 СССР

• (11 ) 1247973

• (51)    4 H 01 J 49/40

• (21)    3840525/24-21

• (22)    16.01.85

• (71)    Институт аналитического приборостроения Научно-технического объединения

АН СССР и Ленинградский политехнический институт им. М. И. Калинина

• (72)    Л.Н.Галль, Ю.К.Голиков, М.Л.Александров, Е.Э.Печалина и Н.А.Холин

• (53)    621.384

• (54)    (57)

• 1.    ВРЕМЯПРОЛЁТНЫЙ МАСС-СПЕКТРОМЕТР , содержащий импульсный источник ионов, анализатор, состоящий из двух коаксиальных электрически разделенных электродов и детектор, отличающийся тем, что с целью повышения разрешающей способности и чувствительности, упрощения конструкции при одновременном уменьшении габаритов, электроды анализатора выполнены в виде симметричных относительно плоскости Z ^ 0 поверхностей, описываемых уравнениями

( — "1²

I "Т I + Р ( x , У ) = С , 2 ,

• V d 7

где d — длина пролетной части масс-спектрометра вдоль оси Z ;

p ( x , у ) — произвольная функция, удовлетворяющая уравнению

• д2 p д2 p2

• _ 1 + _ 1 =

• дx2   ду22

• 2.    Масс-спектрометр по п. 1, отличающийся тем, что, с целью упрощения изготовления электростатической системы, электроды выполнены в виде квазиконических поверхностей с общим основанием, описываемых уравнениями

  —у di 7

  
  

  = С 1,2 ,

  
  
  
  
  

C ₁ и C ₂ — постоянные, характеризующие поперечный размер электродов.

Примечание. Текст публикации в "Бюллетене изобретений" воспроизведен аутентично, т. е. со всеми имеющимися неточностями. В частности, следует отметить фразу "симметричных относительно плоскости Z Ф 0" вместо

"симметричных относительно плоскости Z = 0", член "

—

ln y d

" в формуле для осесимметричного варианта

2 + 2

масс-спектрометра вместо очевидного " + kln——", старт и детектирование ионов из бесполевого пространства d вне электродов анализатора, показанные на рисунке, отчетливо огрубленную форму электродов на рисунке.

• II.    Вид авторского свидетельства на изобретение "Времяпролетный масс-спектрометр" № 1247973 СССР

  

  Рис. 3.

  
  

СОЮЗ СОВЕТСКИХ СОЦИАЛИСТИЧЕСКИХ РЕСПУЬЛИК

ГОСУДАРСТВЕННЫЙ КОМИТЕТ СССР ПО ДЕЛАМ ИЗОБРЕТЕНИЙ И ОТКРЫТИЙ 1ЮКЮЕ анииюво

На основании полномочий, предоставленных Правительством СССР, Государственный комитет СССР по делам изобретений и открытий выдал настоящее авто] 'Врешшролетшй масс-сп на изобретение:

Автор (авторы): Галль Лидия Николаевна, Голиков 10рий Константинович , Александров Максим Леонидович, Печалила Елена Эдуардовна и Холин Николай Алексеевич

Приоритет изобретения 16 Января 1985г Зарегистрировано в Государственном реестре изобретений СССР 1 апреля 19861?.

Действие авторского свидетельства распространяется на всю территорию Союза ССР.

Предсейитмъ Колите»!