Об одном классе определяющих соотношений пластичности

At quasy-linear formulation of the constitutive equations three types independent gyroscopic forces for deformation processes are considered. Most interesting for mechanics and thermodynamics is the construction of the uniform functional constitutive equations, work-conjugated with the equations of some main process. The postulates of plasticity are not used. Isomorphism idea leads to such form of functional equation, that allows already on stage of construction of the functional equation as a whole to define structure of constitutive functionals of process.

В основе рассмотрений здесь находится идея А.А. Ильюшина о построении уравнений состояния как решений функциональных уравнений термодинамики[1]. Поскольку в теории пластичности наиболее хорошо изученными являются процессы простого нагружения и близкие к ним и строго доказано, что эти процессы возникают в материале при вполне определенных и технологически достижимых физических условиях, то важно изучить функциональные окрестности этих процессов как решения функциональных уравнений, определив и изучив классы процессов, которые математически являются «близкими к простым» или «приводимыми к простым».

В тех случаях, когда все скалярные функционалы состояния, входящие в функциональные уравнения связи напряжений и деформаций, заданы вдоль траектории процесса, то при помощи процедуры перенормировки пространств напряжений и деформаций [3], за счет специального выбора функционалов-метрик достигаются упрощение функциональных уравнений и интегрирование их вдоль траекторий процессов. Поэтому существуют классы процессов со сложными функциональными уравнениями в пространстве напряжений-деформаций, которые в этом смысле являются приводимыми к простым.

В качестве физического источника, которое определяет структуру функционального соотношения между термодинамическими силами и потоками, возьмем основное термодинамическое тождество [2].

Пусть σ – тензор напряжений Коши, а ε ˆ – парная ему термодинамическая координата, используемая в качестве меры деформаций. Выражение скорости совершения работы силами внутренних напряжений представим в виде скалярного произведения шестимерных (пятимерных, если шаровые компоненты тензоров отделены) векторов напряжений σ и деформаций ε : δ A ≡ σ ˆ : δε ˆ = σδε . В этом равенстве δε ˆ ≡ sym( ∇ V ) δ t обозначает соответствующую временную коротационную вариацию от меры деформаций.

Если функционал состояния дифференцируем по Фреше, то в процессе нагружения

δε

σδε = σ δσ ≡ σ P ˆ ^{- 1} δσ . δσ

Отсюда следует, что o ( S8 - P ¹8с ) = 0 и существуют классы эквивалентных процессов нагружения с общим представлением скорости совершения работы силами внутренних напряжений.

Это обстоятельство позволяет использовать методику построения и исследования функциональных уравнений пластичности, предложенную А. А.Ильюшиным в [1]. Для начально-изотропного материала функциональное уравнение n-le— Ге— (°, So) _^

5s = P So + al So--o I ,

V o )

содержащее два скалярных функционала состояния P и a, определяет по А.А.Ильюшину процесс в пространстве деформаций или напряжений. Второе слагаемое в функциональном уравнении ортогонально вектору напряжений и поэтому не совершает работы в процессе нагружения. Если потребовать, чтобы функциональные уравнения удовлетворялись точно на процессе 8 = 8o / o, то получим условия, которые в функционалы P и a:

процессе простого нагружения определяют скалярные a=

N

1, N = o, P = *. P 8 S8

При этих условиях процесс простого нагружения точно удовлетворяет функциональному уравнению. Естественно при изучении процессов, которые принадлежат некоторой функциональной окрестности основного процесса класса, определяемого функционалом P, так же считать a = 1/ N -1/ P, а скалярные функционалы N и P произвольными, но на траекториях основного процесса (процесса простого нагружения) совпадающими с функционалами процесса простого нагружения. В этом случае получим известную трехчленную формулу [1]

S8 = —So +

N

1    1 ) ( o , So )_

---I------т----o, P N) o2

и формулу, обратную к ней,

So = N S8 + ( P - N )^(oM o .

o

Заметим, что соотношение (1) получено включением в уравнение основного процесса дополнительного слагаемого, не совершающего механической работы (гироскопического). С другой стороны, обратное соотношение (2) такой интерпретации не имеет. Отметим также, что при тензорно линейной формулировке уравнений состояния возможны три вида независимых гироскопических сил:

( о , ^{So )}        ( о , ^{S8 )}       ( о , Ё )

So--2— o, S8--2— o, 8--2— o, o         o        o позволяющих строить аналогичные (1), (2) соотношения.

В лагранжевой механике наиболее удобны голономные меры деформации, поскольку с их помощью легко записывать внутреннюю энергию и, следовательно, лагранжиан. Согласно [4] в механике необратимых процессов сред с внутренними степенями свободы в вариационное уравнение Лагранжа, помимо вариации лагранжиана, входят вариации функционалов, характеризующих взаимодействия частиц среды со своим окружением и внешними полями. Эти функционалы в теории играют роль обобщенных сил. Включить такие силы в лагранжиан полностью, как правило, невозможно по причине неголономности их вариаций.

В [4] также отмечено, что при создании новых моделей, когда уравнения состояния только устанавливаются, вопрос о возможности разного выбора уравнений состояния возникает по существу. При этом уместно использовать и дивергентную неоднозначность напряжений, и гироскопические обобщенные силы, не изменяющие внутренней энергии, но входящие в уравнения Лагранжа, и другие возможности в качестве инструмента математического моделирования. Таким образом, накопленное знание о деформируемых средах (механическое, металловедческое, физическое и др.) в идеализированном виде включается в лагранжиан, а нечеткое знание — в виде "обобщенных сил", особенно "обобщенных гироскопических сил".

Изоморфные описания процессов деформации и нагружения

Наиболее интересным с точки зрения термодинамики и изоморфизма описаний процессов деформаций и нагружения является построение единых функциональных уравнений, термодинамически согласованных с уравнениями некоторого основного процесса. Не используя постулатов пластичности, но наделяя изоморфизм описания конкретным смыслом, в этом разделе построено единое функциональное уравнение в вариациях. Использование такого подхода позволяет уже на этапе построения функционального уравнения в вариациях во многом определить структуру определяющих функционалов. Различные возможности изоморфизмов порождают различные (числом и типом определяющих функционалов) функциональные уравнения. Ниже подробно рассмотрен подход, при котором число функционалов равно трем.

Определение изоморфизма

Найдем функциональное уравнение, которое описывает процесс нагружения и отличается от уравнения основного процесса членами, не совершающими работы в процессе нагружения. Так же потребуем, чтобы уравнение одновременно описывало и обратный процесс (процесс деформаций) и при этом отличалось от уравнений основного процесса слагаемыми, не совершающими работы в процессе деформаций. В этом случае единым функциональным уравнением будет установлен изоморфизм пространств напряжений и деформаций.

Прямое и обратное векторно-линейные уравнения состояния, полученные гироскопическим возмущением уравнений основного процесса, имеют вид бй = Р1ба + /бй - I^:6^) + B[бё - (^j^ V         а2 у Vа

+ ( C 1 ( й , бй ) + C ₂( й , ба ) + C ₃ ( а , бй ) + C ₄ ( а , ба ) ) | й - ^{( й} , ^{g ) g} V а ²

( й , бй ) й) ..[„_ ( й , ба ) й)

Pба = бй + KI бй -     2    I + LI ба -    2I +

V й у V й у

+ (M 1 (й, бй) + M2 (й, ба) + M3 (а, бй) + M4 (а, ба)) а - (й’ ^ Vй

Каждое из этих соотношений состоит из десяти слагаемых, пропорциональных бй, й(й, бй), й(й, ба), й(а, бй), й(а, ба), ба, а( й, бй), а(й, ба), а(а, бй), а(а, ба).

Отметим, что функционалы основного процесса P и P 1 в прямом и обратном уравнениях состояния не предполагаются одинаковыми (но это возможно), а физический смысл введения гироскопического возмущения в основное термодинамическое тождество имеет только второе из уравнений. Отождествляя уравнения прямого и обратного процессов, получим нелинейную систему 10 уравнений для 14 скалярных функционалов:

A -1 = 1 + K, P1 + B = - P + L,

-

- с з

A

£ ²

C 1 = ^-

-

K	- м 1 ( 5 , — ), с 2 =- -L^ - м,
2
а	аа
M 3	( а , — )               ( а , — ) 2 , с 4 = - м 4   2 , - с 1
	а 2               а 2
C 3	( а , — )          B г ( а , — ) 2 = м 3 ,   2 с 4    2

= M ₄.

^{( а} , ^— ) а ² (О— ) £ ²

,

= M 1 , - C 2^- = M 2 , £ ²

Вводим обозначения n _а и n _£ для направляющих векторов напряжений и деформаций, Т = 1 - ( n _а , n _£ )². В результате решения нелинейной системы получается связь между функционалами и новая форма функционального уравнения:

5а = { P -Т ( Т + P П — ) } 5—+ T ( n а , 5— ) { n _а- n — ( n _а , n — ) } +

^{+ P П} £^{({ (} n £ , ^5— ) ^{- (} n а , n £ ⁾⁽ n а , ^{5— ) }} n £ ^{+ { (} n а , ^5— ) ^{- (} n а , n — ⁾⁽ n — , ^{5— ) }} n а ) содержащая три свободных скалярных функционала состояния P , П_£ = ( AP 1 + B )/( A - 1)/ Т , и T = ( P - P 1 )/ Т .

При P = Р₁ отсюда следует функциональное уравнение

5а = P { 1 -ТП_£ } 5—+

^{+ P П} —^{({ ( n} — , ^5— ) ^{- ( n} а , ⁿ — ^{)( n} а , ^{5— ) } n} — ^{+ { ( n} а , ^5— ) ^{- ( n} а , ⁿ — ^{)( n} — , ^{5— ) } n} а ) , содержащее два функционала состояния P и П_£ .

В процессе простой деформации — / — = а / а = n имеет место связь между вариациями

5а _ 5а „5— _ 5— _А --а—= 0,-- £-г = 0, а а ²       £ £ ²

из которой следует функциональное уравнение процесса

• 5—    = ^—5— = —5г = —5а .

£ а 5а

Это же уравнение следует из (4) и определяет обычный смысл функционала P в процессе простой деформации, поэтому теория малых упругопластических деформаций удовлетворяет функциональному уравнению (4). В [3] показано, что различные теории течения с изотропным и кинематическим упрочнением также удовлетворяют этому уравнению. Поскольку функциональное уравнение получено только установлением изоморфизма, но без использования постулатов пластичности, то законы трансляции и упрочнения поверхности текучести задаются конкретными функционалами, что может использоваться при идентификации функционалов.

Об определяющих функционалах

В функциональные уравнения (3), (4) входят определяющие функционалы P , T , П_£ , и решение уравнения невозможно без установления конкретного вида функционалов для различных классов траекторий деформаций. Рассмотрим, например, широкий класс частных решений уравнения (4) вида

_ _{п п} _ о - -   5— _     1 5 n _     1 5 n₂

- + — n 1 , 5 5 = |5—I , К 2

направляющие векторы траектории деформаций,

• ⁿ а = Р 1 n 1 + ₽ 2 n 2 +Р з n 3 , ⁿ 1 = —, ⁿ 2 =--—, ⁿ 3 =--—

55       к, 55        к 2 55

здесь Ki обозначают кривизны траектории деформаций, n|, n2, n3 являются ортогональными единичными векторами нормали и бинормали, связанными уравнениями Френе [1]. Направляющие косинусы направляющих векторов напряжений и деформаций в репере Френе обозначены через Pi = cos 9i и уi = cos фi.

Вычисляем производную напряжений и подставляем в уравнение (4). Получим векторное соотношение

5o _/5(P1o)     _ 1 _/5(Р2о)     _

— = n i ^       ^K i P 2 a U n 2 ^   -- + ^a ^- к 2 P 3 ^a I +

55   155      1155I

+ n3 I 5(^30) + к2^2° I + (^3a)K3n4 I 55I

= P n_s

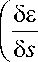
-P i ⁵p I n _e +

/

P - P П_е< 1 - 5p V

² -P i I P i

-

5s

sp

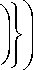
n _i +

.    „ U 5s V „ U 5s V

^{+ P n} s P 2 I P i ^- —⁵P I ⁿ 2 ^{+ P n} s P 3 I P i ^- — ⁵P I n 3 , ⁵P =P i ^cos Ф i .

V 5 5 J             V 5 5 J

С точностью до члена, пропорционального третьей кривизне траектории деформаций, отсюда следует представление направляющего вектора деформаций ns в неполном репере Френе n1,n2,n3. Поэтому сделанное предположение о характере решения функционального уравнения (4) сужает класс возможных траекторий деформаций до трехмерных траекторий деформаций.

Из векторного уравнения следует система трех скалярных соотношений:

^{5 ( в 1 а ) - К} 1 Р 2 ^a = ^{P + P n} s { ⁽ Y i ^- P i ⁵Р ) Y i ^{- (i - 5}Р ^{2) +} P i ⁽ P i ^- Y i ⁵Р ^{) }} ,

^{5 ( в 2 a ) + K} i P i ^{a - к} 2 Р 3 ^a = ^{P n} s ^{{ (} Y i ^- P i ⁵Р ) Y 2 ⁺ P 2 ⁽ P i ^- Y i ⁵P ^{) }} , 5 5

^{5 ( в} 3 ^{О ) + к} 2 Р 2 ^a = ^{P n} s ^{{ (} Y i ^- P i ⁵Р ) Y 3 ⁺ P 3 ( P i ^- Y i ⁵P ^{) } .} 5 5

Функционал P определяется прямо из уравнения (4):

I- 5a)    _ 5s) _n 15o) i

.

И --- — г И -- \ г — -- ----- n a ,              n 0 ,      ,

V    5 5 J    V    5 5 J     V 5 5 J cos 9 _i

После преобразований система уравнений приводится к виду

| ^^ -кР₂ |a—-—(i -в ²) = - Р П (cos9₃ cos9₂ - cos9₂ cosф₃)²,

<& ^{i 2} J   p _i &                ^{b 3     2       2     3}

| ^2 + K _i P _i -k ₂ P ₃ |a+P₂ — =- Р П_е (cos 9 _icos ф ₃ - cos 9 ₃ cos ф _i)(cos 9 ₃ cos ф ₂ - cos 9 ₂cos ф ₃),

^3 + к ₂ р ₂ р+Р ₃ — = Р П_е (cos 9 _icos ф ₂ - cos 9 ₂cos ф _i)(cos 9 ₃cos ф ₂ - cos 9 ₂cos ф ₃).

Поскольку уравнения системы линейно зависимы, то из нее следуют два соотношения, определяющие углы сближения 9i, 92, не содержащие функционала Пе. Третий угол определяется из условия нормировки.

В частном случае, когда направляющие векторы напряжений и деформаций лежат в плоскости векторов n _i, n ₂(cos 9 ₃ = cos ф ₃ = 0), система уравнений удовлетворяется для любого функционала П _е при условии

59i        _о i 5о _п

— ^{+ к} + tg ⁹i- — = 0,                              ⁽5)

5 5           a 5 5

определяющем зависимость угла сближения от интенсивности напряжений (или от длины дуги траектории деформаций). Отметим, что полученное соотношение по форме совпадает со следствием трехчленной формулы, но место функционала N в ней занимает функционал P . Это обстоятельство было причиной введения второго основного функционала P1 . Тем не менее при выборе даже постоянного значения для функционала Па на траекториях деформаций с прямолинейным участком удается точно описать экспериментальную зависимость угла сближения направляющих векторов напряжений и траектории деформаций от длины дуги, установленную

Р.А.Васиным [6].

Аналогичное соотношение для функционального уравнения (3) имеет вид

— + к + tg 91

112- T а 5 5 а

•а 5a Q sin 9--cos 9i

¹ 5 5           ¹

1 -f?)

I 5 5 )

5а

.

Поскольку функционал T созвучен разности ( P - N ) в трехчленной формуле, то последнее соотношение (6), а следовательно, и уравнение (3) являются предпочтительными для траекторий с прямолинейным участком.

Замечание.

Условие ( n _а , 5а ) - ( n _а, n _а )( n _а, 5а ) - 0 исключает из уравнения (4) слагаемое, содержащее направляющий вектор деформаций. Поэтому, если в некоторой точке траектории деформаций векторы n _а и 5а / 5 5 коллинеарны, то вектор приращения напряжения также будет им коллинеарным (в соответствии с экспериментами В.С. Ленского). Поэтому предположение о локальной простоте процесса деформаций, сделанное В.И. Малым в [5], хорошо согласуется с уравнением (4).