Об одном методе интерполяции таблиц смертности для дробных возрастов

Как мы знаем, использование таблиц смертности, предоставляемые национальным статистическим комитетом Кыргызской Республики (КР) [3] сложно применять в реальных задачах страхования, из-за отсутствия данных для дробных возрастов. Для их применения необходимо составить более подробные таблицы смертности для случая дробных возрастов, что существенно затрудняло работы до появления современных технологий. Естественно, что на сегодняшний день существует множество программ, которые с легкостью помогут в построении таблиц смертности для дробных возрастов, с учетом данных таб- s(x + t) = (1 — t)

здесь s(x + t) - число доживших до возраста x + t - лет, x - целое число лет, а t - это дробная часть возраста, т.е. 0 < t < 1. Данная интерполяционная формула является наиболее простым. Более сложный формулы интерполяции, это показательная интерполяция [1] lns(x + t) = (1 — t) lns(x) + t • lns(x + 1), и гармони- лиц смертности для целых возрастов. Таблицы смертности применяются в задачах связанных с страхованием жизни, статистикой и многими другими направления математики и экономики в целом. Много примеров приведены в книгах Бауэрса Н., Гербера Х., Джонса Д., Несбитта С., Хикмана Дж. [1], Фалина Г. И., Фалина А. И. [2], [4] и [5].

Для определения значений таблиц смертности дробных возрастов существует множество формул интерполяции. Например, самая простоя из них, это линейная интерполяция, где формула имеет следующий вид [1]:

• • s(x) + t • s(x + 1)

ческая интерполяция (гипотеза Бальдуччи) 1 1-t t

• ^[1]    — — ' *+» • ^{Но данные методы} интерполяции имеют выпуклость вниз в искомой области определения. Для определения нового метода интерполяции сначала давайте построим саму таблицу смертности Кыргызстана.

  

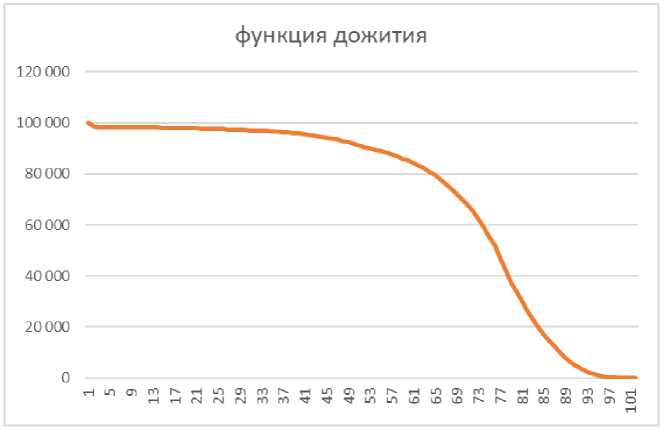
  Рис 1. График функции дожития для КР 2016-2020 гг.

  
  

Если исследовать график функции дожития, то можно заметить, что данный график, имеет выпуклость вверх в области от 5 лет до 80 лет. Но все формулы интерполяции приведенные выше имеют выпуклость вниз. И данный график имеет пара- болический вид. Учитывая данные факты введем новое определение.

Определение 1. Интерполяционная формула для определения функции дожития для дробных возрастов определяемая по формуле

s2(x + t) = (1 — t) • s2(x) + t • s2(x + 1)

где 0 < t < 1, x E Z + назовем параболической интерполяцией .

Важно помнить, что s(x) - является известным из таблицы смертности КР, для целых значений х. Параболическая интерполяция, является убывающей функцией.

Притом данная функция имеет выпуклость вверх.

Чтобы показать, что функция (1) убывает, преобразуем функцию к следующему виду

s2(x + t) = s2(x) — t • (s2(x) — s2(x + 1))                       (2)

Как видно выражение s2(x) — s2(x + 1) в формуле (2) всегда положительна т.к. s(x) > s(x + 1). Тогда соответственно с ростом t значение функции s2(x + t) бу дет убывать. Приведем доказательства убывания функции, для этого выразим формулу (2) функции дожития, в следующем виде

s(x + t) = /s2(x) — t • (s2(x) — s2(x + 1))                      (3)

Найдем производную функции (3)

s‘(x + t) =

s2(x) — t • (s2(x)

—

s2(x + 1)

>)'=

(s2(x) — t • (s2(x) — s2(x + 1)))          —(s2(x)

— s2(x + 1))

2js2(x)

— t • (s2(x) — s2(x + 1))

2^2

(x) — t • (s2(x)

— s2(x + 1))

S2(x + 1) — S2(x)

2 ^s2(x) — t ■ (s2(x) — s2(x + 1))

Здесь знаменатель всегда положительна, а числитель s2(x + 1) — s2(x) < 0, т.к. s(x) > s(x + 1), соответственно т.к. производная отрицательна в области опреде- ления функция дожития всюду убывает, что и требовалось доказать.

Вычислим вероятности дожития человека в возрасте х до возраста х + t, с учетом параболической интерполяции (3)

s(x + t)   Js2(x) — t ■ (s2(x) — s2(x + 1))

s(x)                  s(x)

t ^p x

J

S2(x) — t ■ (s2(x) — s2(x)

s2(x + 1))

tPx = V1—t(1 — pX) = 71 — t +t ■ pX

Теперь вычислим вероятности смерти человека в возрасте х в течении дробного времени t

s(x) — s(x + t)

t9x =      S(X)      = 1 — tPx

tQx = 1 — V1 — t + t ■ pX

Полученные формулы для определения вероятности дожития до возраста х + t, и вероятности смерти человека в возрасте х в течении времени t.

Новая формула интерполяции может применяться для решения задач страхования жизни, и страховых аннуитетов. Также его можно использовать в обучении дисциплине теории вероятностей в страховании, актуарной математике и пенсионном страховании. В дальнейшем мы будем исследовать свойства данного метода интерполяции и его применение в страховании и экономике.