Об одном методе исследования коэффициента температурного расширения полимеров

ВЕСТНИК ПНИПУ. МЕХАНИКА № 2, 2024PNRPU MECHANICS BULLETIN

Современные подходы к проектированию изделий, основанные на математическом моделировании, включающем описание термомеханического поведения конструкций в широких температурных диапазонах, требуют как можно более полной информации о физико-механических свойствах материалов, зачастую в виде функциональных зависимостей их значений от температуры и других параметров окружающей среды.

На сегодняшний день широкое распространение во всех отраслях промышленности получили полимеры, обладающие, по сравнению с другими конструкционными материалами, целым спектром уникальных эксплуатационных характеристик и большим разнообразием технологических параметров. Однако известно [1], что физико-механические свойства полимеров значительно зависят от температуры и истории ее изменения, релаксационных процессов, скоростей деформаций, напряженного состояния и др.

В некоторых случаях, например, в волоконно-оптических датчиках, термомеханические процессы в за-щитно-упрочняющих полимерных покрытиях (ЗУП), нанесенных на световоды, используемые в качестве чувствительных элементов, могут оказывать значительное влияние на точность измерений и в целом на эксплуатационные характеристики таких изделий [2; 3].

Кроме того, ряд эмпирических исследований показал, что выбор материала ЗУП, использование многослойной конструкции и даже соотношение толщин полимерных покрытий в них могут существенно влиять на чувствительность волоконно-оптических датчиков к изменению температуры, в одних случаях улучшая, в других ухудшая их эксплуатационные характеристики [4-9]. Точность чувствительных элементов таких сенсорных систем зачастую обусловлена специально сформированным напряженно-деформированным состоянием (НДС). Одним из параметров, влияющих на НДС в оптическом волокне чувствительного контура, является КЛТР полимеров ЗУП. В связи с этим необходимо определение закономерностей влияния температуры на КЛТР полимеров, методики его измерения и построение функциональных зависимостей, учитывающих условия и характер эксплуатации конкретных изделий.

Исследованиям зависимости КЛТР от различных параметров посвящен ряд работ, в частности, в статье А.И. Слуцкера с соавторами [10] описано исследование температурной зависимости термического расширения поливинилацетата (ПВА) в области релаксационного перехода. В работе Р. Хувинка и А. Ставермана [11] приведены экспериментально полученные зависимости удельного объема как функции температуры для полиметилметакрилата. В работе Р.С. Спенсера [12] исследовано влияние температуры и скорости охлаждения на удельный объем полистирола, приведены экспериментальные данные и получена аналитическая зависимость. В работах [13; 14] Д.М. Хатчинсон и А.Д. Ковакс исследуют зависимость температурного расширения стекол от истории температурного воздействия.

В работе [15] методами натурного эксперимента А.Н. Труфановым и И.Н. Шардаковым было показано, что деформационный отклик пленочных полимерных образцов на температурное воздействие зависит не только от температуры, но и от скорости ее изменения. А в общем случае в условиях цикличного нагрева и охлаждения при одинаковых абсолютных значениях температуры КЛТР полимеров может отличаться на десятки процентов [15–17].

Температурная деформация полимеров обусловлена существенным вкладом как ангармонических колебаний атомов, так и конформационными эффектами, связанными с проявлениями сегментальной подвижности цепей и межмолекулярным взаимодействием; если первый механизм практически не имеет инерции, и эта составляющая температурного расширения синфазно следует за изменением температуры [18], то конформационные переходы, как известно, развиваются в материале с течением времени, которое обусловлено характерными временами релаксации, зависит от температуры и от истории ее изменения [1; 11].

Таким образом, можно утверждать, что температурная зависимость коэффициента термического расширения полимеров носит сложный нелинейный характер, является функцией не только температуры, но и скорости ее изменения, что особенно ярко проявляется в интервалах, включающих терморелаксационные переходы в материале. На сегодняшний день в литературных источниках эта проблема не раскрыта в полной мере. Следовательно, в рамках описанной проблематики актуальна задача разработки новых подходов и методик исследований, позволяющих на основе экспериментальных данных строить математические модели, адекватно описывать наблюдаемые на практике эффекты, давать качественную и количественную оценку температурных деформаций полимеров с учетом истории изменения температуры.

В представленной работе предложена методика идентификации температурной зависимости КЛТР для пленочных полимерных образцов. Предлагаемые в рамках исследования подходы востребованы для математического описания термомеханического поведения УФ-отверждаемых полимеров, которые в виде различных пленочных покрытий широко используются в оптоволоконных приложениях. В настоящее время в расчетных схемах используют, как правило, не зависящие от температуры осредненные на некотором интервале значения КЛТР для высокоэластичного и застеклованного состояний [19; 20], что не позволяет в полной мере учитывать влияние полимерных покрытий на привносимые погрешности в волоконно-оптических датчиках, обусловленные происходящими в них термомеханическими процессами и их влиянием на НДС в оптическом волокне.

1.    Пробоподготовка и методика измерений

Для натурных экспериментов изготавливались пленочные образцы по следующей технологии: небольшое количество жидкой фотополимеризующейся композиции или эпоксидной смолы наносили на лист полиэтилентерефталатной пленки, накрывали другим листом и прижимали грузом для формирования тонкого слоя. Далее образцы из УФ-отверждаемого полимера размещали под источником УФ-излучения на время, необходимое для формирования рекомендованной производителем экспозиции, а образцы из эпоксидных смол нагревали до температуры полимеризации. Затем из отвержденного полимера вырубным прессом (рис. 1) вырезали образцы необходимых размеров и удаляли ПЭТФ-пленку. Характерные размеры полученных образцов 20×6,25 мм и толщиной 0,05-0,250 мм.

Рис. 1. Вырубной пресс для формирования образцов из заготовок пленок и пластин

Fig. 1. Cutting press for forming samples from films and plates

Традиционные методы измерения КЛТР с помощью дилатометра для рассматриваемых полимеров оказались неприменимы, так как получаемые образцы в виде пленок из УФ-отверждаемого полимера имеют недостаточную толщину и в высокоэластичном состоянии обладают относительно невысокой жесткостью [21]. Методы лазерной интерферометрии [22], нейтронной рефлектомет-рии [23], спектральной эллипсометрии [24], x-ray-ре-флектометрии [25], ёмкостной дилатометрии [22; 26] имеют высокую точность измерений и позволяют исследовать пленки. Однако в силу конструктивных особенностей при использовании этих подходов достаточно сложно реализовать скорости изменения температуры выше 5 ° С/мин, обеспечить равномерность поля температур в образце, а для исследования образцов в области низких температур требуется еще более сложная технологическая оснастка.

В связи с перечисленными выше факторами в представленном исследовании для измерения температурных деформаций пленочных образцов использовался дина- мический механический анализатор (ДМА), который имеет специализированные захваты (рис. 2); позволяет задавать температуру в широком диапазоне, регулировать скорость ее изменения; осуществлять точный контроль прикладываемой силы и измеряемых перемещений; позволяет корректно работать с пленочными образцами. Кроме того, на одном и том же образце можно получить данные и для анализа температурного расширения, и для определения вязкоупругих характеристик. Аналогично модулированию температуры можно получить дополнительную информацию, исследуя отклик исследуемых образцов при изменении температуры с разной скоростью.

Рис. 2. Внешний вид оснастки для закрепления пленочных образцов

Fig. 2. The appearance of the clamps for fixing film samples

Экспериментальные исследования выполнялись на ДМА марки TA Instruments Q800, точность измерения которого 1 нм для перемещений и 10 мкН для усилий, что с учетом описанных выше характерных размеров рассматриваемых образцов дает возможность получать корректные данные по их температурной деформации. Для расширения температурного диапазона в область отрицательных температур использовалась система охлаждения жидким азотом GCA, позволяющая проводить эксперименты в интервале от - 150 до 600 ° С.

Эксперименты проводились по следующему алгоритму: сначала образцы нагревались и выдерживались до 30 мин при температуре на 20-30 °С выше температуры стеклования для того, чтобы снять возможные остаточные напряжения и другие эффекты, связанные с историей их изготовления и хранения. После этого образец медленно (1 °С/мин) охлаждался до температуры верхней границы рассматриваемого диапазона. Исследования выполнялись в режиме контролируемой силы, величина которой подбиралась минимально возможной в диапазоне от 0,001 до 0,005 Н, такой натяг необходим, чтобы обеспечить прямолинейную геометрию образца в течение эксперимента. После приложения нагрузки при температуре верхней границы исследуемого диапазона до начала процесса изменения температуры выдержи- вали образец до полного завершения протекающих в образцах релаксационных процессов, окончание которых определялось по выходу на «полку» зависимости деформации от времени. Далее образец охлаждали до нижней границы диапазона с постоянной скоростью, выдерживали также до выхода деформации на «полку» и нагревали с той же скоростью до начальной температуры. По окончании нагрева образцы выдерживали при постоянной температуре до стабилизации деформации. На протяжении всего эксперимента фиксировались перемещения, температура и усилие.

Характерные кривые для пленочного образца из эпоксидной смолы EPO-TEK-330, полученные в рамках натурного эксперимента, выполненного в соответствии с описанной выше программой, представлены на рис. 3. Скорость изменения температуры в первом цикле «нагрев – охлаждение» - 10 ° С/мин, 5 ° С/мин во втором и 2 ° С/мин в третьем. Размеры образца 21,83×6,25×0,0367 мм. Эксперимент выполнялся в условиях контролируемой силы натяжения F н = 0,001 Н.

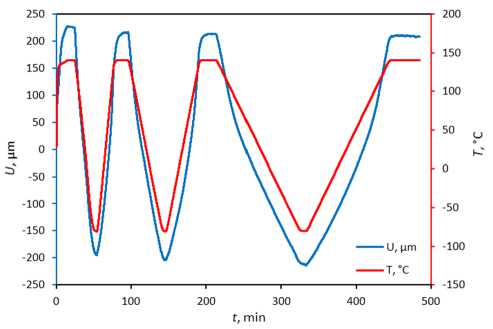
Рис. 3. Фиксируемые в эксперименте изменения перемещений и температуры; полимер EPO-TEK-330; скорость охлаждения/ нагрева 2, 5 и 10 °С/мин; размер образца 21,83×6,25×0,0367 мм;

контролируемая сила натяжения F н =0,001 Н

Fig. 3. Displacement and temperature recorded in the experiment; EPO-TEK-330 polymer; cooling/heating rate 2 °С/min; sample dimensions 21,83×6,25×0,0367 mm; controlled tension force 0,001 N

Видно, что деформационный отклик образца зависит не только от температуры, но и от скорости ее изменения, что еще более заметно на графике зависимости деформации от температуры (рис. 4). Очевидно, что чем больше скорость изменения температуры, тем больше расстояние между кривыми, соответствующими нагреву и охлаждению.

Практика использования ДМА для измерения КЛТР пленок и пластинок показала, что необходимо учитывать температурную деформацию оснастки для ее компенсации в получаемых экспериментальных данных. Для этого были выполнены эксперименты на образцах в виде пластинок разной длины из чистого кварцевого стекла с характерными размерами: ширина 3,01 мм, толщина 0,558 мм и длина от 4 до 22 мм.

Чистое кварцевое стекло обладает одним из самых низких коэффициентов температурного расширения в достаточно широком температурном диапазоне. Характерные значения КЛТР кварцевого стекла (SiO 2 ) в рассматриваемом температурном диапазоне а = 5 • 10 - 7 К ^{- 1} [27; 28], что в 30–50 раз меньше значений для нержавеющей стали, из которой выполнена оснастка. Таким образом, в результате испытаний мы напрямую получим деформацию оснастки, которую можно уточнить, рассчитав по известному КЛТР деформацию кварцевого стекла.

На рис. 6 отражены те же данные в координатах «перемещение – температура» для образца длиной 22 мм. Синим цветом обозначено охлаждение, красным - нагрев со скоростями 2, 5 и 10 ° С/мин. В отличие от пленочных образцов (см. рис. 4.) рост температуры сопровождается отрицательными перемещениями. При скорости изменения температуры 2 ° С/мин кривые, соответствующие нагреву и охлаждению, достаточно близки друг к другу, однако с увеличением скорости изменения температуры разница становится существенной.

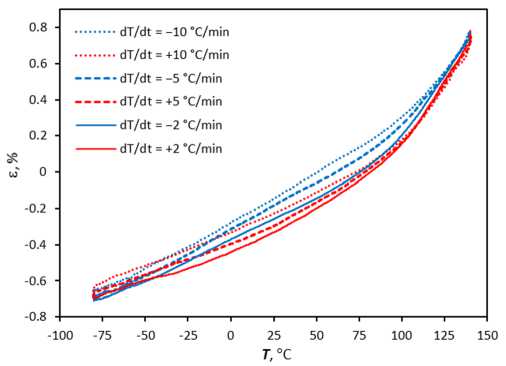
Рис. 4. Зависимость деформации от температуры для полимера EPO-TEK-330 для разных скоростей изменения температуры; толщина образца 36,7 мкм

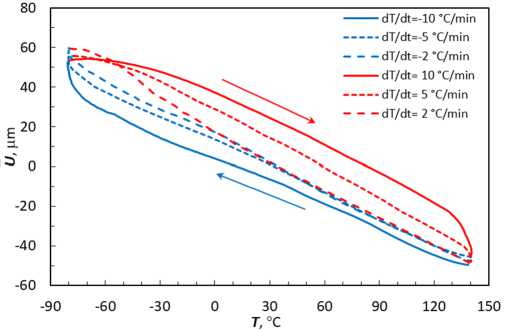
Рис. 6. Зависимость перемещений от температуры для образца из кварцевого стекла длиной 22 мм при разных скоростях охлаждения/нагрева

Fig. 6. Temperature dependence of displacements for a silica glass sample with a length of 22 mm at different cooling/heating rates

Fig. 4. Temperature dependence of strain for EPO-TEK-330 for different cooling/heating rate; sample thickness 36,7 microns

В соответствии с описанной процедурой по программе, аналогичной приведенной на рис. 3, выполнялся эксперимент c образцами, изготовленными из тонких кварцевых пластин, такой же длины, как рассматриваемый образец. Полученные результаты показаны на рис. 5.

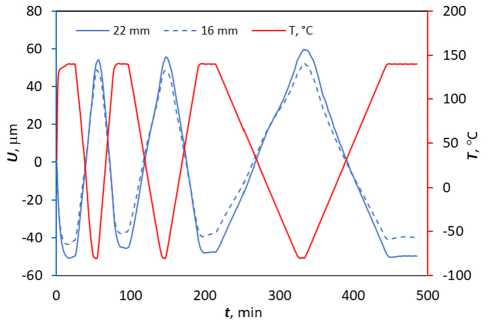
Рис. 5. Температурная деформация в натурном эксперименте с образцами из чистого кварцевого стекла разной длины: 22 мм (сплошная), 16 мм (пунктир)

Fig. 5. Temperature deformation in a full-scale experiment with samples of silica glass of different lengths: 22 mm (solid), 16 mm (dash)

Как видно по конструкции оснастки (см. рис. 2), за счет разницы в высоте верхней траверсы и нижнего зажима при нагреве расстояние между ними увеличивается, возникает дополнительное растягивающее усилие в образце. В режиме контролируемой силы ДМА компенсирует растяжение, выдвигая нижний захват, регистрируя это как отрицательные перемещения в образце, так как именно на этом плунжере установлен оптический датчик перемещений. Таким образом, чем больше расстояние между зажимами, тем больше влияние на регистрируемые перемещения за счет этого фактора. Этот факт подтверждают данные, приведенные на рис. 5. Из сравнения деформирования образцов разной длины видно, что для образца длиной 22 и 16 мм максимальная разница в перемещениях при 140 ° С составила 9,67 мкм. Учитывая эти данные, можно дать количественную оценку эффективного значения КЛТР оснастки. Полученное значение а = 16,1 •W - ’ K ^{- 1} соответствует КЛТР ряда зарубежных и отечественных нержавеющих сталей а = (15 -17) •10 ^{- 6} K ^{- 1} [29; 30].

Анализ полученных экспериментальных данных (см. рис. 5, 6) показывает, что увеличение температуры сопровождается отрицательными перемещениями. Объяснить наблюдаемый эффект можно, основываясь на особенностях конструкции оснастки (см. рис. 2), в условиях эксперимента с контролируемой силой: при большем деформировании стационарно зафиксированной траверсы относительно меньшего по размерам нижнего подвижного плунжера, соблюдая заданные условия по постоянной силе натяжения образца, управляющий модуль DMA перемещает плунжер вверх вслед за деформирующейся траверсой. Именно на этом подвижном плунжере размещен оптический датчик перемещений.

Таким образом, полная деформация описанной системы еЛ р , фиксируемая в процессе эксперимента, состоит из суммы температурных деформаций образца ^ обр и осн

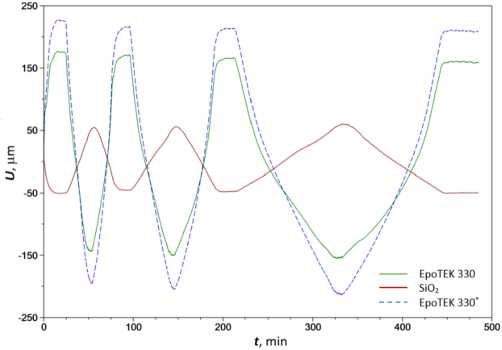
Рис. 7. Коррекция температурной деформации образца из полимера EPO-TEK-330 с учетом данных деформирования оснастки, полученных в эксперименте на образцах из кварцевого стекла

еи =е T +£ T .

обр обр осн .

То же самое будет справедливо и для перемещений

0 TT

Ur — U +U обр обр осн ^.

Fig. 7. Temperature dependence of strain for EPO-TEK-330 for different cooling/heating rate; sample thickness 36.7 microns

Зная КЛТР SiO 2 , а следовательно, и температурную деформацию образцов из чистого кварцевого стекла, можно из натурного эксперимента получить перемещение плунжера, обусловленное температурной деформацией оснастки (3):

SiO2

TT

SiO2 осн ;

T0 T u осн = u SiO2   u SiO2 ,

где иосн - перемещение плунжера; uSiO2 - перемещения, фиксируемые в процессе натурного эксперимента на об-„ „  „ „ т „ разцах из кварцевого стекла; иSiO2 - перемещения, рассчитанные по известным данным КЛТР для плавленого кремнезема.

Выразив из (2) u _о ^T _бр и подставляя (3) в (4), получим выражение для определения перемещений исследуемого образца, обусловленных его температурной деформацией, с учетом компенсации деформирования оснастки (5):

T0T uобр = uобр uосн ;                      (4)

u обр = u обр - u SiO 2 + u SiO 2 ■                 (5)

Учет поправки увеличит абсолютные значения перемещений и деформаций, а кривые, соответствующие нагреву и охлаждению, будут еще сильнее разнесены друг от друга по оси абсцисс.

С учетом деформации оснастки, полученной в эксперименте с пластинками из кварцевого стекла (см. рис. 5, 6), зависимости, представленные на рис. 3, 4, будут иметь следующий вид (рис. 7, 8).

Дифференцируя полученные зависимости по температуре, были получены температурные зависимости КЛТР исследуемых образцов для конкретных скоростей изменения температуры (рис. 9).

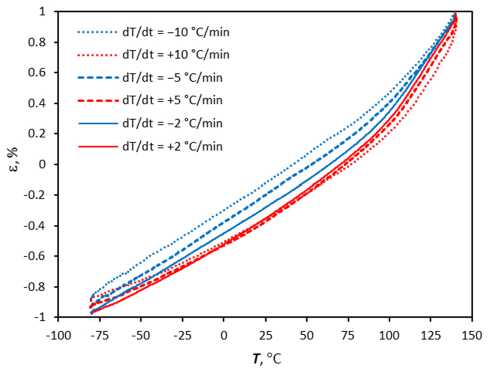
Рис. 8. Зависимость деформации от температуры для полимера EPO-TEK 330 для разных скоростей изменения температуры с учетом компенсации деформации оснастки

Fig. 8. Temperature dependence of deformation for EPO-TEK-330 polymer for different rates of temperature change, taking into account the compensation of deformation of the tooling

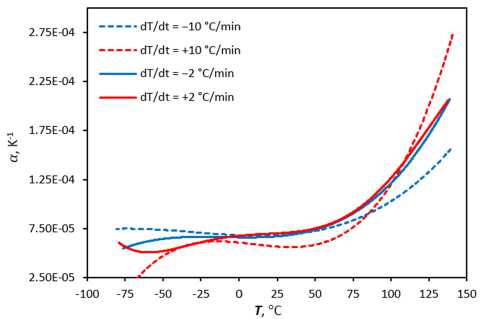
Рис. 9. Зависимость КЛТР от температуры полимера EPO-TEK-330 для разных скоростей изменения температуры

Fig. 9. The dependence of the CTE on the temperature of the EPO-TEK-330 for different cooling/heating rates

Полученные результаты более точно описывают деформационный отклик материала, чем предоставляемые производителем табличные значения (таблица). Анализ полученных результатов (см. рис. 8, 9) подтверждает, что температура и скорость ее изменения существенно влияют на деформационный отклик полимерных пленок [15], а отличие КЛТР при нагреве и охлаждении может достигать десятков процентов (см. рис. 9).

КЛТР по данным производителя [35]

CTE according to the manufacturer [35]

Марка полимера	T g , °C	T <  T g , °C-1	T >  T g , °C-1
EPO-TEK-330 (rev.3)	90	39 - 10-6	175 - 10-6
EPO-TEK-330 (2019)	90	65 - 10-6	162 - 10-6

Для достаточно широкого спектра прикладных задач, в частности в случаях с массивными образцами или при невысоких скоростях изменения температуры, различием КЛТР при нагреве и охлаждении можно пренебречь. В таком случае, получив средние значения перемещений в одном из циклов «нагрев – охлаждение» и построив аппроксимацию, выведем функциональную зависимость температурной деформации и КЛТР от температуры. Установленная зависимость будет близка по значениям к деформационному отклику материала при скорости изменения температуры около 0 °С/мин (рис. 10). Такой подход к оценке КЛТР аналогичен методике, приведенной в стандартах [31; 32].

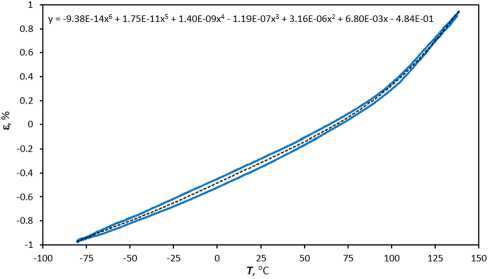
Рис. 10. Зависимость температурной деформации EPO-TEK-330 от температуры при скоростях ее изменения близких к 0 °С/мин

Fig. 10. The dependence of the temperature deformation of EPO-TEK-330 on temperature at rates of change close to 0 °C/min

2.    Верификация

Значительное внимание в работе было уделено верификации методики измерения КЛТР пленочных образцов. Для этого были выполнены натурные исследования на образцах из пищевой алюминиевой фольги, так как данные по температурному расширению алюминия хорошо известны и описаны в литературных источниках. Фольгу, как правило, изготавливают из первичного или технического алюминия марок А0, АД0, АД1 или из деформируемых сплавов АЖ1, АЖ0.8, потому что эти сплавы обладают высокой пластичностью. В рассматриваемом в рамках эксперимента диапазоне изменения температур 50... 150 °С КЛТР перечисленных выше марок алюминия составляет а = (24...25,6)-10-6 К-1 [18; 29; 33].

В соответствии с описанными процедурами были выполнены эксперименты на образцах из пищевой алюминиевой фольги и кварцевого стекла одинаковой длины в одних и тех же условиях. Образцы из алюминиевой фольги имели характерные размеры: длина 12…18 мм, ширина 6,25 мм, толщина 7…7,5 мкм. Образцы из кварцевого стекла шириной 3,01 мм, толщиной 0,558 мм, длину образца регулировали в соответствии с длиной образца из алюминиевой фольги от 12 до 18 мм.

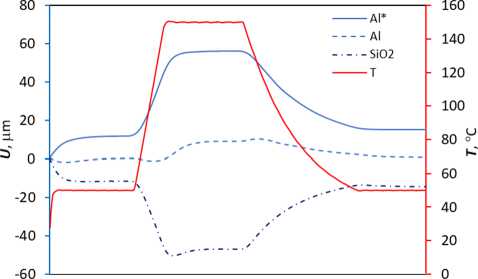
Все образцы нагревали со скоростью 5 ° С/мин с температуры 50 до 150 ° С и охлаждали естественным способом до 50 ° С. По аналогичной программе повторяли эксперимент на образце из кварцевого стекла той же длины для того, чтобы получить эталонную кривую, для компенсации температурной деформации оснастки. На рис. 10 приведены характерные зависимости температуры, перемещений для образцов из алюминиевой фольги u _A ⁰ _l ( t ) и из кварцевого стекла u _S ⁰ _{iO 2} ( t ) от времени и полученная с учетом компенсации кривая u Al ⁽ t ) = u Al ⁽ t ) - u SiO₂⁽ t ) + u SiO₂⁽ t ) .

0        50       100       150      200      250

t, min

Рис. 11. Определение истинной зависимости удлинения образца u^T _Al ( t ) (Al*) по полученным в эксперименте данным о деформировании оснастки u _S ⁰ _iO2 ( t ) (SiO 2 ) и алюминиевой фольги (Al)

Fig. 11. Determination of the true dependence of sample elongation (Al*) based on experimentally obtained data on the deformation of clamps (SiO2) and aluminum foil (Al)

Среднее значение рассчитанного по трем парам образцов КЛТР алюминиевой фольги было определено как a = 25,85 -10 ^{- 6} K ^{- 1} , что хорошо соответствует известным литературным источникам [18; 29; 33].

Также для верификации полученных данных (см. рис. 9) были сделаны образцы из эпоксидной смолы

EPO-TEK 330 в виде параллелепипеда с размерами 2,03×3,1×11,95 мм и выполнено исследование КЛТР на горизонтальном дилатометре TA DIL 802. Все полученные результаты, а также данные производителя приведены на рис. 12. Из данных, приведенных на рисунке, видно, что полученные результаты находятся в пределах, обозначенных производителем значений, и удовлетворительно согласуются с данными, полученными на дилатометре.

Таким образом, установлено, что полученные значения КЛТР соответствуют известными справочными данными для рассматриваемых материалов, а построенные зависимости КЛТР от температуры удовлетворительно согласуются с данными, полученными другими методами измерения. На основании представленных результатов можно утверждать, что описанная методика исследования деформационного отклика пленочных образцов на изменение температуры корректна и может быть использована для установления зависимости КЛТР от температуры.

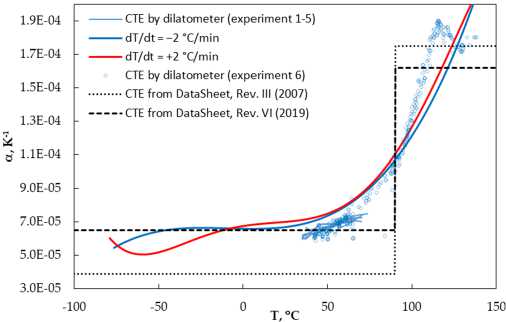
Рис. 12. Сравнение данных по КЛТР полимера EPO-TEK-330, полученных на ДМА TA Q800, дилатометре TA DIL 802 и от производителя

Fig. 12. Comparison of CTE data for EPO-TEK-330 obtained on a TA Q800 DMA, a TA DIL 802 dilatometer and from the manufacturer

В заключение была выполнена оценка однородности температурного поля по толщине рассматриваемых образцов. В соответствии с работой А.И. Пеховича и В.М. Жидких [34] осуществлена оценка равномерности температурных полей для всех рассматриваемых образцов с учетом свойств материалов, характерных размеров образцов, при разных скоростях изменения температур. Оценочный расчет выполнялся для неограниченной пластины с учетом ее симметрии, линейного изменения температуры на поверхности и отсутствия теплового потока на плоскости симметрии. Расчеты показали, что для рассматриваемых образцов из алюминиевой фольги, пластин из чистого кварцевого стекла, полимера EPO-TEK 330 отношение температуры в центре и на поверхности практически равно единице во всем диапазоне рассматриваемых температур при скоростях ее изменения от 0 до 50 ° С/мин.

3.    Рекомендации

В целях повышения точности измерений рекомендуется при проведении натурных испытаний использовать максимально возможную длину образцов, так как увеличение измеряемой базы повышает точность эксперимента.

В наиболее распространенных расчетных пакетах, таких, например, как ANSYS, Comsol, Abaqus и др., для учета КЛТР, зависящего от температуры, можно использовать аналитическое выражение, описывающее закон изменения термической деформации от температуры е Т ( T ) = f ( T ). Таким образом, полученные представленной методикой зависимости деформации от температуры хорошо ложатся в расчетные схемы без необходимости их дифференцирования по температуре.

Для корректного использования описанных функциональных зависимостей необходимо ввести в f ( T ) дополнительное слагаемое, обеспечивающее равенство е T ( T ₀) = 0 при температуре отсчета температурной деформации.

Особое внимание необходимо уделять корректному подбору усилия натяжения, которое, с одной стороны, должно обеспечить плоскопараллельность поверхностей пленки в течение всего эксперимента, а с другой – не будет приводить к неограниченной ползучести. В большинстве случаев для УФ-отверждаемых полимеров это сделать удается, потому что, как правило, при полимеризации в них под действием светового облучения формируются трехмерносшитые сетки [36], препятствующие развитию ползучести. При исследовании образцов из линейных полимеров, для которых при температурах выше температуры стеклования характерно развитие неограниченной ползучести даже при незначительных нагрузках, необходимо так подобрать температурный диапазон, чтобы в верхней его части образец под растягивающей нагрузкой находился в равновесном состоянии. Для ряда аморфных полимеров при температурах выше температуры стеклования описанная методика может быть неприменима в полной мере, что в каждом конкретном случае можно проверить в экспериментах на ползучесть, варьируя нагрузку и температуру.

Заключение

В результате выполненного исследования предложен подход к исследованию деформационного отклика пленочных образцов из полимерных стеклующихся материалов на температурное воздействие в различных режимах. Преимущества разработанного подхода в значительной степени обусловлены тем, что в качестве образцов использованы тонкие пленки, в которых удается сформировать достаточно однородное температурное поле в широком диапазоне скоростей изменения температуры. Сформулированная методика постановки натурных экспериментов и предложенные рекомендации для измерения коэффициента температурного расширения пленочных образцов позволяют также получить функциональные зависимости КЛТР от температуры и скорости ее изменения.

Преимуществом предлагаемого подхода является также то, что на одном и том же образце можно собирать данные и для анализа температурного расширения, и для определения вязкоупругих характеристик.