Об одном методе описания турбулентных течений

В свое время еще Прандтль обратил внимание на то, что имеется физическая аналогия между разреженным газом и турбулентной жидкостью. В качестве обобщения применения кинетических моделей в работе О.М. Белоцерковского, В.Е. Яницкого [1] была рассмотрена кинетическая модель описания турбулентности при помощи функции распре- деления, в которой аргументом является не молекулярная скорость У, как в разреженном газе У = У (t, г, У), а v - пульсации скорости жидкой частицы У = У (t, ж, v). Тогда уравнение для функции распределения У = У (t, ж, v) описывается уравнением Онуфриева-Лундгрена [2, 3] для одномерного случая

дУ ₊ дУ dt ^Сдж

-

1 Э      У м - У

VE ) =-------,

2т 1 dt            т ₂

здесь v = с — и - пульсационная скорость, ап = ( с ) - средняя скорость потока. Функция

У м = [ ... Г [— . ]

является плотностью вероятностей нормального закона распределения пульсаций скорости, q ² = (с² + v ² + v2^ - удвоенное среднее значение удельной кинетической энергии этих пульсаций Е.

Уравнение (1) очень похоже на модельное кинетическое уравнение Крука [4]:

эу ЭУ _      п

Эй ^{+ с}эЖ =^{7 ( У} 0 ^{— У} ) •

Форма уравнения для сплошносредных пульсаций (1), аналогичная кинетическому релаксационному уравнению (3), подкупает тем, что открывает возможность использовать аппарат методом Монте–Карло, хорошо развитый в динамике разреженных газов [5–7].

• 2.    Постановка задачи о диссипации турбулентных пятен

  • 2.1.    Жидкостная модель описания турбулентности

• 2.2.    Постановка эксперимента Наудашера [9]

Итак, в предлагаемой модели Белоцерковского–Яницкого каждая жидкая частица обладает некоторым набором качеств - координатами ж и скоростями пульсаций v (см. табл. 1). Для этой функции распределения предлагается модель кинетического уравнения, аналогичная модельному уравнению в динамике разреженных газов [5].

Таблица1

Сравнительное описание среды функцией распределения для задач динамики разреженного газа и турбулентности

Динамика разреженного газа	Турбулентность
Частицы
Модель молекулы г - координаты молекул £ - скорости молекул	Модель жидкого объёма ж - координаты частиц ж - скорости пульсаций
Функция распределения
/ = / (t,r,£) У / d£ = Р — плотность	/ = / (t,ж,У) J" / dv = 1 - нормировка
Моменты
4 У £/ d£ = и - скорость газа (€ — и) - тепловая скорость	J v/dv = и - средняя скорость течения (v - и) - скорость пульсации

Для описания турбулентности используется релаксационное кинетическое уравнение Онуфриева–Лундгрена [2, 3].

Задача составилась следующим образом. Задача возникла из рассмотрения безымпульс-ного следа за генератором пульсаций диаметра D, размещенного в потоке с постоянной скоростью U o (см. рис. 1). Безымпульсность, т.е. отсутствие в среднем по течению переноса массы вдоль оси следа Ож, позволяет на достаточном удалении от источника пренебречь неоднородностью профиля средней скорости и напряжениями трения. В этой области пространственное распределение энергии q ² является автомодельным, развитие турбулентного следа происходит так, как будто он инициирован точечным источником пульсаций, размещенным в потоке со скоростью U o , и при расчете полей можно принять, что t = ж/U o на расстояниях ж > 4D. Таким образом, в терминах соответствующей временной переменной ж = ж/U o при времени t >  t o = 4D/U o измеряемая функция q ² (t,y,z) приобретает гауссовский вид:

q ² (t, г) = q ² (t, у, z) = q^ (t) exp [- 0.69г 2 /г² (t) ] .

г = ( у ² + z ² ) 1 ^{/ 2} , q ² (t,r _q )= q^ (t) /2.

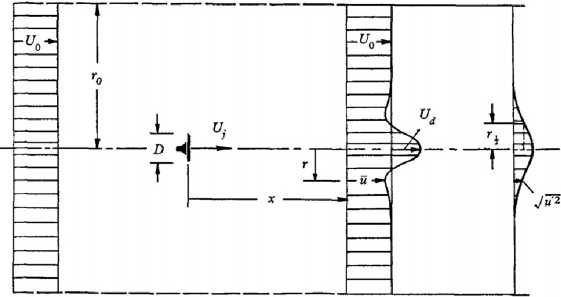
Рис. 1. Установка эксперимента Наудашера, г ₀ = 5D

Энергия q^ (t) в центре пятна и его характерный радиус аппроксимируются следующими зависимостями:

2 _    2 Л, t - t o V¹           ( t - t o V²

qm (t) = qo I1+ ?i ~,гу (t) = ro l1 +           , где m = 1.58, П2 = 0.35, то = 2D/Uo для 5OD/Uo < t < 13OD/Uo, а для to 6 t 6 5OD/Uo показатели и равны 1.80 и 0.25 соответственно. Характерным радиусом пятна считается расстояние от центра, на котором энергия уменьшается вдвое по сравнению с энергией в центре пятна.

Для численного моделирования рассматривается зародыш турбулентности в виде некоего пятна (см. рис. 2), затем рассматривается эволюция этого пятна во времени в соответствии с жидкостной моделью.

Рис. 2. Диссипация турбулентного пятна (начальная область)

• 3.    Метод решения

  В качестве начальных функций распределения f (у, z, с) принималась плотность нормального закона для распределения вероятностей мгновенных значений гидродинамической скорости, то есть

  
  

^{f o (г},^с) = [ 2^5 2 (Г) ] exp [ ^—2#) ] '

где q O (г) = Q 0 ^exP [—О.69г 2 /г0]. Соответственно физическим процессам схема моделирования эволюции модели на малом временном интервале At представляет собой последовательность трех этапов.

Этап I . Основное уравнение (перенос турбулентности):

df . df _n dt + СӘх описывает движение системы из жидкостных частиц, не взаимодействующих между собой.

Уравнения движения каждой частицы имеют следующий вид:

dr

— Ci . dt

Тогда координаты каждой частицы во времени t + At определяются уравнением г (t + At) = г (t) + с (t) At, где г = 1, 2,..., N.

Этап II . Моделирует диссипацию турбулентной энергии: каждая подсистема частиц в ячейках эволюционирует согласно основному уравнению процесса.

9f dt

— ^2^f) =0. дс \2т і

На этом этапе меняются лишь скорости всех N частиц, находящихся в данной ячейке, по следующему закону:

^{— —} 2 7 1 ^V-’ ^{т — 1} 2’ '"’ ^N’

_ !р\ (!) /Ч(і) _ х VN г(1)

^и г ^{— с}г \ ^c > N ’ \ ^c > N ^— Мм =і ^c j ■

Используем зависимости ті (q2^ — т0 (q2/q2) и q2 — q0 (1 + 7^/т0) 1/71, подставляем в формулу (3). После интегрирования получаем скорости каждой частицы для этапа дисси- пации энергии:

c ⁽²⁾ — < c > N ) +

X - < e > N ^> (1+ і V-    ' 2 - ¹ ■

Здесь верхние индексы указывают номер этапа, на котором получены данные величины.

Этап III (перераспределение пульсаций по степеням свободы). Основным уравнением является пространственно однородное уравнение БГК:

df _— f м - /

Qt      T2

которое моделируется в каждой ячейке. Строго говоря, пульсационные скорости каждой из частиц в ячейке в соответствии с (4) должны вычисляться так:

(3)        (2)     ,             \

V ^— V ' X ⁺ (I ^— X) У

Здесь x — случайная величина, принимающая значение 0 или 1 с вероятностью exp ( — t/T 2 ) и 1 — exp(—t/T 2 ) соответственно, ту - случайная величина, распределенная с плотностью вероятностей /м. Однако в такой ситуации вычислительный алгоритм (5) не сохраняет энергию всей подсистемы. Случайные колебания <^v² ^ в среднем имеют порядок величины N ^{-і / 2} .

Для реализации данного этапа имитации в [9] был предложен метод, точно сохраняющий энергию Е — с ² + ■ ■■ + c N и импульс Р — с і + ■ ■■ + c n всей системы и представляющий собой следующее преобразование:

С(3) — С(2)x + (1 — X) ТС(2), С — {сі’ ■■■’ cn} ’ здесь Т - такая случайная матрица вращения 3N-мерного вектора С, что точка ТС равновероятно распределена на гиперсфере постоянных энергий Е и импульса Р системы из N (3)

частиц в данной ячейке. Каждая пульсационная скорость V - ', получаемая таким образом, асимптотически (при N >>  1) эквивалентна величине v ⁽³⁾ в формуле (5), причем скорость сходимости имеет порядок величины N ^-1 .

Практически этот этап реализуется так. Разыгрывается 3(N — 1) независимых случай ных значений уі, 72, У3’■■■’У3N-5, 73N-4, 73N-3, величины у, распределенной нормально с дисперсией с2 — 1 и нулевым средним. Вычисляются величины £- (г — 1, ■■■, 3N — 3) по следующей формуле:

3 N - 3

р ^— У г ^ €/ ^2 ^T| j j ■

j =1

Они являются координатами 3 (N — 1)-мерной точки { ^ і , ■■■, z n - і } , равномерно распределенной на гиперсфере радиуса R — V ? с центром в нуле. Полагаем Z n — Р/VN и переходим от компонент { ^ і , ■■■, z n - і } к компонентам { с і , ■■■, c n - і } с помощью преобразования вращения с - — ^ j ^ T j- Z j , где T n- — 1/VN . На этом реализация шага 3 заканчивается. Следующая лемма [9] формулирует экономичный алгоритм преобразования С — Т Z , где Z — { Z 1 , ■■■’Z n } ■

Лемма. Обратное преобразование С = Т Z может быть реализовано следующей последовательностью из преобразований вращений

С п

I N-п

N N + 1 -

— ^Zn ⁺ п

VN + 1 - п

( ^{( п -1) C} N

п = 1,...,N - 1,

сУ =__ ,   ¹

^N     VN +1 -п

/ ^{N -п}  _с ( п - 1)

\ N + 1 - п ^N

п = 1,...,N - 1,

(0)           ( N - 1)

C N = Z N , C N    = C N .

При реализации данного алгоритма были приняты следующие параметры задачи: 7 1 = 0.63, 7 2 = 0.8, L ⁰ = L ⁰ = 0.14, этому соответствует значение релаксационных параметров: т ⁰ = т ⁰ = 1.31.

• 4.    Численные расчёты

  • 4.1.    Эволюция турбулентного пятна

    В данном расчёте размеры области разбивались на 41 х 41 ячеек. Общее количество частиц – 168 100 (значит, что в начальном времени среднее число молекул в каждой ячейке равно 100). Время эксперимента было 40 с. Шаг по времени для разных реализаций равнялся 0.085 , 0.05 , 0.425 , 0.0275 с. Начальная удельная энергия турбулентных пульсаций в центре пятна q 0 для разных реализаций равнялась 0.0204 и 0.0104 м ² /с ² , а характерный радиус г 0 равнялся 0.612 м. q 0 и г 2 выбирались таким образом, чтобы на временном интервале t 6 20 были малы эффекты влияния градиента давления V P и конечный размер расчетной области. В качестве результатов представлены графики зависимости энергии в центре пятна от времени. Для получения гладкой картины достаточно порядка 100 реализаций.

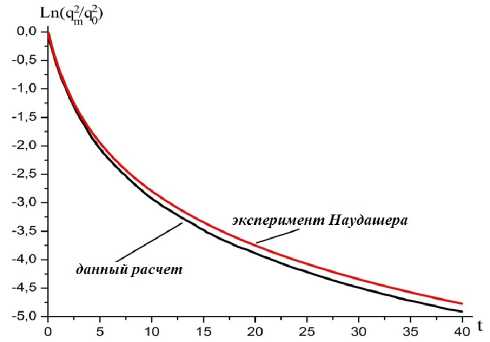
Рис. 3. Зависимость энергии в центре пятна к его начальному значению от времени

Была исследована зависимость удельной энергии флуктуаций в центре «турбулентного пятна» от времени. Так, на рис. 3 представлена зависимость логарифма отношения энергии в центре к его начальному значению от времени.

На рис. 4 и рис. 5 показаны отнормированные кривые удельной энергии в момент времени t = 0 и t = 34 с.

Как видно из графиков, происходит «расползание» пятна вдоль радиуса. Это обусловлено смещением более быстрых частиц из центра к краям области.

На рис. 6 приведены распределение удельной энергии пульсаций, усредненные вдоль радиуса из центра области в последовательные моменты времени с шагом At = 10.

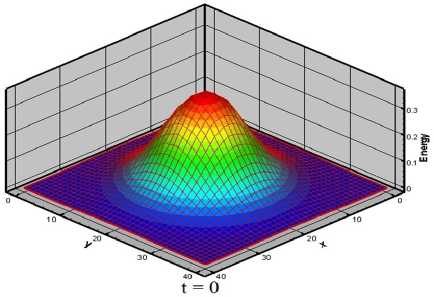
Рис. 4. Пятно в начальный момент времени t = 0

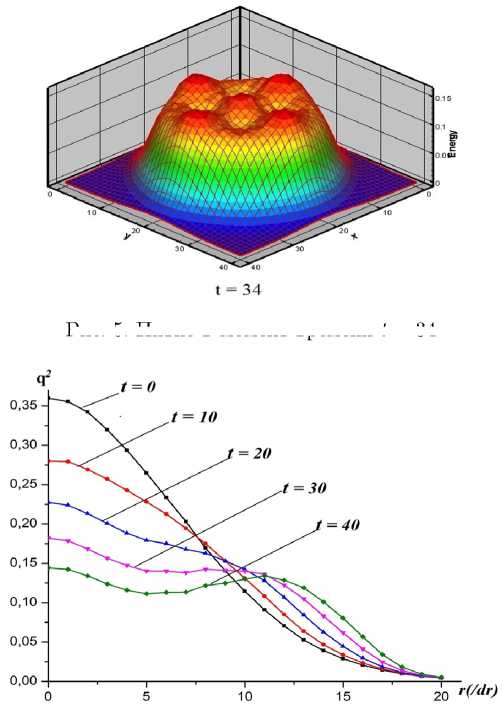
Рис. 5. Пятно в момент времени t = 34

Рис. 6. Распределение удельной энергии пульсации по радиусу пятна в определенные моменты времени

В расчётах также были получены распределения энергии по радиусу пятна в разные моменты времени t = 4.25, 8.5,17 с (см. рис. 7). Полученные расчеты сравнились с экспериментальными данными Наудашера [10]:

-2 q f f- т А q =    = / т =     , qm     V Tm / где т - относительный радиус. Физический эксперимент [10] для автомодельной кривой / (т) дает следующую функцию:

/ (т) = exp (- 0.69т ² ) .

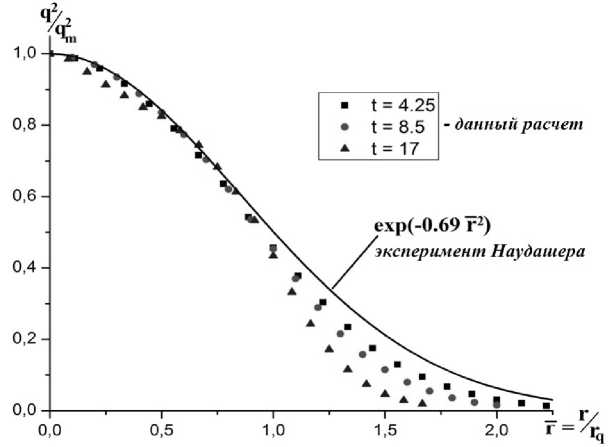
Рис. 7. Распределение энергии по относительному радиусу пятна

• 4.2.    Интерференция турбулентных пятен

  В рамках выше описанной модели Белоцерковского–Яницкого–Онуфриева решалась задача о взаимодействии эволюционирующих турбулентных пятен. Ввиду большого вычислительного объёма задачи моделирование проводилось на многопроцессорной системе МВС–1000. Суть алгоритма для всех вариантов методов Монте–Карло довольно проста. На всех процессорах независимо друг от друга организовывается статистическое моделирование. По истечению времени установления решение усредняется по всем процессорам.

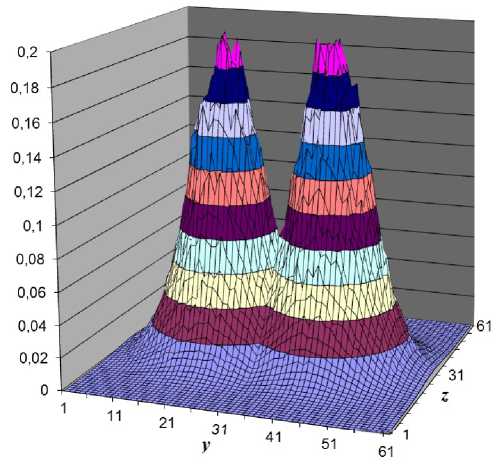
Рис. 8. Распределение удельной энергии взаимодействующих пятен при t = 0 с

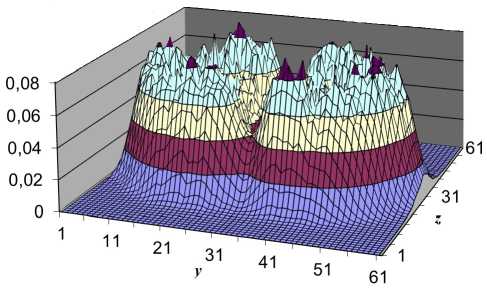
Рис. 9. Распределение удельной энергии взаимодействующих пятен при t = 40 с

Размеры области [у х z] разбивались на 61 х 61 ячеек. Шаг по времени составлял 0.085. Остальные параметры такие же, как описаны выше для задачи о диссипации турбулентного пятна. На рис. 8 показана удельная энергия двух взаимодействующих пятен в начальный момент времени t = 0 с. На рис. 9 получено распределение удельной энергии взаимодействующих пятен в момент времени t = 40 с. Из графиков видно, что здесь так же происходит «расползание» пятен вдоль радиуса. Это обусловлено смещением более быстрых частиц из центра к краям области и перераспределением энергии на границах между пятен.

На рис. 10 показаны распределения удельной энергии взаимодействующих пятен по времени t = 0, 20,40 с по оси у.

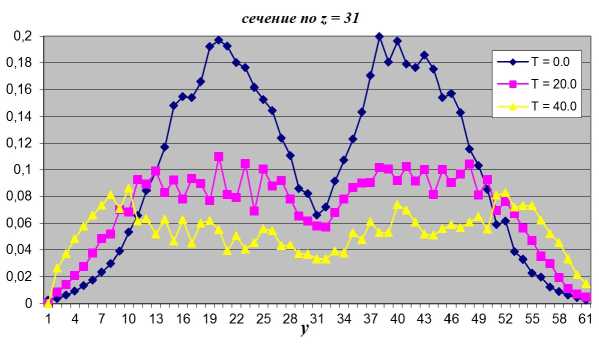
Рис. 10. Взаимодействие двух турбулентных пятен (распределение энергий)

• 5.    Заключение

Представлен метод статистического моделирования свободной турбулентности. Математической моделью является кинетическое уравнение Онуфриева–Лундгрена для функции распределения скоростей пульсаций. Для решения уравнения использован хорошо зарекомендовавший себя в разреженном газе метод прямого статистического моделирования (Монте-Карло). Решены задачи о диссипации турбулентного пятна (проблему можно интерпретировать как дальний след в несжимаемой жидкости) и интерференции двух пятен.