Об одном методе расчета изгибных и сдвиговых колебаний пористого пьезоэлемента в низкочастотной области
Автор: Соловьев А.Н., Чебаненко В.А., Оганесян П.А., Фоменко Е.И.
Журнал: Advanced Engineering Research (Rostov-on-Don) @vestnik-donstu
Рубрика: Механика
Статья в выпуске: 2 т.24, 2024 года.
Бесплатный доступ
Введение. Устройства сбора и накопления энергии из внешней среды представляют собой маломощные источники электрической энергии, которые активно используются, в том числе в автономных приборах мониторинга поврежденного состояния различных конструкций. Рабочим элементом этих устройств является пьезоэлектрический генератор (ПЭГ) - преобразователь механической энергии в электрическую. Конструирование ПЭГ связано с предварительным построением их математических и компьютерных моделей, с помощью которых производится расчет и оптимизация конструкций. Одним из способов моделирования и расчета ПЭГ является разработка приближенных методов расчета на основе прикладных теорий. В литературе известны и ранее разработаны прикладные теории расчета изгибных колебаний многослойных пьезоактивных пластин. Однако информации об изгибно-сдвиговых колебаниях, как инструменте повышения эффективности инженерных расчетов описанных конструкций, в научной литературе недостаточно. Целью настоящей работы являлась разработка прикладного метода расчета изгибных и сдвиговых колебаний пьезокерамических пластин, в том числе пористых.Материалы и методы. В качестве пьезоактивного материала пластины используется пьезокерамика PZT-4, в том числе пористая. При использовании пористой керамики жесткость конструкции уменьшается в большей степени, чем пьезомодули, что позволяет получить более эффективный ПЭГ при механическом воздействии. Математическая постановка осуществлена в рамках линейной теории электроупругости при поляризации пластины по толщине. Боковые стороны пластины электродированы, правая сторона закреплена, а на левой задан гладкий контакт в вертикальной стенке. Установившиеся колебания пластины вызываются давлением на лицевые поверхности пластины или разностью электрических потенциалов на электродах. Для расчета характеристик ПЭГ в работе предлагается прикладная теория, основанная на гипотезах о распределении характеристик напряженно-деформированного состояния и электрического поля.Результаты исследования. Рассмотрены поперечные колебания пьезокерамической пластины в низкочастотной области (ниже первого изгибно-сдвигового резонанса). В силу того, что математическая постановка рассмотрена в рамках линейной теории упругости, задача разделилась на сумму двух. В первой учитывалось механическое воздействие: на лицевые поверхности пластины действует распределенная нагрузка и поперечная сила на левом конце, а потенциалы на электродах равны нулю. Во второй задаче механические нагрузки отсутствовали, но задавалась разность потенциалов на электродах. На основе гипотез о распределении деформаций, механических напряжений и электрического потенциала обе задачи были сведены к системе обыкновенных дифференциальных уравнений и граничных условий. Сравнение с результатами расчетов методом конечных элементов в пакете ACELAN показали адекватность предложенной прикладной теории в низкочастотной области. Обсуждение и заключение. Поскольку постановка задачи рассматривалась в линейной теории электроупругости и изучалась низкочастотная область, в работе удалось задачу об изгибных и сдвиговых колебаниях пластины из пористой пьезокерамики разделить на две: изгибную - с механическим воздействием при нулевых потенциалах и сдвиговую - при задании разности потенциалов и нулевом механическом воздействии. Использованы соответствующие гипотезы об изгибе и сдвиге, построены две системы обыкновенных дифференциальных уравнений и граничных условий, которые решаются аналитически без использования «тяжелых» конечно-элементных пакетов. Для сравнения результатов и подтверждения адекватности предложенного метода проведено конечно-элементное моделирование таких задач в специализированном пакете ACELAN. Это сравнение показало, что ошибка в определении смещений и электрического потенциала при использовании этого подхода, в случае задания механических нагрузок и разности потенциалов, не превышает 6 %. Разработанный в статье метод может быть применен при проектировании пьезоэлектрических генераторов накопления энергии в низкочастотной области.
Устройство сбора энергии, пьезоэлектрический генератор, пористая керамика, изгиб пластины, сдвиг пластины, прикладная теория
Короткий адрес: https://sciup.org/142241586
IDR: 142241586 | УДК: 534.1 | DOI: 10.23947/2687-1653-2024-24-2-148-158
Текст научной статьи Об одном методе расчета изгибных и сдвиговых колебаний пористого пьезоэлемента в низкочастотной области
Original Theoretical Research
On a Method for Calculating Bending and Shear Vibrations of a Porous Piezoelementin the Low-Frequency Region
Arkadiy N. Soloviev1,2, 3 © И , Valery A. Chebanenko2,3,4 , Pavel A. Oganesyan 2 © , Elizaveta I. Fomenko2 ©
-
1 Crimean Engineering and Pedagogical University named after Fevzi Yakubov, Simferopol, Republic of Crimea
-
2 Southern Federal University, Rostov-on-Don, Russian Federation
-
3 Don State Technical University, Rostov-on-Don, Russian Federation
-
4 Southern Research Center, Russian Academy of Sciences, Rostov-on-Don, Russian Federation
Introduction . Devices for collecting and storing energy from the external environment are low-power sources of electric energy that are actively used. The autonomous devices for monitoring the damaged condition of various structures include them as well. The working element of these devices is a piezoelectric generator (PEG) — a converter of mechanical energy into electrical energy. The design of PEG is associated with the preliminary construction of their mathematical and computer models, with the help of which the calculation and optimization of structures is carried out. One of the ways to model and calculate PEG is to develop approximate calculation methods based on applied theories. The applied theories for calculating bending vibrations of multilayer piezoactive plates are known and previously developed in the literature. However, in the scientific literature there is not enough information about bending and shear vibrations as a tool for improving the efficiency of engineering calculations of the described structures. The objective of this work was to develop an applied method for calculating bending and shear vibrations of piezoceramic plates, including porous ones.
Materials and Methods . Piezoceramics PZT-4, including porous ones, were used as the piezoactive material of the plate. When using porous ceramics, the rigidity of the structure decreased to a greater extent than the piezoelectric modules, which made it possible to obtain a more effective PEG under mechanical action. The mathematical formulation was carried out within the framework of the linear theory of electroelasticity with plate polarization in thickness. The sides of the plate were electrodated, the right side was fixed, and a smooth contact in the vertical wall was set on the left side. Steady-state vibrations of the plate were caused by pressure on the front surfaces of the plate or the difference in electrical potentials at the electrodes. To calculate the characteristics of PEG, the authors proposed an applied theory based on hypotheses about the distribution of characteristics of the stress-strain state and the electric field.
Механика
Results. Transverse vibrations of a piezoceramic plate in the low-frequency region (below the first bending-shear resonance) were studied. Due to the fact that the mathematical formulation was considered within the framework of the linear theory of elasticity, the problem was divided into the sum of two. The first one took into account the mechanical effect: a distributed load and a transverse force at the left end acted on the front surfaces of the plate, and the potentials at the electrodes were zero. In the second task, there were no mechanical loads, but the potential difference was set at the electrodes. Based on hypotheses about the distribution of deformations, mechanical stresses and electric potential, both problems were reduced to a system of ordinary differential equations and boundary conditions. Comparison with the results of calculations by the finite element method in the ACELAN package showed the adequacy of the proposed applied theory in the low-frequency region.
Discussion and Conclusion . Since the formulation of the problem was considered in the linear theory of electroelasticity, and the low-frequency region was studied, the work succeeded in dividing the problem of bending-shear vibrations of a porous piezoceramic plate into two: bending — with mechanical action at zero potentials, and shear — when setting the potential difference and zero mechanical action. The corresponding hypotheses about bending and shear were used. Two systems of ordinary differential equations and boundary conditions, which were solved analytically without the use of “heavy” finite element packages, were constructed. To compare the results and confirm the adequacy of the proposed method, the finite element modeling of such tasks was carried out in a specialized ACELAN package. The comparison showed that the error in determining displacements and electric potential when using this approach, in the case of setting mechanical loads and potential differences, did not exceed 6%. The method developed in the paper can be applied in the design of piezoelectric generators for energy storage in the low-frequency region.
Acknowledgements. The authors would like to thank the Editorial board of the journal and the reviewers for their attentive attitude to the article .
Funding Information. The research was done at the Southern Federal University with the financial support from the Russian Science Foundation (grant no. 22–11–00302).
Введение. Пьезоэлектрические генераторы (ПЭГ) используются для преобразования механической энергии в электрическую с последующим ее накоплением. Одна из областей применения ПЭГ — создание маломощных автономных возобновляемых источников электрической энергии. Рабочим элементом ПЭГ является пьезокерамический элемент определенной формы. Форма и тип деформации этого элемента определяют пьезомодуль, который характеризует преобразование механической энергии деформации в электрическую. Так пьезомодуль d 33 связан с растяжением-сжатием вдоль оси поляризации, d 31 — с такой же деформацией в поперечном направлении к этой оси, d 15 — со сдвигом. Использование пористой керамики позволяет создавать более эффективные ПЭГ. Это связано с тем, что модули упругости пористой керамики с ростом пористости убывают значительно сильнее, чем пьезомодули. Таким образом при одной и той же механической нагрузке амплитуда деформации у пористой керамики будет больше, следовательно, выходной электрический потенциал также больше.
Расчет ПЭГ может быть произведен методом конечных элементов, реализованном в пакетах ANSYS, ACELAN, COMSOL и других. Для пьезоэлементов, один или два размера которых значительно меньше других (пластины, стержни), могут быть построены прикладные теории расчета на основе гипотез о распределении механического и электрического полей. Без применения «тяжелых» конечно-элементных пакетов прикладные теории позволяют моделировать различные устройств на основе пьезоактивных материалов. В качестве таких материалов рассматривались пьезоэлектрические, пьезомагнитные и композиционные пьезомагнитоэлектрические. Построение этих теорий основано на принятии гипотез о распределении механических, электрических и магнитных полей. Эти гипотезы связаны с характером колебаний упругих и пьезоактивных элементов ПЭГ. Наиболее распространенными конструкциями являются активные и полупассивные биморфы на основе многослойных пластин, поляризованные по толщине с электродами на лицевых поверхностях, совершающие поперечные изгибные колебания. Исследованию устройств со сдвиговой деформацией пьезоэлементов посвящен ряд работ. Электрическая модель с пьезоэлектрическими определяющими уравнениями режима d15 и модель с одной степенью свободы объединены для описания характеристик сбора энергии пьезоэлектрического кантилевера в сдвиговом режиме в работе [1]. Предлагаемая модель используется для моделирования частотной зависимости выходного пикового напряжения и мощности. Результаты показывают хорошее совпадение с экспериментом и конечно-элементным расчетом в ANSYS. В работе [2] разработан пьезоэлектрический преобразователь энергии сдвигового режима для использования энергии потока воды под давлением. Он преобразует энергию потока в электрическую энергию путем пьезоэлектрического преобразования с колебанием пьезоэлектрической пленки. Разработана модель конечных элементов для оценки генерируемого напряжения пьезоэлектрической пленки, которая хорошо согласуется с проведенным натурным экспериментом. Одномерная полностью связанная модель колебания балки на основе гипотез типа Тимошенко, которая предоставляет единую общую основу для анализа энергии в режиме сдвига и изгиба, представлена в работе [3]. В работе [4] изучается влияние неоднородности свойств пластины при сдвиговых и крутильных колебаниях ее центральной части. В экспериментальной работе [5] был представлен многослойно-цилиндрический пьезоэлектрический сдвиговый актуатор (MCPSA), работающий в режиме сдвига d15, для прецизионного срабатывания при большой механической нагрузке. Актуатор был изготовлен из пьезоэлектрических керамических колец Pb(Zr,Ti)O3 (PZT-51), которые были концентрически собраны вместе в электрически параллельном соединении с попеременно положительной и отрицательной поляризацией в осевом направлении. В работе [6] создан метаматериал из идентичных элементарных ячеек, спроектирован и изготовлен искусственный прототип устройства с характерными узорчатыми электродами и расположенными в ряд пьезокерамическими субъединицами, который, как доказано, идеально генерирует синтетическую деформацию сдвига грани. При том же напряжении возбуждения наблюдается усиление смещения сдвигового типа более чем на порядок, по сравнению с предыдущими объемными элементами в режиме d15. В статической постановке в работе [7] теоретически установлено поле электромеханической связи в сдвигово-изгибающем режиме для кольцеобразной пьезоэлектрической пластины. В соответствии с классической теорией упругих пластин малого изгиба и пьезоэлектрическими определяющими уравнениями было достигнуто аналитическое решение изгибной деформации пьезоактюатора под действием электрического поля и концентрированной или равномерно распределенной механической нагрузки. Механизм создания изгибной деформации объясняется осесимметричной сдвиговой деформацией, которая дополнительно вызывает изгибную деформацию одной пьезоэлектрической пластины в форме кольца. Этот механизм существенно отличается от механизма пьезоэлектрических биморфных или уни-морфных приводов, о которых сообщалось ранее. Проведена оптимизация конструкции кольцеобразного пьезоактуатора. В работе [8] на основе одномерной модели строится функция отклика датчика на основе сдвиговых резонаторов (срезы кварца) объемной акустической волны, которые перспективны для поточных измерений вязкости жидкости, например, в промышленных процессах. В работе [9] с помощью метода конечных элементов исследовался пьезоэлектрический преобразователь управления высотой полета с использованием деформации модели сдвига. В [10] теория функционально-градиентной пластины с четырьмя неизвестными сдвиговой деформации применяется для выражения компоненты смещения. Распределение электрического потенциала представляет собой линейную функцию по толщине. Пластина находится под механической нагрузкой и электрическим напряжением. Основные уравнения и граничные условия выводятся с использованием принципа виртуальной работы. Проведен анализ напряжений и деформаций от параметров конструкции. Электромеханический анализ потери устойчивости пьезоэлектрической нанопластины при сдвиге с использованием модифицированной теории парных напряжений с различными граничными условиями изучался в работе [11]. Чтобы учесть электрические эффекты, к пьезоэлектрической нанопластине прикладывали внешнее электрическое напряжение. Была использована упрощенная теория сдвиговой деформации первого порядка. Основные дифференциальные уравнения были получены с использованием принципа Гамильтона и нелинейных деформаций Фон-Кармана. В итоге результаты показали, что влияние внешнего электрического напряжения на критическую сдвиговую нагрузку, возникающую на пьезоэлектрической нанопластине, незначительно. В работе [12] с помощью комбинации двух классических подходов моделирования нелинейного поведения пьезоэлектрических материалов исследуется пьезоэлектрический привод сдвигового типа для атомно-силового микроскопа. В частности, новизна предлагаемого метода состоит в том, что он сочетает в себе два источника нелинейности полезависимой модели Мюллера и Чжана с частотно-зависимой моделью Дамьяновича. Численные результаты, полученные с помощью метода конечных элементов (МКЭ), сравниваются с экспериментом.
Менее исследованы в научной литературе колебания, в которых кроме изгиба присутствует сдвиг, т.е. «рабочим» является пьезомодуль d 15 , значение которого убывает с увеличением пористости, но в меньшей степени, чем упругие модули. Последнее обстоятельство позволяет построить эффективное устройство преобразования энергии. Поэтому разработка прикладной теории расчета ПЭГ с использованием пористой пьезокерамики на основе упрощенных моделей без использования «тяжелых» конечно-элементных пакетов представляется весьма актуальной задачей. Целью настоящей работы явилось построение прикладного метода расчета для установившихся поперечных колебаний в низкочастотной области пористой пьезокерамической пластины, характеризующиеся как сдвигом, так и изгибом.
Механика
Материалы и методы. Исследуемый ПЭГ представляет собой пьезокерамическую пластину (длина l , толщина h ), поляризованную по толщине, консольно-закрепленную по правой боковой стороне, левая боковая сторона прикреплена к инерционной массе, которая совершает вертикальные колебания и закреплена в горизонтальном направлении. Электроды расположены на боковых сторонах пластины, поэтому при разности потенциалов на них и отсутствии механической нагрузки, основной деформацией в низкочастотной области является сдвиг. Рассматриваются колебания, частота которых меньше частоты первого резонанса.
Математическая постановка задачи
Математическая постановка задачи описывается системой дифференциальных уравнений [13] и соответствующими граничными условиями.
ppkU + a djpjU-V-о = fj V-D = 0
о = c EE •( £ + P dj £ ) — e T - E E = -V^
D + g d D = e j •( £ + g d £ ) + э S - E £ = ( V u + V u T ) / 2
При рассмотрении пористой керамики связности 3–0 в уравнениях (1) используются эффективные физические константы, определенные с помощью пакета ACELAN-COMPOS [14] . Эти эффективные свойства на основе представительных объемов (рис. 1) получены в работе [15] и представлены в таблице 1.
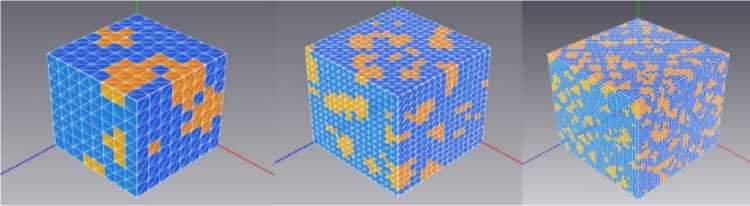
Рис. 1. Представительные объемы в пакете ACELAN-COMPOS [14]
Таблица 1
Эффективные свойства пористой керамики
|
% пористости |
0 |
10 |
20 |
30 |
40 |
50 |
60 |
70 |
80 |
|
P , kg/m3 |
7 500 |
6 750 |
6 000 |
5 250 |
4 500 |
3 750 |
3 000 |
2 250 |
1 500 |
|
c 1 E 1 eff, 1010 , N/m2 |
13,90 |
11,56 |
9,25 |
6,85 |
5,05 |
3,34 |
2,07 |
1,26 |
0,68 |
|
c 1 E 2 eff, 1010 , N/m2 |
7,78 |
6,15 |
4,66 |
3,14 |
2,10 |
1,16 |
0,62 |
0,28 |
0,13 |
|
c 1 E 3 eff, 1010 , N/m2 |
7,43 |
5,82 |
4,25 |
2,82 |
1,87 |
1,06 |
0,52 |
0,24 |
0,10 |
|
c 3 E 3 eff, 1010 , N/m2 |
11,50 |
9,53 |
7,23 |
5,42 |
3,91 |
2,72 |
1,63 |
0,91 |
0,47 |
|
c 4 E 4 eff, 1010 , N/m2 |
2,56 |
2,23 |
1,83 |
1,44 |
1,10 |
0,74 |
0,44 |
0,23 |
0,10 |
|
e 3e3ff , C/m2 |
15,10 |
13,38 |
11,37 |
9,59 |
7,68 |
5,93 |
3,93 |
2,30 |
1,25 |
|
e 3e1ff , C/m2 |
–5,20 |
–4,23 |
–3,14 |
–2,07 |
–1,32 |
–0,75 |
–0,43 |
–0,21 |
–0,10 |
|
e 3e1ff , C/m2 |
12,70 |
10,96 |
8,96 |
6,91 |
5,00 |
3,30 |
1,95 |
1,00 |
0,44 |
|
S eff K 11 / £ 0 |
730 |
663 |
582 |
509 |
439 |
349 |
263 |
191 |
122 |
|
S eff к 33 / £ 0 |
635 |
567 |
492 |
413 |
345 |
270 |
199 |
130 |
75 |
По данным таблицы 1 построены зависимости эффективных упругих модулей и пьезомодулей от процента пористости [15] , которые представлены на рис. 2.
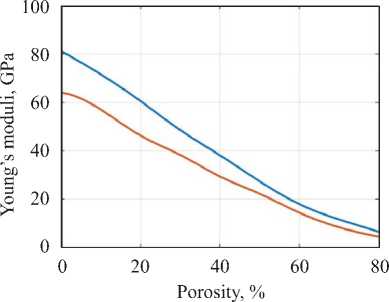
а)
Рис. 2. Зависимости значений от процента пористости [15] : а — упругих моделей; б — пьезомодулей
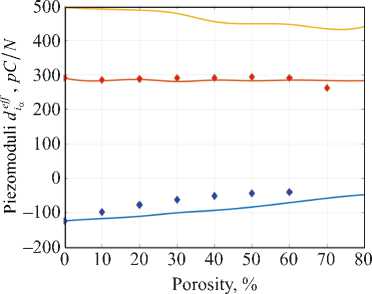
б)
В соответствии с результатами, представленными на рис. 2, модуль упругости E 1 убывает значительно быстрей, чем пьезомодуль d 15 .
Построение прикладной теории
Построенный метод расчета состоит из решения двух задач: в первой рассматривается изгиб под действием механической нагрузки при нулевой разности потенциалов, во второй — моделируется сдвиг, вызванный разностью потенциалов при отсутствии механической нагрузки. В обоих случаях учитывается отсутствие зарядов на лицевых поверхностях пластины. При действии механической нагрузки и разности электрических потенциалов результаты двух задач складываются в силу линейности задачи.
Действие механической нагрузки, потенциалы на электродах равны нулю. Принимаются гипотезы типа Кирхгофа-Лява относительно равенства нулю нормальных напряжений, а для перемещений:
u 3 = UZ 2 ( x ) , u 1 =
—
z .
Распределение электрического потенциала по толщине предполагается квадратичным и симметричным: , . ( z I ( z I Г z 2 I
ф = Ф 1 ( x ) z I 2 , 1 1 h 1 + Ф 1 ( x ) z 1 1 + 2— I h 1 + Ф 2 ( x ) I 1 — 4— I .
к h 7 к h 7 I h 2 )
Для учета граничных условий на концах пластины ( x = 0, l ) получено выражение для поперечной силы:
c 13 e 33
8 c 33 g 33 + 8 e 23 8
—
Q i =
+
—
к
1 ^^^^^^> ^^^^^^^^a
к
—
12 e 15
— c n
c 13
—
( c 33 g 33 + e 323 ) h 2
c 33
(, .„2
1 8 c 33 g 33 + 8 e 33
2 ( c 33 g 33 + e 33 ) h2
—
+ e 3i
— h h2
—
8 c 33 g 33 + 8 e 23 8
—
( c 33 g 33 + e 323 ) h 2 h 2
(^ ( x к
h 3 —
e 33 ( c 13 e 33 h 2 — c 33 e 31 h 2 ) ( c 33 g 33 + e 323 ) h2
c 33
—
c 13
e 31 ( c 13 e 33 h 2 — c 33 e 31 h 2 ) ( c 33 g 33 + e 23 ) h2
h 3
—
1 e i5 ( c 13 e 33 h 2 — c 33 e 31 h 2 ) h
c 33 g 33 + e 33
d T UZ 2 ( x ) I . dx3 v к
С учетом равенства нулю нормальной компоненты вектора электрической индукции на лицевых поверхностях ( z = ± h ), уравнения для неизвестного прогиба UZ 2 ( x ) и распределения электрического потенциала Ф 2 ( x ) имеют вид:
c 13 e 33
—
к
( (
+
^^^B ^^^^^(
—
—
— c 11
кк
—
1 2 e 15
c 13
—
8 c 33 g 33 + 8 e 23 8
( c 33 g 33 + e 33 ) h
c 33
+ e 3i
8 c 33 g 33 + 8 e 23
( c 33 g 33 + e 323 ) h2
—
8 h 2
h 3 —
(. .„2
1 8 c 33 g 33 + 8 e 33
2 ( c 33 g 33 + e 33 ) h2
—
— h h 2
—
V d2 I e15h J—-Ф2 (x)| + кdx2 V 7J
e 33 ( c 13 e 33 h 2 — c 33 e 31 h 2 ) ( c 33 g 33 + e 23 ) h2
c 33
1 e i5 ( c i3 e 33 h 2 — c 33 e 31 h 2 ) h
, 2
c 33 g 33 + e 33
—
к
к
c 13
e 31 ( c 13 e 33 h 2 — c 33 e 31 h 2 ) ( c 33 g 33 + e 323 ) h2
h 3
4 , . I ,
4 uZUZ 2 ( x ) I — W 2 p hUZ 2 (x) — p ( x ) = 0, dx 4 )
Механика
2 8 c зз g зз + 8 e 33 8
■33 ^ ( c 33 g 33 + e 23 ) h 2 h 2 ^
--g 33
c 33
+ - g 11
- 2 g ii
g 33 ( c i3 e 33 h 2 - c 33 e 31 h 2 ( c 33 g 33 + e 323 ) h 2
8 c 33 g 33 + 8 e 23
( c 33 g 33 + e 23 ) h 2
1 8 c 33 g 33 + 8 e 33
2 ( c 33 g 33 + e 33 ) h 2
e 33
4 h 2
h 2
8 h 2
Ф2 (X) +
d 2
yr ф 2 ( x ) dx
• 13 e 33 h 2 - c 33 e 31 h 2 ( c 33 g 33 + e 33 ) h 2
c 33
d y UZ 2 ( X ) dx 2
1 g 11 ( c 13 e 33 h 2 - c 33 e 31 h 2 ) ^ -^-4UZ 2 ( x )
-
24 c 33 g 33 + e 33
Задана разность потенциалов, механическая нагрузка равна нулю. Предполагается независимость поперечного смещения от толщины и равенство нулю продольного перемещения и квадратичное распределение электрического потенциала по толщине (3) :
u 3 = UZ 2 ( x ) , u 1 = 0 . (7)
Выражение для поперечной силы:
Q 1 =- c 44 1 —UZ 2 ( x ) I h - e 15 1 — Ф 2 ( x ) | h.
I dx J I dx J
С учетом равенства нулю нормальной компоненты вектора электрической индукции на лицевых поверхностях ( z = ± h ), уравнения для неизвестного прогиба UZ 2 ( x ) и распределения электрического потенциала Ф 2 ( x )
имеют вид:
-
- c 44 1 -^—-UZ 2 ( x ) | h - e 15 1 -^-Ф 2 ( x ) | h - p ( x ) - W 2p hUZ 2 ( x ) = 0, I dx2 2 I dx2 х 2
d 2 d 2
e 15 —2 UZ 2 ( x ) - g 11 —2 Ф 2 ( x ) = 0.
dx 2 dx 2
Результаты исследования. Проведено сравнение результатов расчетов по предложенным прикладным теориям с расчетами колебаний пьезоэлемента ( l = 0,1 м, h = 0,01 м) на частоте равной 100 с-1 методом конечных элементов в ACELAN [16] .
В первой задаче, определяемой уравнениями (5) и (6), при задании равномерно распределенной нагрузки p ( x ) = 1000 Па·м и с граничными условиями:
d-UZ 2 ( 0 ) = 0, Q i | x = 0 = 0, Ф 2 ( 0 ) = Ф 2 ( l ) = 0, UZ 2 ( l ) = 0, d-UZ 2 ( l ) = 0 (11)
dx dx получены следующие результаты, представленные на рис. 3, 4.
Расчеты показали, что погрешность в определении вертикального смещения — 5,8 %, а для горизонтального смещения составляет 1,2 %.
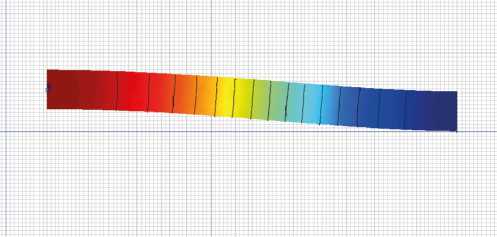
а)
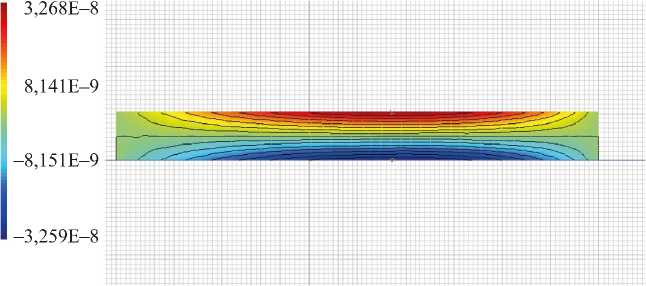
Рис. 3. Вертикальное смещение в ACELAN в первой задаче: а — распределение; б — график на верхней границе
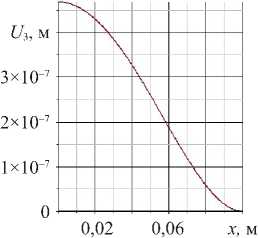
б)
а)
Рис. 4. Горизонтальное смещение в ACELAN в первой задаче: а — распределение; б — график на верхней границе
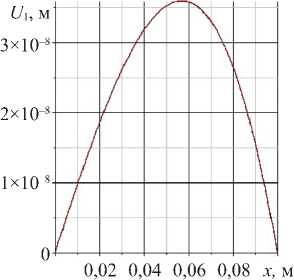
б)
Во второй задаче, определяемой уравнениями (8) и (9), при задании нулевой нагрузки p ( x ) ≡ 0, разности потенциалов V 0 = 100 В и граничными условиями:
= 0, Ф 2 ( 0 ) = 0,Ф 2 ( l ) = V 0 , UZ 2 ( l ) = 0
получены следующие результаты, представленные на рис. 5, 6.
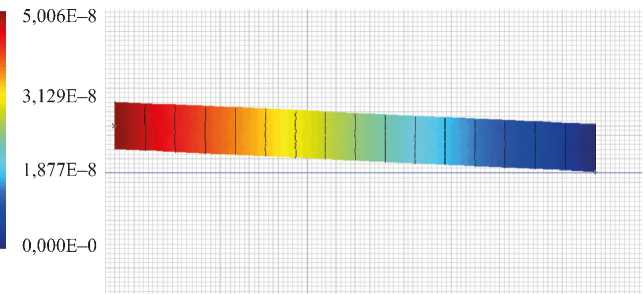
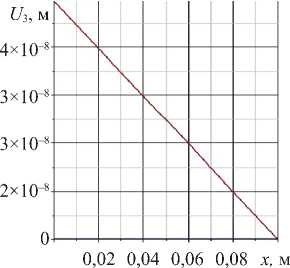
а) б)
Рис. 5. Вертикальное смещение в ACELAN во второй задаче: а — распределение; б — график на верхней границе
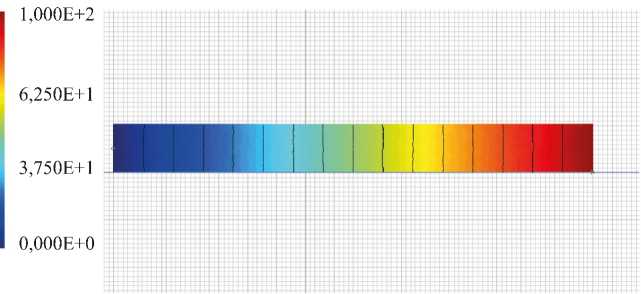
а)
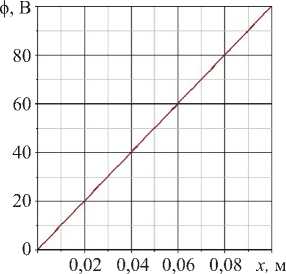
б)
Рис. 6. Электрический потенциал в ACELAN во второй задаче: а — распределение; б — зависимость от продольной координаты в середине толщины
Расчеты показали, что погрешность в определении вертикального смещения составляет 0,8 %, а для электрического потенциала — менее 1 %. Следует отметить, что значения горизонтального смещения, рассчитанные в ACELAN, оказались на три порядка меньше максимального вертикального смещения, что говорит об адекватности гипотезы (7).
При задании механических нагрузок и разности потенциалов погрешность предложенного метода оказалась порядка 6 % для компонент перемещения и электрического потенциала.
Механика
Обсуждение и заключение. Как отмечалось в цитируемой литературе, одновременное использование изгиба и сдвига пьезоэлемента может значительно повысить его эффективность. Кроме этого, использование пористой керамики в силу различных зависимостей упругих модулей и пьезомодулей от процента пористости также улучшает выходные характеристики ПЭГ.
В настоящей работе в силу линейной постановки в теории электроупругости удалось построить прикладную теорию расчета изгибно-сдвиговых колебаний пьезоэлемента в низкочастотной области, которая состоит из решения двух задач: в первой действуют механические нагрузки при нулевых потенциалах, а во второй — наоборот — нулевые механические нагрузки и задана разность потенциалов. На основе различных гипотез о распределении механического и электрического полей получены две краевые задачи для систем обыкновенных дифференциальных уравнений, которые решались аналитически. Проведено сравнение результатов расчета смещений и электрического потенциала по предложенному методу и с помощью МКЭ, реализованного в пакете ACELAN. Эти расчеты подтвердили применимость предложенного метода, погрешность для которого в вычислении вышеуказанных характеристик составила 6 %. Такой точности достаточно для инженерных расчетов, поэтому предложенный метод может быть применен при проектировании пьезоэлектрических устройств, в том числе при сборе и накоплении энергии. Дальнейшее развитие этой прикладной теории будет направлено на охват более широкого частотного диапазона, включая первый изгибно-сдви-говый резонанс.
Список литературы Об одном методе расчета изгибных и сдвиговых колебаний пористого пьезоэлемента в низкочастотной области
- Liang Zhou, Jing Sun, Xuejun Zheng, Shuifeng Deng, Jihe Zhao, Jihe Zhao, et al. A Model for the Energy Harvesting Performance of Shear Mode Piezoelectric Cantilever. Sensors and Actuators A: Physical. 2012;179:185-192. http://doi.org/10.1016/i.sna.2012.02.041
- Dung-An Wang, Nine-Zeng Liu. A Shear Mode Piezoelectric Energy Harvester Based on a Pressurized Water Fow. Sensors and Actuators A: Physical. 2011;167(2):449-458. https://doi.org/10.1016/i.sna.2011.03.003
- Shreya Baneijee, Sitikantha Roy. A Timoshenko like Model for Piezoelectric Energy Harvester with Shear Mode. Composite Structures. 2018;204:677-688. https://doi.org/10.1016/i.compstruct.2018.07.117
- Yanping Kong, Jinxi Liu. Vibration Confinement of Thickness-Shear and Thickness-Twist Modes in a Functionally Graded Piezoelectric Plate. Acta Mechanica Solida Sinica. 2011;24(4):299-307. https://doi.org/10.1016/S0894-9166(11)60031-1
- Xiangyu Gao, Xudong Xin, Jingen Wu, Zhaoqiang Chu, Shuxiang Dong. A Multilayered-Cylindrical Piezoelectric Shear Actuator Operating in Shear (d^) Mode. Applied Physics Letters. 2018;112:152902. http://doi.org/10.1063/L5022726
- Jikun Yang, Qiang Huan, Yang Yu, Jingen Wu, Zhaoqiang Chu, Mohammadjavad Pourhosseiniasl, et al. Tailoring Artificial Mode to Enable Cofired Integration of Shear-type Piezoelectric Devices. Advanced Science. 2020;7(17):2001368. https://doi.org/10.1002/advs.202001368
- Zejun Yu, Shuxiang Dong, Daining Fang. Theoretical Analysis on Shear-Bending Deflection of a Ring-Shape Piezoelectric Plate. AIPAdvances. 2016;6(2):025124. https://doi.org/10.1063/L4943219
- Ewald Benesa, Helmut Nowotny, Stefan Braun, Stefan Radel, Martin Greoschl. Analytical Sensor Response Function of Viscosity Sensors Based on Layered Piezoelectric Thickness Shear Resonators. Physics Procedia. 2015;70:236-240. http://doi.org/10.1016/i.phpro.2015.08.144
- Hui Lia, Shengnan Shenb, Kensuke Amemiya, Bo Liu, Hejun Du. Simulation of Piezoelectric Flying Height Control Slider Using Shear-Mode Deformation. Physics Procedia. 2011;16:101-110. https://doi.org/10.1016/i.phpro.2011.06.115
- Zenkour AM, Alghanmi RA. Stress Analysis of a Functionally Graded Plate Integrated with Piezoelectric Faces via a Four-Unknown Shear Deformation Theory. Results in Physics. 2019;12:268-277. https://doi.org/10.1016/i.rinp.2018.11.045
- Mohammad Malikan. Electro-Mechanical Shear Buckling of Piezoelectric Nanoplate Using Modified Couple Stress Theory Based on Simplified First Order Shear Deformation Theory. Applied Mathematical Modelling. 2017;48:196-207. https://doi.org/10.1016/i.apm.2017.03.065
- Bo Xue, Emmanuel Brousseau, Chris Bowen. Modelling of a Shear-type Piezoelectric Actuator for AFM-based Vibration-assisted Nanomachining. International Journal of Mechanical Sciences. 2023;243:108048. https://doi.org/10.1016/i.iimecsci.2022.108048
- Белоконь А.В., Еремеев В.А., Наседкин А.В., Соловьев А.Н. Блочные схемы метода конечных элементов для динамических задач акустоэлектроупругости. Прикладная математика и механика. 2000;64(3):381-393. URL: https://pmm.ipmnet.ru/ru/Issues/2000/3 (дата обращения: 04.03.2024). Belokon' AV, Eremeev VA, Nasedkin AV, Solov'ev AN. Partitioned Schemes of the Finite-Element Method for Dynamic Problems of Acoustoelectroelasticity. Journal of Applied Mathematics and Mechanics. 2000;64(3):367-377. https://doi.org/10.1016/S0021-8928(00)00059-9
- Kudimova AB, Nadolin DK, Nasedkin AV, Nasedkina AA, Oganesyan PA, Soloviev AN. Finite Element Homogenization of Piezocomposites with Isolated Inclusions Using Improved 3-0 Algorithm for Generating Representative Volumes in ACELAN-COMPOS Package. Materials Physics and Mechanics. 2020;44(3):392-403. https://doi.org/10.18720/MPM.4432020 10
- Nasedkin AV, Oganesyan PA, Soloviev AN. Analysis of Rosen Type Energy Harvesting Devices from Porous Piezoceramics with Great Longitudinal Piezomodulus. Zeitschrift für Angewandte Mathematik und Mechanik. 2021;101(3):e202000129. https://doi.org/10.1002/zamm.202000129
- Наседкин А.В., Скалиух А.С., Соловьев А.Н. Пакет ACELAN и конечно-элементное моделирование гидроакустических пьезопреобразователей. Известия высших учебных заведений. Северо-Кавказский регион. Естественные науки. Спецвыпуск. Математическое моделирование. 200i;Si:i22—125. Nasedkin AV, Skaliukh AS, Soloviev AN. ACELAN Package and Finite Element Modeling of Hydroacoustic Piezoelectric Transducers. Bulletin of Higher Education Institutes. North-Caucasian Region. Natural Sciences. 200i;Si:i22-125. (In Russ.).


