Об одном методе расчета электростатических полей с осевой и трансаксиальной симметрией

Обычно электростатические поля трансаксиальных и осесимметричных корпускулярно-оптических систем описываются в цилиндрической системе координат ρ , ψ , z . Уравнение Лапласа для потенциала φ в цилиндрических координатах имеет вид

1 д   д ф 1 д ² ф д ² ф .

--р—+т—+—г = 0 р др  др р2 ду   дzz

В частном случае, когда потенциал φ зависит только от переменных ρ , ψ , можно ввести безразмерную переменную

П = ln ^р ,                 (2)

ρ ₀

где ρ0 — некоторая характерная длина (обычно радиус цилиндрической поверхности). В переменных п, V потенциал ф (п, V) удовлетворяет двумерному уравнению Лапласа д 2ф + д 2ф = о дп2   дуv

Потенциал ф ( п, у ) является гармонической функцией переменных η , ψ , и для его нахождения может быть использован весь арсенал теории функций комплексной переменной (ТФКП).

В случае трансаксиальных и осесимметричных систем потенциал электростатического поля φ за- висит только от переменных ρ, z и удовлетворяет уравнению

1 д   д ф д 2ф .

--р —+— = 0 0.

р д р д р д z 2

В монографии [1] рассмотрены различные аналитические методы решения уравнения (4) для расчета трансаксиальных и осесимметричных полей. Как известно, Ю.К. Голиков был приверженцем и знатоком аналитических методов. Особенно ему нравился способ Саулита, позволяющий восстановить пространственное распределение потенциала по его распределению в средней плоскости z = 0 трансаксиальной системы или на оси симметрии z осесимметричных систем.

Наиболее общим методом решения граничных задач для уравнения (4) является стандартный метод разделения переменных [2]. При этом потенциал представляется в виде рядов функций Бесселя. Однако эти ряды обычно плохо сходятся и неудобны для проведения численного расчета траекторий частиц (см., например, [3]).

ОСНОВНАЯ ИДЕЯ МЕТОДА

Если в уравнении (4) перейти к безразмерным переменным п , Z = z/р 0 , используя замену (2), то получим следующее уравнение для потенциала ф ( п,^z ) :

е .2 , S ^ +^ = о.

д п2 д Z1

Отметим, что в области р = р₀ переменная П = 0 и потенциал ф ( п, Z ) удовлетворяет двумерному уравнению Лапласа. Будем искать потенциал ф ( п, Ф ) в виде суммы двух слагаемых

ф ( п , ^z ) = ф ^<о> ( п , ^z ) + Ф ^<П ( п , ^z ) .         (6)

Здесь ф⁽⁰⁾ ( п, ф ) — гармонический потенциал, удовлетворяющий двумерному уравнению Лапласа

д 2 ф⁽⁰⁾ д ² ф ⁽⁰⁾ дп^{2 +} д Z ^г

и заданным граничным условиям. С помощью методов ТФКП он может быть найден в замкнутом виде. Тогда второе слагаемое ф ⁽¹⁾ ( п , ф ) удовлетворяет нулевым граничным условиям Дирихле и является решением следующего неоднородного уравнения:

РАСЧЕТ ПОЛЯ ДВУХЭЛЕКТРОДНОЙ ТРАНСАКСИАЛЬНОЙ ЛИНЗЫ

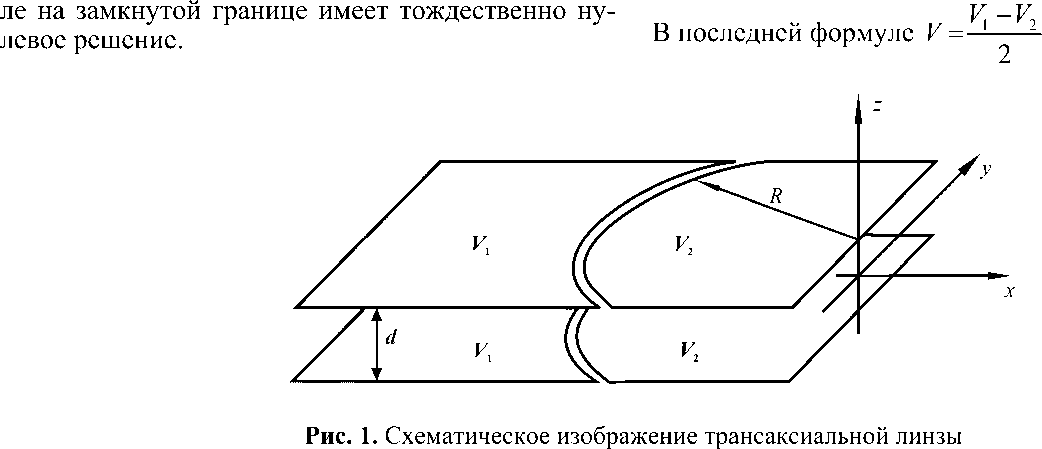
Простейшая иммерсионная трансаксиальная линза схематически изображена на рис. 1, где показана также декартова система координат x , y , z . Трансаксиальная линза представляет собой две параллельные пластины, разрезанные прямым круговым цилиндром радиуса R , ось которого совпадает с осью z [4].

Начало декартовой системы координат находится в средней плоскости линзы z = 0, V 1 и V ₂ — потенциалы электродов, d — расстояние между пластинами. Зазор между электродами считается бесконечно узким. Вдали от краев пластин электростатический потенци ал φ зависит только от переменных р = x ² + у¹ и z . Вводя безразмерные переменные η и ζ :

,-2 „ д ф + д 2 ф ⁽¹⁾ д п ² д Z^г

= ( 1

- е ^{- 2 п} )

д v °

д п ²

^п = ln ^р

_Z =—

R ,

В большинстве случаев уже слагаемое ф^⁰ (п, ф ) является достаточно хорошим приближением для расчета потенциала. Это связано с тем, что большие значения производная д ² ф⁽⁰⁾     д²ф⁽⁰⁾                                   _

---— =--— в правой части (8) принимает в дп2      дZ2

области, где п = 0. В этой области ф(1) (п, ф) приближенно удовлетворяет двумерному уравнению Лапласа получим уравнение для потенциала (5). Решение этого уравнения, удовлетворяющее граничным условиям в рассматриваемой трансаксиальной линзе, представим в виде:

ф ( п , Z ) = V ^+ F ( п , Z ),         (11)

где функция F ( η , ζ ) удовлетворяет следующим d граничным условиям в полосе Z =± Z₀ =±-- :

д ² ф⁽¹⁾   д²ф⁽¹⁾   „

—^Г +   7 = 0, дп2 д Z2

V для п >  0, F ( п , ± Z 0 ) =^ _v

^ - V для п <  0.

которое при нулевых граничных условиях Дирих-

.

Решение уравнения (5) для функции F ( η , ζ ) представим в виде

F ( n , Z ) = F ⁽⁰⁾( n , Z ) + F ^тП , Z ).       (13)

d ² р ⁽⁰⁾      у ² р ⁽⁰⁾

a u ² = a v v

Здесь F ⁽⁰⁾ ( η ζ ) гармоническая функция удовлетворяющая граничным условиям (12):

2 V (      1 — u 1 + u I

F ^(o) ( n , Z ) =- V +—I arctg---- + arctg---- I ,   (14)

П V v         v J

4 V 1 — u            1 + u

---v <-------------- 7 +-------------- 2

ⁿ     |^ v ² + ( 1 — u ) 2 J    |^ v ² + ( 1 + u ) 2 J

где

d ² F ⁽⁰⁾ d u d v

а слагаемое

u — exp

v — exp

—

nn

V 2 Z o

πζ sin ,

2 ζ 0

—

nn

V 2 Z o

πζ cos ,

2 ζ 0 ^,

2 V I v ² —( 1 — u ) 2       v ² — ( 1 + u ) 2

П |[ v 2 + ( 1 — u )= ] ² ’[ v = + ( 1 + „ ) 2 ] ²

F ^{( 1 )} ( n, Z ) удовлетворяет

следую-

щему уравнению

е

2    (1)       2    (1)

^{2 n} ^- F -i^^-= (1 — е -^{2 n} ) a n ² a z ²

d ² f ^(o)

d n²

и нулевым граничным условиям в полосе Z —± Z _o •

Уравнение (16) будем решать численно, перейдя от уравнения в частных производных к системе обыкновенных дифференциальных уравнений для функций F'^ ( Z ) = F ⁽¹⁾ ( n k , Z ):

_d2 _Fk (1) d ζ ²

= (1 — е ^{— n}

)

( d ² F ⁽⁰⁾ | V ^d n ² J _k

е ^{— 2 n} ‘

I

V ^d n ² J k

. (17)

Здесь k — — n , — n + 1,..., n — 1, n , переменная n при

нимает дискретные значения n _k — kh индекс " k "

у частных производных означает, что эти производные берутся при значении n — n _k , причем

2    (1)             (1)           (1)        (1)

^d F _ F k + 2   ² F k  ⁺ F k — 2

. dn² к 4 h²

k

где h — шаг дискретности по η . Приведем также выражение для частной производной:

5 ² f ⁽⁰⁾    d ² f ⁽⁰⁾

d n ²      S u²

■ u I +

V^d n J

„ d ² F ⁽⁰⁾ d u d v  d ² F ⁽⁰⁾

+ 2---+--— du d v dn Sn Sv

V

2 d v | d n J

.

Используя формулы (15), (16), найдем производные, входящие в (19):

d u d n d v d n

exp 2 ζ 0

—

nn

V 2 Z o

πζ sin ,

2 ζ 0

π

--exp

2 ζ 0

—

nn

V 2 Z o

πζ cos .

2 ζ 0

Систему уравнений (17) можно проинтегрировать численно, задавая нулевые начальные условия на прямой Z _— Z _o :

( F¹^ I

FZ 1 _ o, -F ^ L -,_ o. (23) k         o                           Z Z

V ^{- Z} J ^o

Отметим, что F _o ⁽¹⁾ ( Z ) = o.

РАСЧЕТ ПОЛЯ ЦИЛИНДРИЧЕСКОЙ ЗЕРКАЛЬНОЙ СИСТЕМЫ

С ЗАКРЫТЫМИ ТОРЦАМИ

В качестве примера расчета поля осесимметричной системы рассмотрим цилиндрический зеркальный анализатор с закрытыми торцами (ЦЗАЗТ), предложенный в работе [3]. Схематически система электродов такого анализатора представлена на рис. 2. Здесь R ₁ , R ₂ — радиусы внутренней и внешней цилиндрических поверхностей соответственно, l — расстояние между торцевыми электродами. Будем считать, что потенциал торцов и внутреннего цилиндра равен V _o — 1, а потенциал внешнего цилиндра равен V .

Введем безразмерные переменные η и ζ согласно (10), где r — VR7r2 .             (24)

В переменных n и Z потенциал ф ( Z , n ) удовлетворяет граничным условиям в симметричном

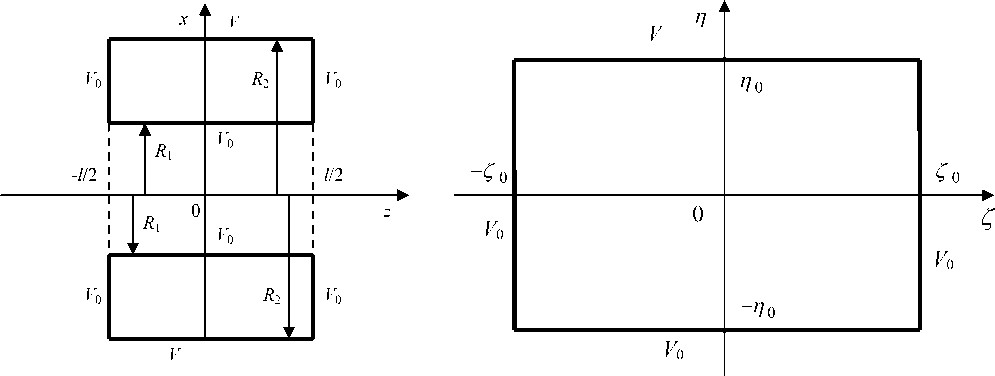
Рис. 2. Изображение проекции электродов ЦЗАЗТ на плоскость xz сопутствующей декартовой системы координат

Рис. 3. Граничная задача в ζη -плоскости

прямоугольнике, представленном на рис. 3. Потенциал верхнего электрод п = П ₀ равен V , а остальные электроды имеют потенциал V 0 = 1. Величины η ₀ и ζ ₀ на рисунке определяются выражениями:

П о = In

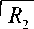
R 1

Интегралы J ₁ , J ₂ в выражениях (27), (28) являются эллиптическими. Их значения находились численно, причем в δ -окрестности особых точек ± 1, ± а интегралы вычислялись аналитически, что позволило получить точность расчета не хуже, чем δ ² :

z =—

0   2 R

Отобразим этот прямоугольник на верхнюю полуплоскость комплексной плоскости w = u + i v , используя конформное преобразование [5]:

J- = 7 I d u 2 +             ,(29)

\ (1 - u )(1--r) A 21 1

V             a V V a )

a - 5

w z + in = iПо + CJ j ^     2 .    (26)

0 w

. (1 ^- w ⁾⁽1-- _r)

а ²

^J 2 = J

d u

I ( u ² - 1)(1 - u^ )

a ²

+

Здесь точки w -плоскости ± 1 соответствуют вершинам ± Z 0 + i n 0 , а точки ± а — вершинам ± Z ₀ - i п 0 . Для определения постоянных нужно вычислить следующие интегралы:

δδ

+ —.          Г + —,

J 2 1 1 - 4т I   j a ( a ² - 1 ) 1 1 + ¹ I

\ V a ) Xj ^v 'V a)

CJ , = C J

d u

(1 - и ²)(1 - u 2 )

a ²

= Z 0

В таблице для различных значений параметра а приведены вычисленные значения интегралов J ₁ , J ₂ , а также их отношение, равное

J l = z 0 .

J ₂ 2 η ₀

а

- i CJ 2 = - i C l" . d u    = =- i2 n 0 . (28)

\ ( u ² -1)(1 --)

a ²

Распределение гармонического потенциала в w -плоскости определяется выражением:

1 V - 1 \       1 - u 1 + и

F ( ) ( u , v ) = 1 +-----1 arctg----- + arctg-----

П V v          v

Значения интегралов J ₁ , J ₂ в зависимости от величины параметра а

а	J 1	J 2	J 1 / J 2
1.1	2.318616	1.639984	1.413805
1.2	2.064762	1.712320	1.205827
1.5	1.807818	1.900835	0.951065
2.0	1.684159	2.153757	0.781963
3.0	1.615925	2.5262828	0.639645

Для нахождения гармонической части потенциала ϕ ⁽⁰⁾ ( ζ , η ) , определяющей поле ЦЗАЗТ, необходимо в выражении (32) перейти от переменных u , v к переменным ζ , η с помощью конформного преобразования (26). Поправка ϕ ⁽¹⁾ ( ζ , η ) удовлетворяет нулевым граничным условиям в прямоугольнике, представленном на рис. 3, и может быть найдена путем решения системы обыкновенных дифференциальных уравнений (17).

ЗАКЛЮЧЕНИЕ

В работе предложен метод расчета поля, позволяющий находить простые замкнутые аналитические выражения для пространственного распределения потенциала в трансаксиальных и осесимметричных линзах и зеркалах. В качестве примера получены аналитические выражения для потенциала двухэлектродной трансаксиальной линзы и осесимметричной зеркальной системы. Хотя полученные выражения для потенциала являются приближенными, они с хорошей точностью отражают основные особенности поля рассмотренных систем.