Об одном методе решения краевой задачи термоупругости для растущего многослойного шара

Формулировка краевых задач термоупругости для непрерывно растущих многослойных тел возникла из потребностей строительной механики и была рассмотрена в ряде фундаментальных работ, результаты которых получили обобщение в [1, 2]. Впоследствии подобный подход был применен при моделировании процессов кристаллизации, нанесения покрытий, намотки с отверждением и т.д. [29]. Установлено, что в растущем теле скорости компонент термоупругого поля удовлетворяют системе уравнений, которая математически эквивалентна аналогичной системе краевой задачи термоупругости для тела со стационарными границами. Отличие заключается в краевых условиях на поверхности роста, где начальные напряжения в присоединяемом элементарном тонком слое и геометрия тела задают граничное условие для скоростей напряжений. При заданных граничных условиях для определения скоростей можно использовать известные решения классической тер

Плотников Андрей Николаевич, кандидат технических наук, доцент кафедры производства летательных аппаратов и управления качеством в машиностроении. Докукина Ирина Александровна, кандидат технических наук, доцент кафедры производства летательных аппаратов и управления качеством в машиностроении. Савич Екатерина Константиновна, аспирант моупругости, а результирующие значения в растущем теле определяются путем интегрирования соответствующих скоростей с учетом начальных значений в растущем слое [1-9]. Но при этом слоистая неоднородность растущего тела ограничивает применимость решений, полученных в классической теории [10]. В связи с этим известные в литературе аналитические решения пространственных задач для растущих и многослойных тел по существу исчерпываются телами простой формы и получены либо для неоднородности, вызванной, главным образом, реологией материала растущего слоя [1-9], либо для многослойного тела со стационарными границами при допущениях, скорее адекватных также для случая развитой пластической деформации [10]. Однако в многослойном теле адгезионная прочность разнородных слоев зачастую может быть существенно меньше напряжений, необходимых для развития реологических процессов. Кроме того, напряжения в теле возникают и эволюционируют по мере роста самого тела. В связи с этим рассматриваемая задача термоупругости для растущего многослойного шара, как представляется, сохраняет свою актуальность.

1. ПОСТАНОВКА ЗАДАЧИ В СКОРОСТЯХ И ВЫВОД КРАЕВЫХ УСЛОВИЙ НА ПОВЕРХНОСТИ РОСТА

При постановке задачи приняты следующие допущения:

непрерывное послойное наращивание, заключающееся в перемещении всех точек поверхности роста по нормали с равными скоростями;

квазистатическое равновесие растущего тела, заключающееся в малости скоростей роста, изменения температуры и внешних нагрузок по сравнению со скоростью распространения упругих возмущений (скоростью звука в твердом теле);

отсутствие реологических процессов, заключающееся в сохранении упругости основного и растущего слоев.

При сделанных допущениях относительно процесса роста напряжения, деформации и температура зависят от времени не явно, а опосредованно, через толщину растущего слоя h (в предположении монотонного возрастания h ( t ) ). Поэтому вместо скоростей можно использовать частные производные по параметру h , имеющие смысл относительных скоростей компонент термоупругого поля, и напряжения, деформации и температура примут вид интегрального представления:

h a _J

daj(r,5d. e J^r,5 85    ^ i J d^

Т= J d! <^) d ^

^{J 9} 5    ⁴

(1.1)

в исходном теле

,z x h da j ( r , . )

^, _ a ^r) + J _ d5, h *( r)

,z x h Se ij i r , 5 ) ^e a ^_ j ^{r )+} J —^. d ⁵

h •( r) 95’

т = т*(r)+ J J^r5d5

h r ) ⁹ 5

(1.2)

в растущем слое, где h — h* (r ) - совокупная толщина вышележащих слоев для точки r , а a ij , eij , T - значения соответствующих величин на поверхности роста.

При выводе граничного условия на поверхности роста положим внешние нагрузки на ней равными нулю и рассмотрим сферическую поверхность роста положительной и отрицательной кривизны. Используя подход, заключающийся в расчленении упругого тела и приложении к образующимся частям эквивалентных нагрузок, приходим к следующей схеме рассуждений.

Пусть при формировании и закреплении на основе тонкого сферического слоя толщиной Дh компоненты термоупругого поля в растущем теле (за вычетом слоя Дh ) приобретают приращения ДT _ T(r, h + Дh) — T(r, h) ; Даг(9) = ar(9) (r,h + Дh)— ar(9)(r, h) удовлетво- ряющие условиям термоупругого равновесия. Для однозначного определения Даг(9) кроме ДT необходимо знать величину радиальной компоненты Даr , возникающую на поверхности r _ r * (h) в результате воздействия слоя Dh. При этом, так как на поверхности роста отсутствуют внешние нормальные нагрузки, то Дсг (r*(h),h) _ ar (r* (h),h + Дh). Причиной возникновения нормального давления на поверхности r _ r* (h) является наличие в слое Дh окружных (кристаллизационных) напряжений а9 (h) _ ak (h). Для установления связи между Дar (h) и а*е (h) возьмем произвольно ориентированное диаметральное сечение составного шара и рассмотрим равновесие элементарного слоя Дh в проекциях на ось, перпендикулярную плоскости сечения (рис. 1).

В случае вогнутой поверхности роста (положительной кривизны, рис.1) будем иметь:

^п " 2

2п(R—h)ak (h)SJ — 2n(R — h)2Да* Jsin9cos9d9 _ 0, откуда, устремив Дh^0, получим , da+ _ 2ak(h) dh    R — h

(1.3)

где R-h – текущий радиус кривизны поверхности роста, знак “–” в первом равенстве следует из того, что направление силы, действующей на приращиваемый слой со стороны оправки при a k >  0 , противоположно внешней нормали к поверхности основы. Таким образом, при наращивании на внутреннюю сферическую поверхность слоя с растягивающими кристаллизационными напряжениями на границе основного и растущего слоев возникает радиальное растяжение.

Аналогичным образом для случая выпуклой сферической поверхности (отрицательной кривизны, рис. 2), получим

5 a — _ ^{2 a} k ⁽ h ) ^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^в                 ^^^^^^^s ^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^1

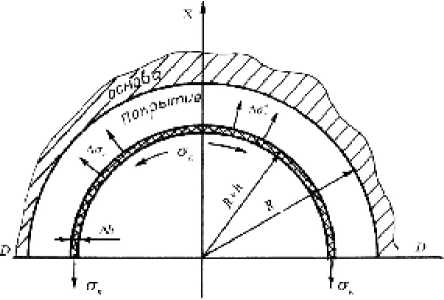
Рис. 1. Равновесие упругого слоя на внутренней сферической поверхности

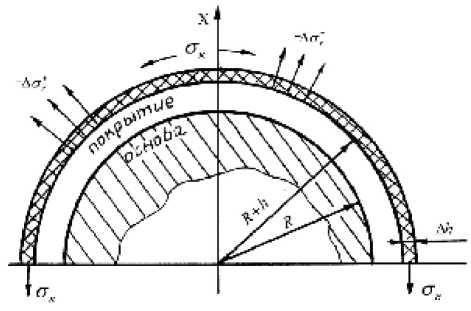
Рис. 2. Равновесие упругого слоя на внешней сферической поверхности

где h – толщина растущего слоя; b+h – радиус шара, а штрихом обозначены частные производные по h.

Напряжения, действующие в исходной части растущего шара (0 < r < b ), найдем, интегрируя соответствующие скорости в пределах [0; h ]

a'h I i b + ^f               i                 1

" ⁼i^ j | _ j ^{T Pf ) p d p -}7 j ^{T( p} , ^ ^{) p d p}^ d ^- (2.3)

^M 0 \ ( ^{b + f} ) 0                 * 0              J

Используя формулы дифференцирования интеграла, зависящего от параметра, интегрирования “по частям” и полагая начальную температуру нулевой, получим

Знак “–” в (1.4) указывает на то, что в этом случае растянутый внешний слой оказывает давление на оправку.

Условие равновесия растущего слоя на поверхности цилиндра имеет похожий вид:

" r

h j 0

1 a E |    1

1 - m \ ( b + h ) ³

b+h                        r j T(p, h)p2 dp —3 j T(p, h)p2 dp -

0                    r 0

3 ^b 1

^T ( ^b + f ^, f ) - -- j ^T( pf )p² d p ^{( b + f )} 0

d f

b ^{+ f}

> .

(2.4)

"l^ " k ( h )

5 h     R m h '

(1.5)

Кроме того, в цилиндре возникает осевое сжатие величиной

5 P; d h

- 2 n ( R m h "  ( h ) .

(1.6)

Таким образом, кристаллизационные напряжения в растущем слое задают граничные скорости радиальных напряжений и начальные значения окружных напряжений. Однако и при отсутствии кристаллизационных напряжений возникают напряжения из-за необратимого формоизменения тела, заключающемся уже в самом процессе роста.

2. ТЕМПЕРАТУРНЫЕ НАПРЯЖЕНИЯ В РАСТУЩЕМ ОДНОРОДНОМ ШАРЕ

В качестве иллюстрации рассмотрим однородный шар радиусом b, на поверхности которого растет слой толщиной h из того же материала. Температурное поле T(r,h) будем считать заданным, кристаллизационные напряжения и соответственно граничную скорость (1.4) положим нулевыми.

Используя известное решение для температурных напряжений в шаре [11, 12], можем определить поле скоростей напряжений в растущем шаре:

"

2 a E I     1     b ⁺ + h                    1 Г                 1

1--- 7, ,v l ^{T (} P ^,h ) P d p -     ^T( P ^,h ) p d p\ ,(2.1)

^{1 -} m \ ( b + h ) 0               ^r 0            P ⁷

, _ cE [ 2

6 = V-M\pl

b+h                      r jT (p, h)p dp+- jT (p, h)p dp-T (r, <(2.2)

0               r 0                     J

Аналогично находим окружную компоненту

b + h                        r

" = a E 1R ( P , h)p" d p +-R ( P , h) P 2 d p -

^{1 -} д \ ( b + h ) 0               r 0

-

h

T ( r , h ) - 2 j T ( b + § , § )

0 _

( b + f ) ³

b + T( p , f ) P d p i 7 7 1^(2.5)

0            J ^{b +} fJ

После остывания, которое интерпретируется как наложение температурного поля -Т(r,h), в исходном шаре остается однородное сжатие

2PE hL^ .     - b i f z   ^I df

” - =” • 1 ^ 1 Tb" ^ ^^-( b + f j ^{I( p ,} ? ^{) P} d^ : ■ (2-6)

Рассмотрим выражение в фигурных скобках. Первое слагаемое, очевидно, представляет собой температуру поверхности роста Т*( f ). Второе слагаемое есть ср ед неинтегральная температура растущего шара T ( f ) .

Таким образом, остаточное сжатие в исходном шаре будет равно

h

_ocm _ocm       ^^a-L     *

^r = °9 =^{-       6 (f}’TT^ , (2.7)

1 - M 0 b + f ’ где 6* (f) = T (f) - T (f) — текущая избыточная температура поверхности роста. Для растущего слоя b < r < b + h, подставляя пределы интегрирования [r-b;h] и проделав аналогичные вычисления, получим

"r = ^a l ( b + ¹ h ) ^{7 j T 1 P , h} ) ^P" ^{d P} - r ¹^ ^{j T 1 P ,}r - ^{b 1 P 2 d P} -

• ^-    "13 j ^{T (} P ^{, h} ) P ² d p ⁺ "13 j ^{T (} P ^{, r - b} ) P ² d p ^{- r} 0                  ^r 0

• -    h T ( b + f , f ) -         + T ( p , f ) p ² d p -<- ¹ .

r - b _               ( b + f ) 0               J ^{b + f} J

(2.8)

Второе и четвертое слагаемое (2.8) в сумме дают ноль, первое и третье равны напряжениям, возникающим при остывании со знаком “-”. Следовательно, остаточное радиальное сжатие в растущем слое будет равно ocm

° r

^{2 a E} f 0* ( 5 ) -d⁵

1 - M r^J b        b + 5 ■

(2.9)

где введено обозначение ф = a T , а величины E, M , а являются функциями радиальной координаты r .

В [13] показано, что подстановкой

x ( r ) = Ц ^ Т ) ⁽ ° 0 ( r ) — ° r ( r ) ) задача ^{(3.1) E ( r} )

сводится к интегральному уравнению типа Воль-терра II рода

Величина G ™c" в растущем слое в тех же обозначениях будет иметь вид

ocm

° 0

а Е

1 — м

h

0 ( r — b ) — 2 J 0 * ( 5 ) r — b

d < b + 5

(2.10)

Таким образом, в растущем слое имеет место неоднородное напряженное состояние, а окружная компонента может претерпевать скачек величиной 0 (0) в точке r = b . Данный пример объясняет механизм возникновения температурной составляющей напряжений в растущем теле. Кроме того, интересным результатом представляется то, что для анализа напряжений не обязательно иметь полное описание температурного поля, определение которого при наличии подвижной границы представляет собой самостоятельную и довольно сложную проблему. Достаточно знать лишь избыточную температуру поверхности роста, которая в ряде случаев может быть определена исходя из физики массо- энергообмена на поверхности роста.

x ⁽ r ) = ^— J K ( r , p ) x ⁽ p ) d p + Р а ¹ f ^ r ) ^— ф ⁽ r ) + C a (3.2) a                         ^{e (} r )                ^{v 7}

с ядром

K ( r , p ) = l^ p) p Li— m ( p )

+2 ^{E (} p ^—2 m ^{( r )}) 1 ₍₃₃₎

E ( r )(1 — m ( p ) ) J . ^(3.3)

Константа C будет определяться из граничных условий

f E’r' *) dr = Р Р a1—m(r) r 2

.

(3.4)

Система уравнений (3.2), (3.4) допускает тождественное преобразование, основанное на оче-

видном соотношении

rbb

J = J — J . Данное пре- aar

образование необходимо при вычислении напряжений в случае выпуклой поверхности роста.

После необходимых преобразований получим интегральное уравнение следующего вида:

3. РЕШЕНИЕ ЗАДАЧИ В СКОРОСТЯХ ДЛЯ МНОГОСЛОЙНОГО ШАРА

b

^{x ( r} ) = J K ^{( r} , p ) ^x( p ) d p ^{+ P} b

r

1 — 2 m ( r )    , .

-_{E (} r ₎- ^{— ф (} r ) + C b , (3.5)

Для определения скоростей напряжений в растущем неоднородном шаре следует решить соответствующую задачу со стационарными границами.

Рассмотрим полый шар a <  r <  b , имеющий сферически симметричное распределение упругих параметров и температуры и давление на границах: o r ( a ) = — P_a , o _r ( b ) = — P_b . Напряженное состояние такого шара будет определяться двумя компонентами напряжений s_r, s_q, двумя компонентами деформаций e_r, e_q, радиальными перемещениями u , также подчиняющимися сферической симметрии и системе уравнений [10]:

^bb 1 + M d p где C b = C a —       —.

a1—м p

(3.6)

Полученные интегральные уравнения (3.2), (3.5) удовлетворяют необходимым и достаточным условиям существования и единственности решения, определяемого в виде интегрального представления с резольвентными ядрами [14]:

r xa (r) = fa (r) — J Ra (r, p)fa (p)dp , (3.7)

a do   2/

—= -(°9

dr r

—

° ,

),

b xb (r) = fb (r) + J Rb (r, p)fb (p)dp , (3.8)

r

E

(1 + m)(1 — 2м)

E

r

°⁰ = ( 1 + м )( 1 — 2 m )

^[ ^_e ⁺ Ms ,

+ 2 ms 0 — ( 1 + м ) ф ] ,

(3.1)

^{— ( 1 +} M ) ф ^],

du

^S r = 3^-’ dr

u

^£ e = ^—, r

^{где f}a ( b ) ⁽ r ) = C a ( b ) ^{+ P}a ( b )  -- ^{ф (} r ) .

Для однородного шара ядро (3.3) и резоль- вента (3.7), (3.8) принимают вид K(r, p) ^ — ,

2                       p

R b ^{( r} , p ^{) =} R a ^{( r} , p ^{) = 3} T . r

В результате получаем известное решение для температурных напряжений в однородном шаре [11,12]. При ограничении

E ( Г )

—7--------- = const , принятом в [10] в зада-3 ( 1 - 2 ц ( r ) )

че, аналогичной (3.1), уравнение (3.2) путем однократного дифференцирования по r приводится к линейному дифференциальному уравнению первого порядка и в результате получаем решение, эквивалентное [10].

Таким образом, интегральное уравнение (3.2) является, по всей видимости, наиболее общей математической формулировкой задачи по определению термоупругих напряжений в неоднородном шаре со сферически симметричной неоднородностью, пригодной как в случае непрерывных Е(г), Ц (r), j(r ), так при наличии у них конечного числа разрывов первого рода [14]. Последний случай является моделью неразрывного многослойного тела.

Далее на основании эквивалентности задачи для растущего шара в скоростях напряжений статической задачи в напряжениях и полученного решения для напряжений в многослойном шаре можем определить скорости напряжений в растущем шаре. Учитывая тот факт, что для растущего шара пределы интегрирования зависят от толщины растущего слоя, получим

^ e ^{( r} . ^{h ) =} ^ r ^{( r} . ^{h ) +} 1 E ^ r ) x + ^{( r} . ^h ) , (3.10)

Л ,)   р-м b + h E ( p ) X- ( p , h ) ,

^ r ⁽ r . h ) = - ^{p (} h ) ^{- 2} J 1 - ЦР   — d p , (3.11)

^ e-(r. h)=t(r. h)+ 1 E^r)x-(r. h), (3.12) где введено обозначение а символы “+”, “-” соответствуют знаку кривизны поверхности роста. Функции x9 (r. h) определяются в результате решения соответствующих интегральных уравнений (3.2), (3.5) с правой частью

Неизвестные функции C± (h) определим из граничного условия, которое при отсутствии нормальных напряжений на стационарной по- верхности будет иметь следующий вид:

|^(rL x+fr.h) dr=-1 p *( h), 1 - ц( r)

a - h/ b +*h E (r) x_ (r. h)         1

Сами компоненты напряжений, соответствующие скоростям (3.9)-(3.12) определяются в результате интегрирования по h с учетом следующих начальных условий:

для исходного тела a <  r <  b

h       '                                  h '

^T = J ^T r ^{( r} . ^ ) d ^ , ^T 9 ± = J ^T ± ^{( r} . ^ ) d ^ ; (3.16) 0                                0

для слоя, растущего на вогнутой поверхности

a - h < r < ah '

a - r

h

T8 = T 9 (a - r)+ JT9 (r.^)d§ ;      (3.17)

a-r для слоя, растущего на выпуклой поверхности b < r < b 9 h

h '

^T r = J ^T r ⁽ r . ^ ) ^d ^ , r - b

h '

^T9 = ^{T ( r - b ) +} J ^T- ^{( r} . ^ ) ^d § .      (3.18)

r - b

Соотношения (3.16)-(3.18) образуют общее решение в напряжениях для многослойного полого шара в процессе квазистатического роста. При последующем выравнивании температуры финальные (остаточные) напряжения будут результатом суперпозиции напряжений (3.16)(3.18) и температурных, возникающих при остывании неоднородного шара. Для определения последних не требуется дополнительных вычислений, а достаточно подставить в найденное ранее поле скоростей (3.9)-(3.12) соответствующие напряжения и действующую избыточную температуру, взятую с обратным знаком.

4. ИССЛЕДОВАНИЕ МОДЕЛИ

Для исследования модели рассмотрим двухслойное сферическое тело с параметрами основного слоя E0, m0, a0и растущего Е1, m1, a1. В этом случае ядро (3.2), (3.5) и резольвента (3.7), (3.8) будут иметь вид

K ^{( r} ’ p )

1 |3, ( r , p ) e D_x

= —1

P I G 1,0 , ^{( Г} ’ P ) ^{e D} 2 ’

новы 0< у Е ( в - 1) <+Г. Значения v < — 0 со ответствует твердому слою на “мягкой” оправ ке. Представляется интересным эффект инвер

-

-

-

R ^{( r} ’ P )

p2 3, (r, p) e Di = r 3 [G1,0’ (r’ p) e D2

где введено обозначение

¹ + A i + 2 Ex ^{(1 - 2} A o )

^{1 - A} 1      E o ^{(1 - A} 1 )

D ₂ - часть обла

сти { p <  r } , в которой E ( p ) * E ( r ) , a D 1 служит ее дополнением.

Поскольку кристаллизационный и температурный механизмы формирования напряжений имеют различную природу и действуют независимо (хотя величина кристаллизационных напряжений может зависеть от температуры), соответствующие компоненты напряжений целесообразно рассмотреть по отдельности.

При анализе кристаллизационной составляющей положим начальные напряжения в растущем слое постоянными ( г ' ( h ) = ст ₀ ) .

Для вогнутой поверхности роста после необходимых преобразований получим

сии знака окружных напряжений в растущем слое. Это возможно при условии exp[ 3 v /(1 - 2 v )] >  1 + v и при толщинах

^ >  ^ 1 = ^{1- 3}V [(1 + v )exp( - 3 v (1 - 2 v )) - 1]/ v .⁽4.⁴⁾

То есть по достижении критической толщины твердого покрытия ( v < - 0,54 ) напряжения в нем на границе с основой из растягивающих переходят в сжимающие.

Для выпуклой поверхности роста подставляя

вместо (4.3)

„ a'      r       h в Z,3 ’ n A ’ ^ A ’ b3     b      b

получим

" r

= -s

г +

= 2 1 .

³ vn

/ 1М vn + 1

^{( п + 1)ln} л _Аз г v (1 - - А + 1

/   п в-П ³,     v + 1

(v+ 1)        ln             , в-1   v(1-2)3 +1

. 2vr 3 - 1,    vn + 1

- +      vn   И1-33 +1’ г =1

- (1 + v ) ( в + 2^ _ln   v + 1

. 3(в-1) vn     v(1-5)3 +1’ где введено обозначение

1 - § <  n <  1

1 <  n <  3/ в

(4.1)

1 - ^ < n < 1

1 < n < #

(4.2)

" s

" S

°' (S)          ’

°0

в = b³ > 1 a

r _ = h     = E o (1 - 2 A 1 )

a ’ a ’ '     £ 1 (1 - 2^)’

_в = 1 + (1 + А о ) в    _v = У ( в - 1)(1 + A ) - 2 в (1 - 2 a )

¹      2(1 - 2 a o ) ’        2(1 - 2 A )( ^ E ( в - 1) + в )

Как видно из (4.1), (4.2), распределение кристаллизационных напряжений в растущем слое образует однопараметрическое семейство с параметром v , величина которого монотонно воз-

1 + a i растает в пределах - 1 <  v <---- —— с рос-

2(1 - 2 A 1 )

том приведенной относительной жесткости ос-

_v =   2(1 - 2 _д ) У е (1 - в ) - в )

V E (1 - в )1 + A ) + 2 в (1 - 2 a ) ^{(   )}

1 + v в xi 1 + v ------(1--_?) In--------------’ 1"^A   7³   (1 + £)³+1/

^{(1 + v )ln} n

3 .

n + v

(1 + ^ ) ³ + v ’

2 1 + v в м 1 + v --(1 +-- r) In--------;-----, 31 - в    2 n³    (1 + ^ ) ³ + v

= 1

1 + ²(1 - v )ln ^ 3      2 n³

3 .

n + v

(1 + ^ ) ³ + v ’

3/ в <  n <  1

1 <  n <  1 + ^

(4.6)

л в <  n <  1

1 <  n <  1 + ^

(4.7)

Диапазон варьирования параметра n в этом случае составит - 1 <  v <  2(1 - 2 A 1 )/(1 + A 1 ), а критическая толщина слоя равна

^ 1 = V(1 + v )exp[3/(2 - v )] - v - 1 . (4.8)

Интересно отметить, что величина скачка окружных напряжений А сте на границе раздела слоев при значениях v <0 (твердое покрытие на мягкой оправке) с ростом толщины так же может менять знак, переходя через ноль. На вогнутой поверхности роста такая ситуация реали- зуется при -1< v <--1 и толщине слоя

e

^ ₊ * = 1 - V[ e (1 + v ) - 1] v .

На выпуклой по-

верхности аналогичные условия имеют вид –

1< v <0 и ^ -

3/ e ^v (1 + v ) - v - 1 .

На рис. 3 представлены эпюры окружной компоненты и интенсивности кристаллизационной составляющей напряжений r i = | г_е - r _r| в растущем слое в зависимости от v . Координата x = 0 соответствует границе с основой, x = 1

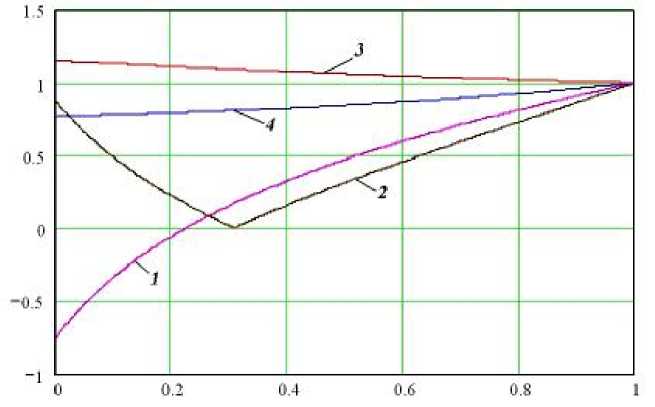
Рис. 3. Распределение окружной компоненты (1,3) и интенсивности кристализационных напряжений (2,4) в растущем слое на вогнутой поверхности: 1,2 – при x = 0.2 и n = -0.9; 3,4 – при x = 0.2 и n = 1.5

– свободной поверхности растущего слоя.

Для выявления отличий в картине напряжений, формирующихся при нагреве и остывании в процессе наращивания рассмотрим монотонное изменение температуры с ростом толщины покрытия, полагая в качестве модельного примера следующие два случая: а) нагрев при наращивании от нулевой температуры ( ф ₀ = 0 ) до температуры ф = ф} и охлаждение до исходной температуры при постоянной толщине покрытия; б) начальный подогрев до температуры ф} , охлаж-

-+ V. ^ф I °e 3.3 I

( в — 1) f

^щ— x ) ³ + 1    v(1 — f + 1

( в + 2 , ) f ^{1 (1 f} — f ^{1 (1} x dx v—f + 1 ^j< x ) ³ + 1

1 — } < , < 1

1 < , < 3 в

Аналогично, на выпуклой поверхности

(4.11)

дение при наращивании

( ф

I д

7

^- Ф 1

7

до нуля.

Очевидно, что во втором случае напряжения не перераспределяются после наращивания и равны напряжениям при нагреве со знаком “-”. Поэтому без ограничения общности достаточно рассмотреть лишь первый случай, когда напряжения в процессе роста будут определяться ф 1 , а остаточные образуются путем наложения напряжений в биметаллическом шаре, находящемся при температуре — ф} .

Вновь используя безразмерные критерии

а

V a =   , V a ^а _й

Ve (1 — Va )Ve (в — 1) + РЕ^ (49)

и нормируя напряжения на величину вогнутой поверхности будем иметь

, на

-+ VФ 1

a = -у 1

f

( в — 1) j

_ 1— П

, — (1 — x ) ³ dx . , ( f v (1 — x ) ³ + 1      v 1 f + 1

в, ) f Н—t dx - ^S f

1^j K'l x) + 1      K'l f + 1

1 — }<1

1 < , < ³3 в

(4.10)

=       ² V e ^{(1 — 2} ^ 1 ) ^{(1 —} V a )

^Va    V e (1 — в Х1 + ft ) + 2 в 1 (1 — 2 ft 1 ) ^{, (}4^.12)

— ₌ V_aФ^ , О„

г

^V V O \ I ° = = .J I

(13 № f(1 + f ) ³ — 1 f (1 + x ) ³ — 1& ^{( П A/)} V- ., + ■ -^j(1 + x )3 + 7 dx_

M f^

(l + f ) ^J + V

—

f ^{(1 + x ) 3 —n} n —W V dx

3    ^{(1 + f )3 — 1} f ^{(1 + x )3 — 1} ,1

^{( в + 2 П} '     .) . ■ “j(1 + x )³T^,

(1 — в )[ f ^{2 n} ’⁺⁽¹₃^{+ x )3} dx — f ²ⁿ ’ ⁺⁽¹₃^{+ f )3} ], ^ (1 + x )³ + v       (1 + f )³ + v^J

Таким образом, параметры v , V_a , V

a

3 в < , < 1

1 < , < 1 + f

(4.13)

³ в < , < 1

1 < , < 1 + f

(4.14) являют

ся критериями подобия и определяют термоупругие напряжения в растущем шаре. На рис. 4., рис. 5. показано распределение напряжений в растущем слое в зависимости от v и знака кривизны поверхности роста.

5. ОБСУЖДЕНИЕ РЕЗУЛЬТАТОВ

Анализ двухслойной модели позволяет выявить некоторые закономерности формирования термоупругих напряжений в непрерывно по-

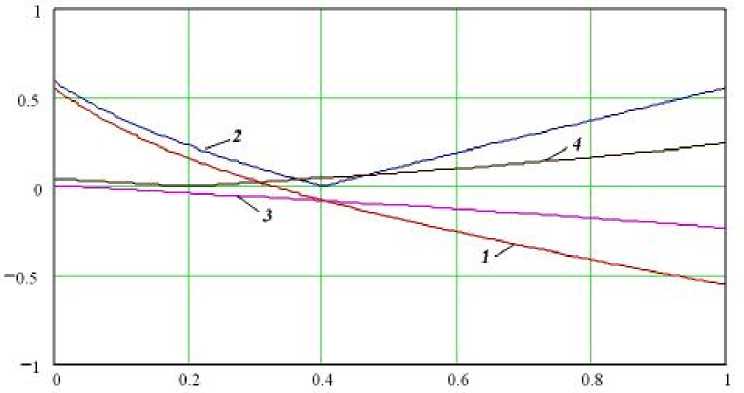
Рис. 4. Распределение окружной компоненты (1,3) и интенсивности температурных напряжений (2,4) в растущем слое на вогнутой поверхности: 1,2 – при x = 0.2 и n = -0.9; 3,4 – при x = 0.2 и n = 1.5

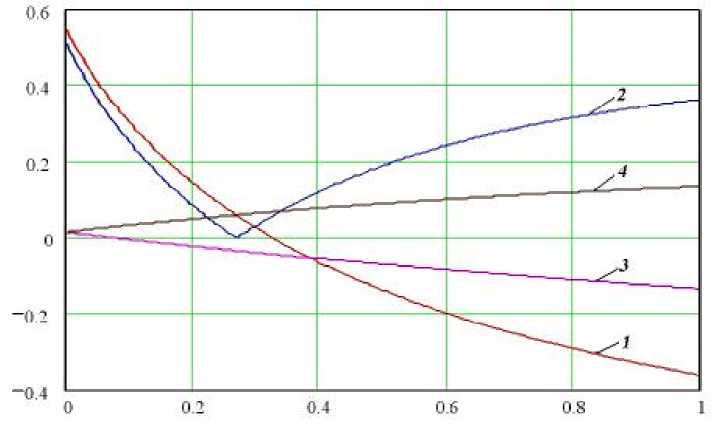
Рис. 5. Распределение окружной компоненты (1,3) и интенсивности температурных остаточных

напряжений (2,4) в растущем слое на выпуклой поверхности:

1,2 – при x=0.2 и n=-0.9; 3,4 – при x=0.2 и n= 0,5

слойно растущих телах, которые, как представляется, применимы и для тел с геометрией отличной от сферической:

вид распределения напряжений в послойно растущем теле определяется критерием подобия ν , имеющим смысл приведенной относительной жесткости основы;

наибольшая вариативность результирующих напряжений наблюдается в случае “твердый слой на мягкой оправке” ( V < - 0,5 ) при a 1 0 ( ψ _а <1 ) . В этом случае распределение температурных напряжений подобно кристаллизационным со знаком минус и тем самым компенсируют последние. При ψ _а >1 температурная компонента меняет знак и кристаллизационные напряжения напротив усиливают температурные. При этом знак радиальных напряжений соответствует знаку кривизны поверхности;

в процессах роста с преобладанием кристаллизационных напряжений для вышеуказанных систем существуют два характерных значения толщины слоя, при которых происходит смена знака окружных напряжений на границе с основой. Причем, чем выше относительная твердость слоя, тем меньше величины критических толщин;

знак температурной компоненты напряжений определяется разностью коэффициентов температурного расширения основного и растущего слоев, а наибольший диапазон возможного регулирования имеет место при a1a0 –совпадает по знаку с кристаллизационной.