Об одном методе вычисления обобщённых нормальных решений недоопределённых линейных систем

Недоопределённые системы линейных алгебраических уравнений (СЛАУ) возникают при решении различных прикладных задач, например, в сейсмической томографии [1], при обработке сигналов с утраченными фрагментами [2], при расчётах вариообъективов [3] и др.

Для нахождения нормального решения недоопределённых СЛАУ в настоящее время используются следующие подходы: методы, основанные на сингулярном разложении матриц ( SVD -разложение), методы нормальных уравнений и метод расширенных систем. Например, в работе [4] для решения разреженных недоопределённых СЛАУ с матрицами специальной структуры предложен параллельный алгоритм с использованием ортогональных разложений. Однако перечисленные методы не позволяют вычислять обобщённые нормальные решения, минимизирующие расстояние до произвольного априори заданного вектора («пробного» решения).

Для нахождения решений переопределённых разреженных СЛАУ большой размерности существует известный подход, основанный на использовании расширенных систем, который обладает рядом преимуществ [5]. Для недоопределённых разреженных СЛАУ большой размерности в настоящее время нет подхода, позволяющего вычислять обобщённые нормальные решения.

В статье предлагается новый метод нахождения обобщённых нормальных решений недоопределён- ных, возможно разреженных и плохо обусловленных, СЛАУ большой размерности на основе специальной расширенной системы.

1.    Метод расширенной системы

Рассмотрим недоопределённую СЛАУ

Au = f ,                                       (1)

где A e R m ^x n , u e R n , f e R m , m <  n , rank( A ) = m .

Необходимо вычислить нормальное решение u * относительно произвольного (априори заданного) вектора u 0 :

• u . = min I| u - u 0 11,                                            (2)

ueU где U = {ueRn: Au = f} - множество решений Au = f, uо 4 U, ||-|| = ||-||2 - евклидова векторная норма. В дальнейшем (2) будем называть обобщённым нормальным решением.

Известно [6], что решение задачи (2) имеет вид

• u . = A ⁺ f + ( I n - A ⁺ A ) u о ,                          (3)

где I n – единичная матрица порядка n , A ⁺ – псевдооб-ратная матрица Мура–Пенроуза матрицы A [5].

Однако, как отмечалось во введении, непосредственное нахождение псевдообратной матрицы, например, с помощью SVD -разложения, для разреженных матриц большой и сверхбольшой размерностей сопряжено со значительными вычислительными затратами.

Задача (2) также может быть решена на основе подхода, известного как вторая трансформация Гаусса.

По условию задачи имеем u е U и в соответствии с (2) ( и - и 0 ) ± ker A , из этого следует, что

(и - и0) е Im Aт ,(4)

или и = ATz + и 0.(5)

Подставив u в (1), получаем

A (ATz + и о ) = f(6)

или

AATz = f - Au0.(7)

Решая (6), находим вектор z = ( AA ^т ) ^-1 ( f - Au ₀). Подставив этот вектор в (5), получаем искомое решение u * .

Если вектор u 0 = 0 то из (3) следует, что u * = A ⁺ f .

Одним из главных недостатков при переходе к системе (7) является значительное увеличение спектрального числа обусловленности матрицы AA^T , так как

^(AA >=ц2 (A >=5и, где G1(A) и gm(A) - максимальное и минимальное сингулярные числа матрицы A, gm(A) > 0, так как rank (A) = m.

При больших числах обусловленности матрицы системы (6) имеет место численная неустойчивость решения задачи известными прямыми методами.

С другой стороны, в общем случае трудно предсказать степень разреженности матрицы AA ^т при её формировании. Как показано в [7], матрица AA ^т может оказаться сильно заполненной даже в случае, когда среднее число ненулевых элементов в строке матрицы A примерно равно m . Например, матрицы с такой структурой возникают в задачах реконструкции двухмерных изображений из проекций [8].

В данной работе для решения задачи (2) предлагается подход, основанный на использовании специальной расширенной системы.

Запишем уравнение (5) в виде и - ATz = и0. (8)

Тогда, объединяя уравнения (8) и (1), приходим к расширенной системе вида

A

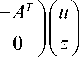
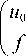
Заменяя в (9) z = – y , получаем её симметричную форму

I n A

AT

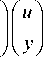
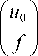
о B 9 = g ,

где

( \ \              | U |                                | U n |

B _€ R ⁽ n ⁺ m и n ⁺ m ) , 9 =     е R ^{n +} m , g = ⁰ _€ r ^{n +} m .

I y J            I f J

Утверждение 1. Решение системы (10) существует и притом единственно 9 » = ( и T , y Т ) T , где и * является решением (2), т.е. обобщённым нормальным решением.

Доказательство. Для доказательства этого утвер- ждения достаточно показать невырожденность матрицы B расширенной системы (10).

Покажем, что матрица B в расширенной системе (10) всегда невырожденная.

В [9] показано, что собственные значения X i ( B ) матрицы B равны

/ _ч — ±       + g²| , i = 1,2, ..., m ;         _ „

X i ( B ) = Ь 4 J,      , , , ’        (11)

• 1 1,    i = m + 1, . „ , m + n ,

где g i - сингулярные числа матрицы A , i = 1,2,..., m .

Так как rank ( A ) = m < n , все сингулярные числа матрицы A отличны от нуля, т.е. G 1 > ... >  g _m >0. Следовательно, все собственные значения X i ( B ) ^ 0, i = 1,2,..., m+n и det( B ) ^ 0. Таким образом, система (10) имеет единственное решение 9 » = ( и . ^т , y . ^т ) T . □

Из условия (4) следует, что to ( и - и ₀) e lm A ^T для любого to > 0. Тогда систему (10) можно представить в виде:

to I n

A

A^T j( и j

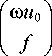
о B to 9 = g to

здесь

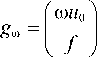
e R ^{( n + m} ) , to > 0.

Параметр to позволяет контролировать число обусловленности системы (12), что может быть использовано для повышения вычислительной устойчивости решения расширенной системы (12).

Покажем, что матрица B to при всех to > 0 невырожденная и, следовательно, система (12) всегда имеет единственное решение.

Утверждение 2. Решение системы (12) при любых to > 0 существует и притом единственно 9 » = ( и Т , y Т ) T .

Доказательство . Доказательство этого утверждения аналогично доказательству Утверждения 1.

Покажем невырожденность матрицы B to расширенной системы (12).

Сингулярные числа матрицы A отличны от нуля, G1 >... >gm>0, следовательно, все собственные значения Xi(B)^ 0, i = 1,2,..., m+n и равны x,( Bю) =

to

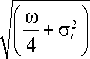
i = 1,2,. . , m ,

i = m + 1, . , m + n .

Таким образом, определитель матрицы Bш^0, из чего следует, что система (12) имеет единственное решение.

Рассмотрим возможные способы выбора параметра to в (12).

В работе [10] предложен способ выбора to , который минимизирует число обусловленности матрицы B to расширенной системы:

to = to = —j=c _m

( A ) ^« 2 ( B to) ~ V2 K ( A ) ,      (14)

Выбор единичного вектора в качестве вектора пробного решения u 0 – наиболее простой способ выбора вектора, отличного от нулевого и не принадлежащего области решений системы (15).

• 2.    Перевод вектора u * из вещественных чисел в целые (если необходимо).

2. Численные результаты

Рассмотрим следующее несбалансированное уравнение химической реакции

MnO- + H+ + Fe2+ ^ Mn2+ + H2O + Fe3+ , или в математической формулировке u1MnO- + u 2H+ + u 3Fe2+ = u 4Mn2+ + u 5H2O+u 6Fe3+. (17)

Для уравнения (17) матрица коэффициентов имеет вид где k2(Bto) - спектральное число обусловленности матрицы Bto расширенной системы (12), k2(A) - спектральное число обусловленности матрицы A исходной задачи (1).

r 1

- 1

- 1 0

- 2 0

0 - 1

(- 1 1

2 - 2

0 - 3 J

В качестве иллюстративного примера рассмотрим задачу балансировки химических уравнений, которая сводится к определению (целочисленных) стехиометрических коэффициентов (баланс масс). Следует отметить, что в зависимости от рассматриваемого химического процесса вычисление целочисленных стехиометрических коэффициентов требуется не всегда.

Современные подходы [11] для определения стехиометрических коэффициентов основаны на решении однородных недоопределённых систем линейных алгебраических уравнений вида

Au = 0, A e К ^{m x n} , u e R , m <  n , rank ( A ) = m . (15)

Здесь A – матрица коэффициентов химической реакции, u – вектор неизвестных целочисленных стехиометрических коэффициентов.

В дальнейшем будем полагать, что химические реакции возможны и имеют одну степень свободы. Это означает, что размерность пространства решений L = { u e R ⁿ : Au = 0} однородной СЛАУ (15) равна 1:

dim ( L ) = n - rank ( A ) = n - m = 1. (16)

Одним из недостатков известных методов решения задачи (15) является применение целочисленной арифметики, что значительно усложняет вычислительный процесс [12].

Задачу определения целочисленных стехиометрических коэффициентов с помощью специальной расширенной системы (9) можно разделить на следующие этапы [13]

1. Решение задачи u * = argmin | |u - u 0Ц, где u0 =(1,..., 1)т с использованием (9) при f= (0,..., 0)т.

Для нахождения стехиометрических коэффициентов уравнения (17) на первом этапе вычисляется обобщённое нормальное решение задачи (2) с помощью расширенной системы (9), где f = (0,..., 0) ^T e R ⁵ , u 0 = (1,..., 1) ^T e R ⁶ .

Решение (вещественное) u * системы (9):

r 0.181818181818182 ^

1.45454545454545

0.909090909090910

0.181818181818182

0.727272727272727

₍ 0.909090909090909 _?

Для перевода вещественных коэффициентов в целые воспользуемся стандартным подходом [13].

Окончательно получаем вектор целочисленных стехиометрических коэффициентов:

u = ( 1, 8, 5,1, 4, 5 ) ^T .

Таким образом, сбалансированное уравнение химической реакции имеет следующий вид

1 - MnO - + 8 ■ H ⁺+ 5 ■ Fe^{2 +} = 1 - Mn^{2 +}+ 4 ■ H ₂ O + 5 ■ Fe^{3 +} .

Заключение

В работе представлен новый метод вычисления обобщённых нормальных решений недоопределённых систем линейных алгебраических уравнений на основе специальных расширенных систем (9) и (12).

Для нахождения решений систем (9) и (12) могут применяться известные методы, основанные на LU- или QR -разложениях.

В случае плохой обусловленности матрицы A задачи (1), (2) для нахождения устойчивых решений на основе специальной расширенной системы (12) эффективно применять итерационное уточнение, аналогично задачам наименьших квадратов (с матрицей A полного столбцового ранга), предложенное в работе [9] Бьёрком (Å. Björck).

В работе [14] предложен новый алгоритм итерационного уточнения с предобуславливанием на основе метода обобщённых минимальных невязок (GMRES-IT) для очень плохо обусловленных разреженных линейных систем большой размерности. Данный подход можно эффективно использовать для решения очень плохо обусловленных и разреженных задач (1), (2) большой размерности на основе расширенной системы (12).