Об одном нелинейном интегро-дифференциальном уравнении

Одним из способов повышения точности описания процессов различной природы является учёт при протекании этих последних нелокальности взаимодействий [1; 2]. Однако комбинация нелинейности математической модели с простейшей нелокальностью в виде пространственного сдвига уже приводит к резкому возрастанию математических трудностей (см., например, [3]), поэтому поиск точно решаемых модельных примеров, обладающих как нелинейностью, так и нелокальностью, приобретает важное значение.

Рассмотрим следующее интегро-дифференциальное уравнение:

d u ( x , y , t ) ∂ t

xy

+ jju(x - %,y - n,t) u(^,П,t)' d^dn = 0,

в котором неизвестная функция u ( x , y , t ) определена в I-м квадранте: x >  0, у >  0 .

Снабдим уравнение (1) начальным условием:

и ( x , у ,0) = и ₀( x , у ) , x >  0, у >  0 ,

тогда для решения задачи Коши (1)-(2) справедлива следующая теорема.

Теорема. Пусть существуют такие константы М_о >  0 , h₀ >  0 и k₀ >  0 , что в I-м

квадранте функция (2) удовлетворяет неравенству:

I и 0 ( x , у ) 1 ^ M 0 • exp( hx + k 0 У ) ,

тогда точное решение задачи Коши (1)-(2) имеет вид:

а + i « b + i «     тт /      \                                      j 1

u ^{( x} , у , t ) = f j ^{0 p} , ^q    • ^exp⁽ p • ^x + q • у ) • ^p q ₂ ,

1 + 1 • U ( p , q )                      (2 • n • i )²

a - 1 co b - 1 w            0V-r’J/

где

+X+X

U э ( Р , q ) = f f и 0 ( x , У ) • exp( - p • x - q • у ) • dxdy ,

0 0

а в формуле (4) прямые Re p = а и Re q = b выбраны так, чтобы все особенности функции

U ₀( Р , q )/(1 + t ’ U ₀( Р , q )) в комплексных плоскостях p ид соответственно оставались

слева от них.

Доказательство. Нелинейный член в уравнении (1) представляет собой двойную свёртку лапласовского типа по обеим пространственным переменным, поэтому будем искать его решение с помощью двойного преобразования Лапласа ― и по x , и по y .

В рамках этого формализма переход от оригинала и ( x , у , t ) к изображению U ( p , q , t ) имеет вид [4]:

+И+И

U ( p , q , t ) = f f и ( x , у , t ) • exp( - p • x - q • у ) • dxdy , 0 0

а исходное интегро-дифференциальное уравнение (1) для оригинала трансформируется в обыкновенное дифференциальное уравнение для изображения (6):

^{d U (} p , q , t ) + U ²( p , q , t ) = 0 ,     U ( p , q ,0) = U 0 ( p , q ) .                        (7)

d t

Начальным условием для уравнения (7) является функция (5), причём условие (3)

является достаточным условием её существования в области Re p >  h₀ и Re q >  k₀ [4].

Задача Коши (7) имеет следующее точное решение:

U ( p , q , t ) =

^U 0 ⁽ p , q )

¹ + t • ^U 0 ⁽ p , q ) ,

а формула (4) представляет собой обращение двумерного преобразования Лапласа (6).

Однако формула (4), выражающая общее решение задачи Коши (1)-(2), неудобна для практического применения, поскольку для её использования надо проводить интегрирование в комплексном пространстве С ² . Гораздо проще находить точные решения задачи Коши (1)(2) в явном виде следующим образом: вычислить по формуле (5) изображение начального условия (2), а затем проверить по таблице двумерных преобразований Лапласа, приведённой в книге [4], соответствует ли изображение, найденное по формуле (8), какой-либо функции из этой таблицы.

Продемонстрируем применение этого приёма на примере.

Пусть начальное условие для уравнения (1) имеет вид:

u 0( x, y) = A • J0(2 7 а о xy),    x > 0, y > 0 , a 0 > 0,(9)

где J _o ( z ) — это функция Бесселя, тогда интеграл (5) от функции (9) легко вычисляется с помощью известного разложения функции J _o ( z ) в степенной ряд:

и0( p, q) = ~^~.(10)

pq + a 0

Подставляя выражение (10) в формулу (8), получим для изображения решения:

U (p, q, t) =-----A       .(11)

pq + a ₀ + At

Функция (11) получается из функции (10) заменой a ₀ ^ a ₀ + At , поэтому вследствие единственности обратного преобразования Лапласа по переменным p и q [4] оригинал для изображения (11) получается из функции (9) той же заменой:

u ( x , y , t ) = A • J₀(2j(a 0 + A1 ) xy ).                               (12)

При A > 0 функция (12) обладает колебательным характером. На рисунке 1 приведён график функции (9) при A = 1 и ао = 1 • С течением времени характерная «длина волны» уменьшается ― для этого достаточно сравнить рис. 1 с рис. 2, на котором представлен график функции (12) при тех же параметрах A = 1 и а0 = 1, но в момент времени t = 3. Если же A < 0 , то при tc = а0/| A | в решении (12) происходит переход от колебательного режима к режиму с неограниченно возрастающей по модулю функцией u(x, y,t) . С формальной точки зрения этот переход выражается в замене функции Бесселя Jo (z) на модифицированную функцию Бесселя Io (z) при t > tc. Рисунки 3 и 4 иллюстрируют этот эффект. В этом случае при t ^ tc - 0 характерная «длина волны» увеличивается, что приводит к уплощению графика функции (12) до тех пор, пока при t = tc он не становится плоскостью и (x, у, tc) = -|4|

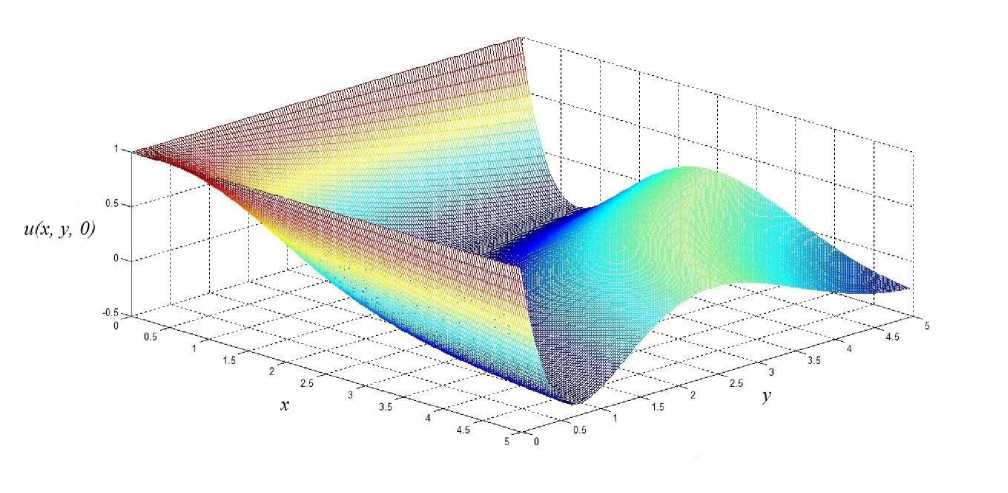
Рис. 1. График начального условия и(х,у, 0) уравнения (1) при А _о = 1 и а ₀ = 1.

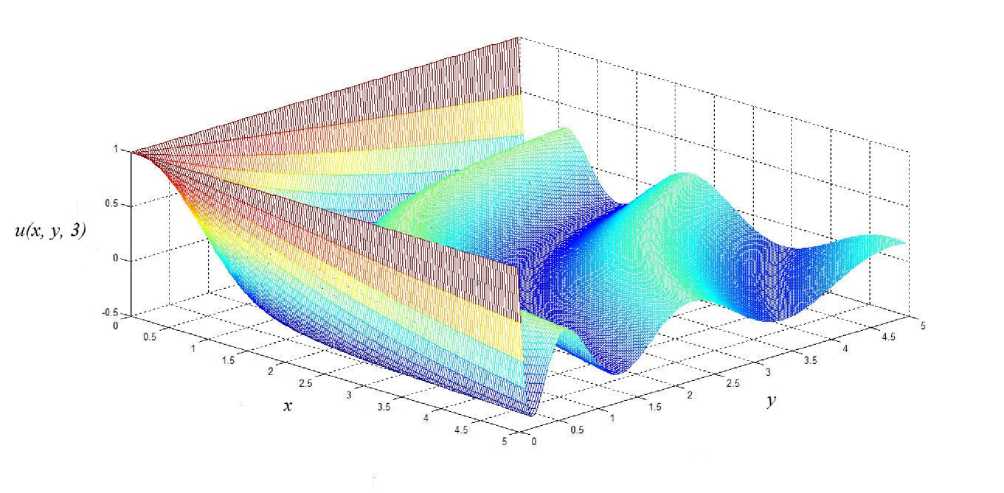
Рис. 2. График решения задачи Коши (1)-(2) при t = 3 , A = 1 и a ₀ = 1.

Таким образом, при переходе в решении (12) параметром A нулевого значения из ограниченного начального условия (9) за конечное время развивается неограниченное решение, то есть система (1) в своём поведении демонстрирует некоторое сходство с фазовым переходом второго рода [5] или с бифуркацией Андронова-Хопфа [6].

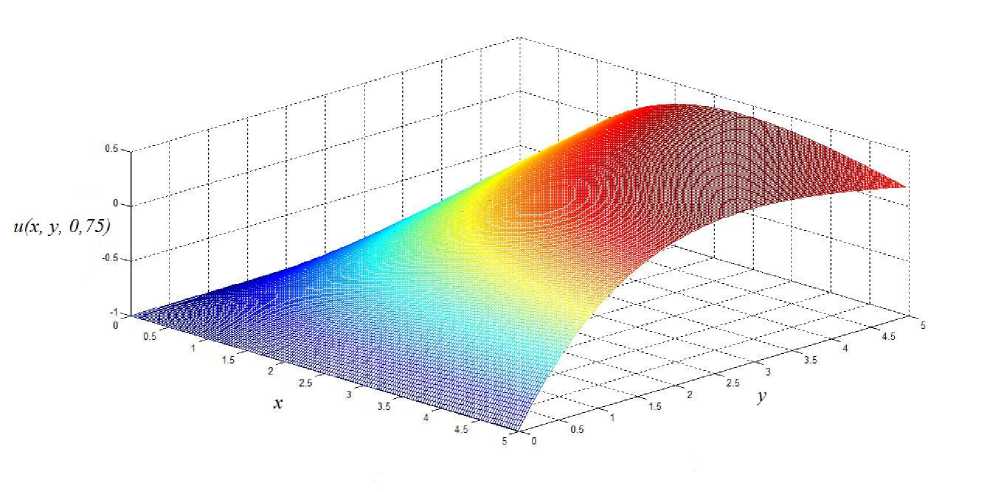
Рис. 3. График решения задачи Коши (1)-(2) при t = 0,75 и A = - 1 и а ₀ = 1.

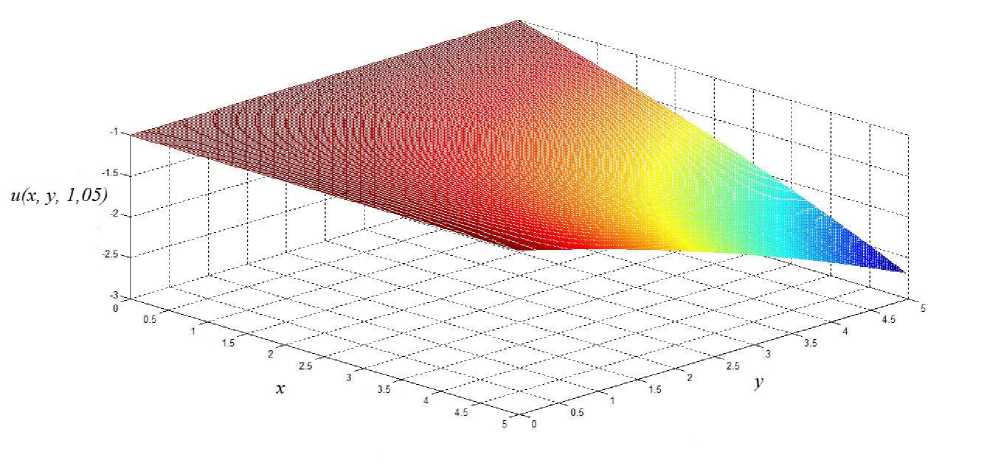
Рис. 4. График решения задачи Коши (1)-(2) при t = 1,05 и A = - 1, a₀ = 1.

В заключение необходимо отметить, что если точное решение u ( x , y , t ) задачи Коши (1)-(2) из каких-либо соображений известно, то двойная свёртка лапласовского типа начального условия (2) самого с собой может быть вычислена по формуле:

xy jj u0(x - %,У - п) u0(^П) • dd 0 0

d u ( x , у , t )

∂ t

t = 0

а при известной функции (5) применение двойного преобразования Лапласа по переменным x и y к левой части формулы (13) может привести к пополнению таблиц преобразований

Лапласа по двум переменным.

В частности, подставляя в соотношение (13) функции (9) и (12), найдём:

00                                              a^a 0

Наконец, с помощью выражения (10), взятого при A = 1, из формулы (14) без вычислений можно получить, что:

+∞+∞

⁽ pq + ^a 0 ⁾²

Ui “ • J 1 (2V a 0 xy ) ■ exp( - p • x - q ■ У ) ■ dxdy = 0 0 V ^a 0