Об одном новом методе электроакустического преобразования. Теория, основанная на электрокинетических явлениях. Ч. I. Гидродинамический аспект
Автор: Сергеев В.А., Шарфарец Борис Пинкусович
Журнал: Научное приборостроение @nauchnoe-priborostroenie
Рубрика: Физика приборостроения
Статья в выпуске: 2 т.28, 2018 года.
Бесплатный доступ
В качестве основной физической модели нового вида электроакустического преобразования предлагается использовать теорию такого электрокинетического явления, как электроосмос. Приводятся основные детали теории преобразования и связанных с ним гидродинамических и электрических параметров. Рассматривается гидродинамика стационарного электроосмотического движения жидкости в капилляре. Приводятся выражения для скоростей потоков в условиях наличия суммарного течения двух потоков: течения Пуазейля и элетроосмотического течения. Приводится также обобщение гидродинамики электроосмотического потока на произвольную капиллярно-пористую среду. Акустические аспекты теории предполагается рассмотреть во второй части настоящей работы.
Электроакустическое преобразование, электрокинетические явления, гидродинамика электроосмоса, капиллярно-пористые среды, электроосмотическая скорость
Короткий адрес: https://sciup.org/142214851
IDR: 142214851
Текст научной статьи Об одном новом методе электроакустического преобразования. Теория, основанная на электрокинетических явлениях. Ч. I. Гидродинамический аспект
Сравнительно недавно появилось изобретение [1] нового вида акустического преобразователя, основанного на совершенно новом принципе. Его описание дано в Приложении 1.
Авторы назвали описанный эффект "туннельным кинетическим эффектом". Смысл формулы изобретения, таким образом, сводится к тому, что внешнее статическое электрическое поле, промо-дулированное звуковой составляющей, трансформирует изначально пористый рабочий элемент путем формирования "кинетических туннелей (микроканалов)". В рабочем элементе внутренние микроканалы согласованно ориентируются по линиям векторного поля электрической напряженности. При этом микроканалы имеют поперечный размер, соизмеримый с размером молекул внутренней газовой среды. Это в свою очередь сокращает число степеней свободы молекул газовой среды с трех до единицы, а это при условии сохранения кинетической энергии молекул газа увеличивает скорость перемещения молекул вдоль микроканалов. Таким образом, электрическое поле воздействует только на рабочий элемент, образуя и спрямляя микроканалы в нем, а уже это в свою очередь влияет на скорость молекул внутренней газовой среды.
Описанная модель, по мнению авторов, относится к разряду феноменологических,1) т. к. физика самого процесса остается нераскрытой, а потому может подвергаться сомнению.
Поведение газовой среды рассматривается в рамках кинетической теории газов, в то время как акустические эффекты обычно рассматриваются в рамках теории механики сплошных сред. Кроме того, в предложенной теории совершенно не учитывается такое широко известное электро-кинетическое явление, как электроосмос, возникающее в случае приложения электрического потенциала к средам, где существуют границы раздела фаз между твердыми и жидкими (газообразными) фазами. На границах фаз обычно образуется двойной электрический слой (ДЭС), в котором нарушается электронейтральность жидкости (газа), что приводит собственно к явлению электроосмоса, выражающемуся в движении жидкости под воздействием стационарного электрического поля. Кроме того, отсутствие математических моделей физического процесса не позволяет его количественно оценивать, а следовательно, прогнозировать явление при изменении независимых параметров модели.
В этой связи представляется целесообразным действовать в рамках разумного принципа бритвы Оккама: "Не следует множить сущее без необходимости". Поэтому в настоящей работе делается попытка объяснить описанные в патенте происходящие физические процессы прежде всего в рамках уже известной физической теории электроосмоса с помощью испытанного метода сравнения теории и эксперимента. Это и является основной целью работы.
КРАТКАЯ ТЕОРИЯ ЭЛЕКТРООСМОСА
Понятия теории
Теория электроосмоса берет свое начало с опубликования в 1809 г. результатов известных опытов профессора московского университета Ф.Ф. Реуса. К настоящему времени теория электроосмоса устоялась и опубликована в солидном количестве источников, из которых упомянем [2–4].
В настоящей работе приводятся необходимые детали теории электроосмоса; путем сопоставления теории и эксперимента проверяется адекватность электроосмотической теории приведенному в патенте электроакустическому преобразованию. Устанавливаются основные параметры, определяющие эффективность электроакустических преобразований предложенного устройства.
Ниже приведены основные определения и уравнения, используемые в теории электроосмоса. Материалы цитируются (если не оговорено противное) по обзорной работе [5], основанной на содержании работ [2–4].
Электрокинетические явления — совокупность явлений, происходящих в системах, содержащих капилляры или мембраны, размещенные в электролите, при наложении электрического поля, и обратных им эффектов [6, с. 534]. К электро-кинетическим эффектам, в частности, относится электроосмос . Основную роль в электрокинетиче-ских явлениях играет ДЭС, формирующийся на границе раздела фаз (одна из которых должна обязательно быть жидкой или газообразной), и его поляризация.
Электроосмос — это движение жидкости (газа) через капилляры или пористые диафрагмы при наложении внешнего электрического поля.
Двойной электрический слой (ДЭС)
В силу различных причин на поверхности раздела твердой и жидкой (газообразной) фаз образуется ДЭС (см., например, [2, гл. 1, 3, 7]). Он образуется безотносительно к тому, присутствует или нет внешний электрический потенциал. Строение ДЭС показано на рис. 1. Твердая фаза находится
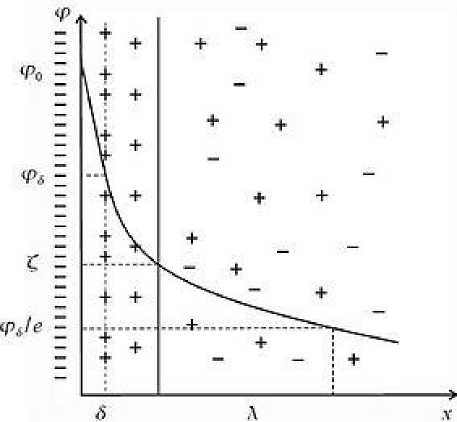
Рис. 1. Распределение электрического потенциала ϕ в ДЭС в зависимости от расстояния до границы фаз; ϕ 0 — потенциал на границе фаз; δ — толщина первого слоя противоионов; ϕδ — электрический потенциал на расстоянии δ от границы; ς — значение потенциала на поверхности скольжения; λ — длина Дебая, равная фактически толщине ДЭС; x — расстояние от границы фаз.
(Воспроизведено по URL:
слева от оси ϕ , справа вдоль оси x находится жидкая (газообразная) фаза.
На поверхности твердой фазы образуется слой (очень тонкий, имеющий молекулярные размеры) потенциалопределяющих ионов. Они как бы припаяны к твердой границе. Все эти ионы одного знака (на рисунке на межфазной границе они помечены знаком "-")2).
Вследствие законов электростатики противоионы в жидкости (со знаком "+") при контакте с твердой фазой начинают притягиваться к твердой границе; ионы жидкости, заряженные одноименно заряду границы (коионы со знаком "-"), отталкиваются от границы. Часть противоионов остаются неподвижными даже при движении жидкости. Это адсорбционная плотная, неподвижная часть ДЭС. Остальные противоионы и коионы остаются подвижными и образуют диффузную (подвижную) часть ДЭС. По схеме Штерна—Грэма [7, с. 143] адсорбционная часть ДЭС может состоять из внутренней и внешней частей. Внутренняя часть, расположенная у границы раздела фаз (на рисунке интервал x е[0,5 ]), образована специфически адсорбирующимися на данной поверхности ионами (внутренняя плоскость Гельмгольца). Внешнюю часть адсорбционного слоя составляют ионы, проявляющие не столь сильно свойство адсорбции, как ионы из внутреннего слоя (на рисунке интервал x е [5, вертикальная сплошная линия]).
Область, где касаются адсорбционный и диффузный слои, называется поверхностью скольжения , которая получается несколько отодвинутой от реальной границы (на рисунке поверхность скольжения обозначена вертикальной сплошной линией). Диффузный слой простирается от плоскости x = 5 до правого вертикального пунктирного отрезка на рис. 1 и имеет толщину, равную дебаевской длине (см. ниже). Подвижная часть ДЭС за небольшое время переходного процесса приходит к стационарной концентрации. Это является следствием того, что при большой концентрации ионов одного знака они начинают отталкиваться друг от друга, кроме того имеет место так называемый электрохимический потенциал жидкости. Результатом действия этих причин является то, что концентрации противоионов и коионов в ДЭС и значение образовавшегося распределения электрического потенциала в ДЭС связаны между собой хорошо известным в физике распределением Больцмана (это привычная экспоненциальная зависимость, стремящаяся к константе) [2, с. 15], [5, выражение (8)].
Таким образом, структуру ДЭС в жидкой фазе составляет два слоя:
– слой Гельмгольца (адсорбционная (плотная, неподвижная) часть ДЭС), примыкающий непосредственно к межфазной поверхности;
– диффузный слой, в котором в жидкой фазе присутствуют ионы обоих знаков, противоионы (+) и коионы (-), однако доминируют в нем противоионы, т. е. ионы, заряженные противоположно заряду поверхности твердой фазы; толщина диффузного слоя λD называется дебаевской длиной (выражение для дебаевской длины приведено ниже).
Электрической характеристикой ДЭС является потенциал вектора электрической напряженности ϕ . Выделяют несколько характерных потенциалов (см. рис. 1):
– потенциал жидкости на границе фаз ϕ 0 ;
– потенциал внутренней части адсорбционного слоя ДЭС ϕδ . Внутри диффузного слоя потенциал можно рассчитывать по формуле Гуи—Чепмена
x
Ф = Ф5е ' ;
- потенциал диффузного слоя фх = А , меньший, чем ϕδ , в e раз и характеризующий толщину диффузного слоя;
– электрокинетический потенциал или дзета-потенциал ( ς -потенциал).
Последний соответствует плоскости скольжения, которая образуется в результате того, что ионы, находящиеся левее нее (сплошной вертикальной прямой на рис. 1), не участвуют в движении при приложении внешнего электрического поля, оставаясь неподвижными. Оставшаяся правее плоскости скольжения часть диффузного слоя не является электронейтральной, что в конечном итоге и приводит к движению жидкости под воздействием стороннего электрического поля, т. е. к явлению электроосмоса. ς -потенциал является одной из важнейших характеристик ДЭС.
УРАВНЕНИЕ ПУАССОНА
Вектор напряженности электрического поля E для условий электростатики является потенциальным
E = -V ф , (1)
где ϕ — скалярный потенциал вектора E . Тогда при заданном распределении свободных зарядов потенциал электростатического поля в однородном изотропном диэлектрике удовлетворяет следующему уравнению Пуассона
А ф = - (в СИ),
εε 0
А ф = - 4 ^ - (в СГСЭ). ε
Здесь s0 = 8.85-IO-12 Кл2/(Н- м2) = 8.85-10-12 Ф/м — электрическая постоянная; ε — относительная диэлектрическая проницаемость среды, показывающая во сколько раз сила взаимодействия между двумя постоянными зарядами в данной среде меньше, чем в вакууме; ϕ — скалярный по- dq тенциал; р, = — — объемная плотность элек-el dV трического заряда (заряд единицы объема); dq — величина заряда, сосредоточенного в объеме dV .
В общем случае уравнение Пуассона (2) оказывается нелинейным и, как правило, трудно разрешимым. Однако в случае выполнения приближения Дебая—Хюккеля, когда тепловая энергия превосходит электрическую энергию [3, с. 97], [4, с. 147]
Zee, « k B T , получают линеаризованное приближение уравнения (2) в виде уравнения Дебая—Хюккеля
A ф ( r ) = ТГ ф ( r ) . (2а)
λD
Здесь приняты обозначения: Z — заряд иона в единицах заряда протона (безразмерная величина, равная валентности иона с учетом знака его избыточного заряда); kB = 1.3806488 - 10 - 23 Дж/Кл — постоянная Больцмана; T , К — абсолютная температура; e = 1.602176565 - 10 - 19 Кл — элементарный электрический заряд (заряд протона); ς — дзета-потенциал (см. рис. 1); λD — длина Дебая (дебаевская длина или радиус экранирования), определяемая выражением [3, с. 97], [4, с. 147]
_ = ее о k B T
D" 2(Z (Ze )2 c о, где c0 — равновесная концентрация ионов вне ДЭС.
Отметим, что решение ф ( г ) , полученное из уравнения Дебая—Хюккеля (2а), позволяет рассчитать объемную плотность электрического заряда ρ el из уравнения (2), например, в СИ в виде
P el = - ее о А ф .
УРАВНЕНИЕ НАВЬЕ—СТОКСА
ПРИ ВОЗДЕЙСТВИИ РАЗЛИЧНЫХ ВНЕШНИХ СИЛ, ВКЛЮЧАЯ ЭЛЕКТРИЧЕСКОЕ ПОЛЕ
Общий случай
Закон сохранения импульса при движении вязкой несжимаемой жидкости в поле силы тяжести при наличии внешнего электрического поля с напряженностью E ext , а также в поле давления в дифференциальной форме записывается в виде уравнения Навье—Стокса (см., например, работы [3, с. 309], [4, с. 141], [5] и др.)
P ^ + ( v -V ) v ) = -V p + П A v + P g + P el E ext . (3)
Здесь
v
,
p
— поля векторов скорости и давления в жидкости;
ρ
— плотность жидкости;
g
— вектор ускорения силы тяжести (в декартовой системе координат с осью
z
, направленной вертикально вверх, вектор
g =
(
0,0,
-
g
)
,
g
— ускорение силы тяжести);
η
— динамическая вязкость среды.
К уравнению движения (3) необходимо дописать уравнение непрерывности для несжимаемой жидкости [8, с. 37]
V-
v
=
0. (3а)
Рассмотрим решения уравнений (3), (3а) для трубы в виде прямого кругового цилиндра в некоторых частных случаях применительно к рассматриваемой тематике. Течение Пуазейля
Это одно из самых простых
точных решений
уравнения Навье—Стокса (3). Так называют установившееся (стационарное) течение вязкой несжимаемой жидкости с постоянной вязкостью в цилиндрической трубе произвольного сечения или между двумя параллельными плоскостями под действием
постоянной
разности давлений. Это означает, что для такого течения третье и четвертое слагаемые в правой части (3) приравниваются к нулю. Пусть скорость жидкости в цилиндре имеет только
z
-составляющую
v
=
(
0,0,
v
z
)
, в случае цилиндрической трубы направленную вдоль оси
z
. Тогда уравнение непрерывности (3а) выполняется тождественно, а уравнение (3) сводится к скалярному виду для компоненты
vz
[8, с. 81]
1 5 1 d ) A ^ vz = - . rT I vz r Cr V cr J
1 d
p η
d
z
откуда из постановки задачи следует, dP a Ap что — = const = —, где Ap — разность давлений dz l на концах трубы, а l — ее длина. В (4) опера- тор A^
p2
d
2
)
'
Vd
x
о
y
J
— поперечный оператор Ла- пласа. Интегрирование последнего уравнения дает для vz [8, с. 82]
v
z
=Tp
(
R
2 -
r1
)
■ (5) 4
ηl
Здесь
R
— радиус трубы;
r
— текущий радиус. При интегрировании уравнения (4) учитывалось условие прилипания на границе
r
=
R
. Таким образом, скорость в сечении трубы распределена по параболическому закону, оставаясь постоянной по длине трубы (рис. 2).
Замечание.
Для течений в прямых трубах закон (5) выполняется при ламинарном течении жидкости, если число Рейнольдса Re
<
1700, и обычно не выполняется при Re
>
104, т. е. при турбулентном ее течении [9, с. 57]. На рис. 2 показаны профили течений Пуазейля при ламинарном и турбу-
а б
Рис. 2.
Профили течений Пуазейля при ламинарном (а) и турбулентном движении (б).
(Воспроизведено по URL:
v
=
0.
z r
=
a
Решение задачи (6), (7) приведено, например, в работах [3, с. 220], [4, с. 161], однако здесь представляем его в нотации обзорной работы [5], более привычной для русскоязычных читателей: εε z ext, z ς
,
η
( V — I0 (r 1 Ad)
1
0
(
a
/
A
d
)
J
Здесь
I
0 — модифицированная функция Бесселя первого рода нулевого порядка.
Величина лентном движении, при котором течение уже перестает быть параболическим по профилю. ЭЛЕКТРООСМОТИЧЕСКОЕ ТЕЧЕНИЕ ЖИДКОСТИ Скорость течения При рассмотрении электроосмотического течения в уравнении (3) пренебрегают справа силами -Vp и pg . При этом слева в силу предположения о стационарности процесса во времени пропадает dv член p—, а также член p( v-V)v в силу предпо-51
ложения малости числа Рейнольдса Re
^
1, что означает справедливость оценки
| p
(
v
-V
)
v|
« |
n
A
v|
,
p( v -V) vz т. к. —------— « Re ^ 1 [8, с. 89] (вновь рассмат- ПА vz ривается движение жидкости в прямом круговом капилляре с осью, совпадающей с осью Oz). Пусть вектор Eext зависит только от координаты z (Eext = Eext, zez, ez — единичный орт вдоль оси z). Запишем с учетом сделанных замечаний уравнение (3) для случая стационарных (не зависящих от времени t) полей p и v . При этих условиях z -компонента уравнения (3) принимает вид п 9 Г 9 А
П
— I
Г
~ I
v
+
РEext Z
=
0. (6)
z
el ext,
z
r 9 r V 9 r )
К уравнению (6) необходимо добавить краевое условие на боковой границе капилляра, заключающееся в том, что на внешней границе слоя Гельмгольца (на поверхности скольжения) электроосмотическая скорость равна нулю. Обозначая через
a
(
a
<
R
) радиус поверхности скольжения, имеем
U
=
E
t ^0-
q
eo ext,
z
η
называется электроосмотической скоростью. Это выражение называется формулой Гельмгольца— Смолуховского. Известно, что при выполнении соотношения
A
d
^
a
(дебаевская длина много меньше радиуса капилляра) практически для всех
r
e
[
0,
a
)
будет справедливо соотношение
v
z
(
r
)
~
U
e
o
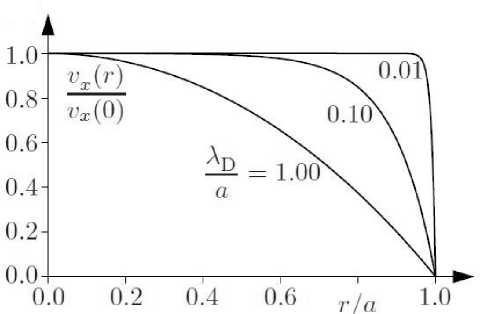
. Так, на рис. 3 для
A
d
I a
=
0.01 при
r
e
[
0,
~
0.98
a
]
справедливо
v
z
(
r
)
=
U
eo (на заимствованном рис. 3 [4, с. 162] электроосмотическая скорость обозначена
vx
(
r
)
), для
A
d
I a
=
0.10 при
r
e
[
0,
~
0.6
a
]
справедливо
v
z
(
r
)
=
U
eo, тогда как для
A
d
I a
=
1 характер распределения скорости
v
z
(
r
)
напоминает параболический профиль.
В [4, с. 158] вводится понятие
идеального электроосмотического течения,
определяемого четырьмя условиями:
Рис. 3.
Профили электроосмотической скорости. Первоисточник [4, с. 162].
–
ς
-потенциал постоянен на поверхности трубы (или плоской стенки для плоской поверхности);
– электрическое поле однородно;
– поток жидкости стационарен;
- выполняется условие
X
D
^
а
(для плоского
h
канала: XD ^ —, где h — расстояние между стен ками канала). Противоток течения Пуазейля и электроосмотического течения
Можно показать, что различные объемные силы справа в (3) могут при определенных условиях вызывать противоточные течения. Например, при постоянном градиенте давления возникает течение Пуазейля, а при наличии еще и электрической объемной силы возникает электроосмотическое течение. При этом в области малых чисел Рейнольдса в стационарном случае решение следует из одного и того же линеаризованного уравнения Навье—Стокса, которое для
z
-составляющей в цилиндрических координатах можно записать,
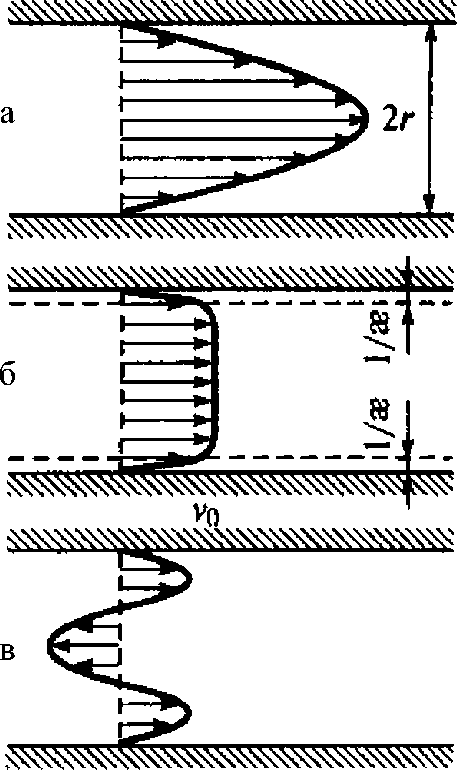
Рис. 4.
Сложение потоков.
Течение Пуазейля (а), электроосмотическое течение (б), их сумма в условиях противотока (в). (Воспроизведено по [7, рис. IV-10]) объединяя уравнения (4) и (6), так:
1
д
r
д
r
д) r— I v d r J
1
(
d
p
П
V
dz
ρ
el
E
ext,
z
Таким образом, решение
vz
будет суммой электроосмотического течения и течения Пуазей-ля. При разнонаправленности объемных сил, очевидно, возникает противоток течений. Направленные в противоположном направлении потоки жидкости складываются. На рис. 4 показаны течение Пуазейля (а), электроосмотическое течение (б) и их сумма в условиях противотока (в) (величина 1/æ на рисунке (б) равна дебаевской длине
λD
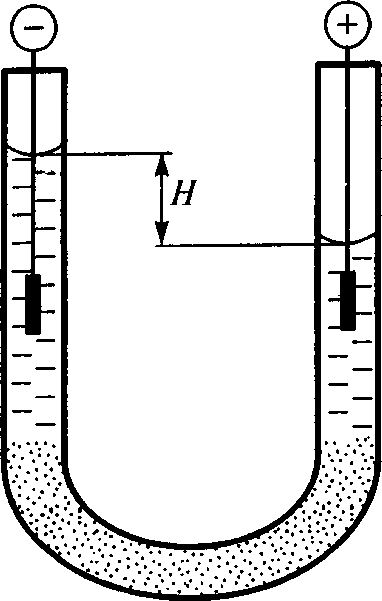
; величина æ — обратная величина ионной атмосферы). Как видно (рис. 4, в), в этом случае у стенок капилляра течение направлено в противоположную сторону, чем в его срединной части. При определенных условиях потоки течений могут компенсировать друг друга, и суммарный поток жидкости через сечение трубки может стать равным нулю. Именно этим можно объяснить тот факт, что при постановке Реусом опытов, повлекших открытие электроосмоса, устанавливалась постоянная разница уровней жидкости в ветвях U-образной трубки (см. рис. 5). Электроосмос приводит к изменению уровня жидкости в сообщающихся сосудах — анодной и катодной частях U-образной трубки. Этот эффект, называемый электроосмотическим поднятием, может оказаться сильным; например, приложение напряжения 100 В
Рис. 5.
Явление электроосмоса.
(Воспроизведено по [7, рис. IV-2]) может вызвать возникновение разности уровней до 20 см [7, с. 168].3)
Формализуем этот процесс, взяв за основу
z
-компоненту уравнения (3) и приняв во внимание только две объемные силы
ρ
g
и
ρ
el
E
ext . Тогда в стационарном случае получаем уравнение, аналогичное (10):
1 5^5) 1, „ z ~ —I r^ Iv^ = “(-Pg - PelEext,- ). r 5 r V 5 r J n
Член
ρg
связан с изменением гидростатического давления
p
st [8, с. 20]
p
st
= -
pgz
+
const,
5p t откуда -Vp t =--st- = pg. После чего уравнение st 5z (11) записывается в виде 1 _5_
r
5
r
5
P
st
— η
5
z
ρ
el
E
ext,
z
Уравнение (12) описывает наличие течения
5P t
Пуазейля с силой —st- и с разницей давлений Ap 5z на отрезке H = |Az | = |z 2 — zj, равной
|A
p
| =
pg
|A
z
| =
pgH
, и электроосмотического течения с объемной силой
—
p
el
E
ext
z
. Установивший-
ся уровень поднятия жидкости определяется из условия равенства нулю суммарного потока жидкости
Q
в капилляре:
Q
=
Q
E
+
Q
P
, где
Q
E
и
QP
— потоки жидкости в электроосмотическом течении и в течении Пуазейля соответственно. Эти величины равны:
QE
=
nR
2
^^
0
^
^
ext
[7, с. 184]
E
ηH
_ nR4 Ap и Qp =--[7, с. 182]. Здесь A^ — разность P 8η H ext потенциалов внешнего поля Eext,z на отрезке H ; R — радиус капилляра. Баланс этих потоков приводит к выражению для высоты поднятия жидкости H0 [7, с. 184] Hо =
8
εε
0
ς ρgR
2
A
^
ext
3) Вот как в работе [7, с. 184] об этом сказано: "Если перетекание среды приводит к появлению разности уровней в соединенных капилляром сосудах, то под действием возникающего при этом перепада давлений
A
p
=
p
g
A
H
возникает противоток ... среды, так что устанавливается распределение скоростей, как показано на рисунке".
Величина
H
0 получена для вертикальной ориентации капилляра. Аналогичные рассуждения требуется провести и для наклонного положения капилляра с той разницей, что необходимо в этом случае искать баланс проекций соответствующих потоков на направление оси
z
. При горизонтальной ориентации трубки поток жидкости будет непрерывным, т. к. не зависит от силы тяжести и потому течение Пуазейля, вызванное силой тяжести, будет отсутствовать.
Обобщение на произвольные пористые структуры Хотя формула (9) в теории электроосмоса была выведена для единичного прямого кругового и плоского капилляров, многочисленные исследователи использовали ее при изучении электроки-нетических явлений в пористых диафрагмах на том основании, что пористое тело можно уподобить системе капилляров. Возможность дальнейшего обобщения формул электроосмоса на случай течений со все возрастающей сложностью геометрии поверхности обусловлена фундаментальными особенностями этого вида гидродинамического течения вязкой жидкости [2, с. 10]. Оказалось, что эта теория обобщается не только на капилляры произвольной формы. В работе [2, § 2.2] рассмотрена система уравнений электроосмотического течения применительно к капиллярно-пористой системе со сколь угодно сложной геометрией внутренней поверхности, но при следующих принятых ограничениях:
– толщина двойного слоя достаточно мала, а радиусы кривизны внутренней поверхности больше некоторой величины, значительно превышающей величину дебаевской длины
λD
;
– минимальный линейный размер пор существенно превышает дебаевскую длину
λD
.
Совокупность этих ограничений позволяет рассматривать двойной слой на любом участке внутренней поверхности локально как плоский и достаточно тонкий и использовать формулу (9), при применении которой, однако, надо учитывать, что значение тангенциальной составляющей E(5)ext электрического поля Eext является функцией координат R — радиуса-вектора данного участка двойного слоя vs ( R ) = ^ ESje. ( R ).
При сложной геометрии капиллярно-пористого тела практически невозможно найти как распределение скоростей жидкости
v
, так и распределение электрического поля. Однако устанавливается по-
добие между этими величинами [2, с. 38]:
V
(
r
)
=
ff
0
£
E
ext
(
r
)
. (13)
η Характерным скоростям электроосмоса соответствуют малые значения чисел Рейнольдса, вследствие чего приходится использовать гидродинамику вязкой жидкости, течение которой, как правило, не потенциально в отличие от течений при больших числах Рейнольдса. Однако электроосмотическое течение отличается особыми граничными условиями на границе фаз. Если обычно течение вязкой жидкости характеризуется условием прилипания на границе (вектор скорости на границе зануляется), то при электроосмосе скорость вблизи границы пропорциональна градиенту электрического потенциала, если последний удов- летворяет граничному условию
Mxt
d
n
=
0
S на по- верхности раздела фаз S . Это обусловливает за- мечательную простоту гидродинамики электроосмоса — течение вязкой жидкости при малых числах Рейнольдса оказывается в данном случае потенциальным [2, с. 38].
Сложное распределение электрического поля и гидродинамической скорости в порах, фигурирующее в выражении (13), не доступно экспериментальному измерению. Доступная же экспериментальному измерению зависимость получена путем усреднения этой формулы по макроскопическому сечению капиллярно-пористого тела. Пусть d
s
— элемент сечения пор, перпендикулярного направлению приложенного электрического поля
E
ext . Интегрирование по суммарному сечению пор
Sn
, нормальному к
E
ext , приводит (13) к виду [2, с. 38]
J
vn ds
=
J
i
n
d
s
. (14)
ηK Sn Sn
Здесь
vn
— нормальная составляющая осмотической скорости
v
, совпадающая по направлению с вектором
E
ext ;
in
— нормальная составляющая тока, вызванная полем
E
ext ;
K
— удельная электропроводность среды.
Выражение (14) переписывается в виде [2, с. 38]
Veo
=
£££ I ηK
,
где
V
eo
=
J
v
n
d
s
— объемная скорость электроос-
S мотического течения при силе тока I = J in ds.
S
n
Отношение Veo / I , называемое электроосмоти- ческим переносом, доступно экспериментальному измерению и, согласно выражению (15), несет информацию об электрокинетическом потенциале ς [2, с. 39]. Вопросы, касающиеся различных аспектов пористых сред, частично отражены в Приложении 2. Характерные значения электоосмотических величин В работе [4, с. 159] даны следующие характерные значения: q = 0.1В; Ueo = 0.01м/с; ^eo = Ueo = ££^ ~ 7 • 10-8м/(В • с), где Дю — элек-Eext η троосмотическая подвижность. Дебаевская длина λD может достигать 1 мкм [3, с. 226]. При относительной диэлектрической проницаемости £ = 78.3 (у воды £ = 81), вязкости п = 0.89 -10-2 г/(см • с) (равно вязкости воды при температуре 25 ºС ) и Eext = 10 В/см электроосмотическая скорость равна Uo = 7.8 •10-5м/с [3, с. 219]. ВЫВОДЫ В работе предлагается в качестве основной физической модели нового вида электроакустического преобразователя использовать теорию такого электрокинетического явления, как электроосмос. Приводятся основные детали его теории и связанных с ним гидродинамических и электрических параметров. Рассматривается гидродинамика стационарного электроосмотического движения жидкости в капилляре. Приводятся выражения для скоростей потоков в условиях наличия суммарного течения двух потоков: течения Пуазейля и элетроосмотического течения. Приводится также обобщение гидродинамики электроосмотического потока на произвольную капиллярно-пористую среду. Акустические аспекты теории будут рассмотрены во второй части настоящей работы. ПРИЛОЖЕНИЕ 1 Описание из [1]: "Под действием напряжения, прилагаемого к рабочим обкладкам преобразователя, между ними возникает электрическое поле, которое воздействует на рабочий элемент и газовую среду, расположенную в теле рабочего элемента. В результате данного воздействия в теле рабочего элемента происходит формирование кинетических туннелей, в которых осуществляется преобразование векторов скоростей и внутренней кинетической энергии газовой среды в требуемом направлении. Диаграмма направленности излучаемого сигнала в основном определяется топологией внутренней структуры рабочего элемента и заданной конструкцией преобразователя. Коэффициенты преобразования кинетических туннелей (векторов внутренней кинетической энергии рабочей среды) являются функцией от напряженности электрического поля, прикладываемого к рабочему элементу. Изменяя напряженность электрического поля в соответствии с заданным сигналом, получаем ускоренное, направленное движение газовых молекул в требуемом направлении, которые, взаимодействуя с окружающей средой, возбуждают в ней акустические колебания". Приложение 2 Приведем необходимые определения (см., например [10], где выписана необходимая библиография). Пористые среды.
Важной характеристикой пористой среды является
пористость (porosity) m
, равная относительной объемной доле порового пространства в материале. Так, если в случае однородного пористого материала объемом
V
объем пор составляет
Vp
, то пористость этого образца равна
V m = ^. (П1)
Пористость является безразмерной величиной со значениями в интервале
m
е
[0,1].
Характерный размер пор d
.
В реальных пористых средах размеры пор распределены случайным образом. Поэтому введение характерного размера может быть произведено неоднозначно, однако определение такой величины бывает удобно для проведения оценок по порядку при анализе уравнений.
Просветность (surfaceporosity)
.
Если сделать мысленный поперечный разрез образца пористой среды, то в образовавшемся сечении площадью
S
часть площади
Sp
будет приходиться на поры. Отношение
S n = Sr (П2) называется просветностью. Величина просветно-сти зависит от характера разреза, однако, среднее значение просветности для большого набора параллельных сечений какого-либо фиксированного образца равно пористости этого образца. Это свойство позволяет приближенно считать пористость и просветленность практически равными величинами для реальных пористых сред со случайной структурой: n ® m. Процедура осреднения. Как правило, внутренняя поверхность порового пространства имеет случайную структуру, поэтому прямое описание движения жидкости, а также теплопереноса, массопереноса и т. д. во всех подробностях оказывается невозможным или возможным в небольшом числе частных случаев (например, для искусственно созданной периодической среды). К счастью, однако, в большинстве приложений характерные линейные размеры L фильтрационных задач значительно больше характерного размера пор d , а при практическом изучении фильтрационных явлений обычно интересуются осредненными характеристиками процессов, происходящих в процессе фильтрации. Это позволяет при описании крупномасштабных явлений рассматривать пористый материал как сплошную среду, характеристики которой (плотность, давление, температура и т. д.) в каждой точке получаются в результате осреднения по некоторой окрестности радиусом l , содержащей достаточно большое число пор. При осреднении исходят из необходимости придерживаться соотношения d ^ l ^ L .
Окрестность каждой конкретной точки порового пространства радиусом
l
называют репрезентативным элементарным объемом (REV, representative elementary volume). Это может быть любая окрестность (куб, эллипсоид, шар) с характерным линейным размером
l
. Далее в качестве такой окрестности используется шар радиусом
l
. При этом величина
l
должна выбираться так, чтобы результаты осреднения мало зависели от объема
VB
.
Если необходимо осреднить некоторую физическую величину
A
(
x
,
t
),
x
=
(
x
,
y
,
z
)
, определенную в жидкости, то, поскольку жидкость отсутствует в пористом скелете, величина
A
(
x
,
t
) доопределяется в этих областях нулевыми значениями. Среднее значение
A
(
x
0,
t
) величины
A
(
x
,
t
) в точке
x
0 определяется в REV с центром шара в точке
x
0 радиусом
l
(обозначим это множество
B
i
(
x
0
)
)
(A
(
x
0
,
t
)} =
V-
J
A
(
x
,
t
)
d
v
.
B B
l
(
x
0
)
Здесь
V
B
— объем шара
B
l
(
x
0
)
, в котором присутствуют и элементы скелета.
Так, полученное среднее значение
A
(
x
,
t
)
в каждой точке
x
(индекс 0 у вектора
x
опущен для удобства) порового пространства является непрерывной и почти всюду дифференцируемой функцией координат центра объема
x
и времени
t
. Причем величина
A
(
x
,
t
) будет уже определена везде в рассматриваемой области порового пространства, даже если точка
x
попадает внутрь пористого скелета.
Скорость фильтрации.
Для характеристики массопереноса при движении жидкости через пористую среду вводится векторная величина — скорость фильтрации
u
. Рассмотрим определение
u
на примере движения жидкости вдоль трубки, заполненной пористым материалом. Для такого течения скорость фильтрации определяется как вектор
u
, направленный в сторону движения жидкости, величина которого равна объемному расходу жидкости
Q
(объему жидкости, протекающему в единицу времени) в расчете на единицу площади полного поперечного сечения трубки, включающего как поры, так и пористую среду. Скорость фильтрации, имеющая размерность скорости, тем не менее не равна скорости движения отдельных частиц жидкости. Постоянство объемного расхода однородной несжимаемой жидкости можно записать в виде
Q
=
|u|
S
=
vS
p
, (П3)
где Q — объемный расход жидкости через трубку; v — среднее значение проекции микроскопической (внутренней) скорости частиц v(x, t) на ось трубки, вычисленной по площади сечения, занимаемой порами. Отсюда v = MS = H . H, Sp n m
т. е. средняя скорость частиц жидкости приблизительно в раз больше скорости фильтрации.
m В общем случае неодномерного движения жидкости в пористой среде скорость фильтрации определяется как вектор u , проекция которого на некоторое направление равна объемному расходу жидкости через единичную площадку, перпендикулярную данному направлению. С помощью этого определения легко вычисляется объемный расход Q и массовый расход QM жидкости через произвольную поверхность S, проведенную внутри пористой среды
Q
=
j
u
•
n
d
s
,
Q
m
=
J
p
u
•
n
d
s
.
S S
Здесь
n
— единичный вектор внешней нормали к поверхности
S
;
p
— плотность фильтруемой жидкости.
Удобство использования скорости фильтрации состоит в том, что с ее помощью можно находить расход жидкости без использования информации о пористости, которая явно не входит в последние поверхностные интегралы.
Скорость фильтрации
u
, равная
u
=
m
V
, трактуется как вектор средней скорости жидкости по объему
VB
(т. е. по совокупному объему порового пространства и скелета). Здесь
V
— вектор средней внутренней скорости, определенной осреднением текущей (микроскопической) скорости жидкости
v
=
v
(
x
,
y
,
z
,
t
)
только во внутрипоровой области объема
VB
, что полностью соответствует процедуре осреднения, описанной выше.
Работа выполнена в ИАП РАН в рамках НИР по государственному заказу ФАНО 0074-2014-0010, государственный регистрационный номер: АААА-А16-116041310008-3.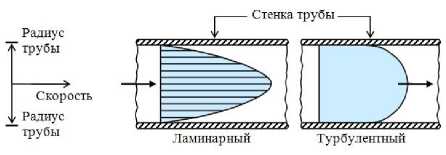
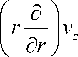
Список литературы Об одном новом методе электроакустического преобразования. Теория, основанная на электрокинетических явлениях. Ч. I. Гидродинамический аспект
- Shishov S. V., Andrianov S.A., Dmitriev S.P., Ruchkin D. V. Method of converting electric signal sinto acoustics oscillations and an electric gas-kinetic transducer. US Patent no. US 8,085,957,B2 Dec. 27, 2011.
- Духин С.С., Дерягин Б.В. Электрофорез. М.: Наука, 1976. 332 с.
- Ньюмен Дж. Электрохимические системы. М.: Мир, 1977. 464 с.
- Bruus H. Theoretical microfluidics. Oxford University Press, 2008. 346 p.
- Князьков Н.Н., Шарфарец Б.П., Шарфарец Е.Б. Базовые выражения, используемые в электрокинетических явлениях. Обзор//Научное приборостроение. 2014. Т. 24, № 4. С. 13-21. URL: http://213.170.69.26/mag/2014/abst4.php#abst2.
- Физическая энциклопедия. Т. 5. М.: БРЭ, 1998. 760 с.
- Щукин Е.Д., Перцов А.В., Амелина Е.А. Коллоидная химия. М.: Высшая школа, 2004. 445 с.
- Ландау Л.Д., Лифшиц Е.М. Теоретическая физика. Т. 6. Гидродинамика. М.: Наука, 1988. 736 с.
- Биркгоф Г. Гидродинамика. Методы. Факты. Подобие. М.: Иностр. лит-ра, 1963. 244 с.
- Шарфарец Б.П., Курочкин В.Е. К вопросу о подвижности частиц и молекул в пористых средах//Научное приборостроение. 2015. Т. 25, № 4. С. 43-55. URL: http://213.170.69.26/mag/2015/abst4.php#abst6


