Об одном новом методе электроакустического преобразования. Теория, основанная на электрокинетических явлениях. Ч. II. Акустический аспект

В патенте [1] был предложен новый метод генерации акустических волн. Настоящая работа является продолжением работы [2], в которой было начато альтернативное физическое обоснование предложенного в [1] изобретения в части его гидродинамического аспекта. Здесь рассмотрим акустический аспект описанного в [1] изобретения.

В работе [2] приведена система уравнений На-вье—Стокса [2, (3а), (6), (7)], позволяющая описать гидродинамику стационарных электроосмотических процессов в капилляре. При этом само уравнение [2, (6)], полученное из уравнения На-вье—Стокса для несжимаемой жидкости, описывает течение стационарной вязкой несжимаемой жидкости при условии баланса сил трения и электрических сил. Краевое условие [2, (7)] говорит о равенстве нулю тангенциальной составляющей скорости жидкости на границе скольжения v_t = 0. Кроме того, в общем случае должна быть равна нулю нормальная составляющая скорости жидкости на границе скольжения v_n = 0 [3, с. 36]. Наконец, возникает еще одно краевое условие для нормальной производной потенциала ϕ стороннего электрического поля E : на поверхностях сколь-

∂ϕ жения должно выполняться условие = 0 [3, ∂n

• с. 37].

УСЛОВИЯ, ПРИ КОТОРЫХ СРЕДУ МОЖНО СЧИТАТЬ НЕСЖИМАЕМОЙ

Остановимся на критериях, когда среду можно считать несжимаемой. Свойство сжимаемости среды характеризуется величиной Δ ρ / ρ относительного изменения плотности среды ρ в гидродинамическом процессе. Величина А р / р ^ 1 при выполнении следующих условий [4, с. 253]:

• 1)    | v| « c ;     2) L « t* • c ;

• 3)    gL <<  c ²; 4) в •A T << 1.

Здесь v , c , L , t* и ΔT — соответственно харак- терные для рассматриваемого процесса скорость среды, скорость звука, длина, время и изменение 1 ∂ρ температуры; β =     — коэффициент теплово-

ρ ∂T го расширения; g — ускорение силы тяжести. В случае незначительного влияния изменения температуры AT на параметры среды, а также возможности пренебрежения силой тяжести существенными условиями несжимаемости среды остаются условия 1), 2). Однако при изучении явлений, само существование которых обусловлено способностью среды изменять плотность (распространение звука, конвекция и т. д.), нельзя пренебрегать величиной Ар / р , как бы мала она ни была.

ГИДРОДИНАМИЧЕСКИЕ УРАВНЕНИЯ

С учетом того, что в акустических процессах жидкость нельзя считать несжимаемой, закон сохранения импульса запишем применительно к движению вязкой сжимаемой однородной жидкости (без учета силы тяжести) [5, с. 73]

• -v.

р + ( -V ) =

'V t   ^V ’

( n A

= ^-V p . + n ^{A v} . + 1 q + 3 |VV- v . + P el E. .     (1)

Здесь η, ς — по-прежнему динамическая и объемная вязкости соответственно; p. — давление; v. — вектор скорости в среде; р. — плотность среды; ρel — объемная плотность заряда в двойном электрическом слое (ДЭС); E. = E0 + E, где постоянное электрическое поле E0 = const модулируется коллинеарным ему электрическим, зависящим от времени вектором E (E х E0 = 0); величины, помеченные индексом ., обозначают поля, возбужденные полем E.. Пометим поля, вызванные электрическим полем E0 , нижним индексом 0: p0 , v0 . Кроме того, обозначим через ρ0 невозмущенное значение плотности, имеющее место в том числе и при воздействии только поля E0 , поскольку при стационарном электроосмосе среда считается несжимаемой. Тогда, если принять во внимание допущение о том, что скорости процессов соответствуют малым значениям числа Рейнольдса Re ^ 1,1) то в (1) можно пренебречь конвективным членом р.(v.-V) v. [5, с. 89], что превращает нелинейное уравнение (1) в его линеаризованную версию р —. = -Vp^ + nAv^ +1 q + — 1VV - v + реХE . (2) .                 .          .                          . ei .

д t                   V 3 у

Поскольку в линейном случае справедлив принцип суперпозиции, то можно записать, что р . = р о ⁺ р , Р . = Р о ⁺ Р , ^v . = V o + V .

Пусть стационарный электроосмос подчиняется усеченному уравнению Навье—Стокса (1) (см. [2])

— A V o + р_е , E o = 0,                   (3)

(что означает баланс сил трения и постоянных электрических сил), т. е. постоянная разность давления отсутствует V p ₀ = 0, член с временной производной равен нулю из-за стационарности процесса, член, содержащий дивергенцию (    —

I ^ + — IVV - v0, равен нулю вследствие соглаше ния о несжимаемости стационарного процесса. Или формально

V p о = 0;         = 0;        V- V o = 0.       (4)

о t

Система (3), (4) описывает стационарное электроосмотическое течение под воздействием постоянного электрического поля при рассмотрении баланса электрических сил и сил трения.

На долю возмущенного решения приходится остающаяся часть уравнения

• р .-- = -Vp + —Av + I q + n |VV-v + PelE .(5)

• - 1V

Для придания уравнению (5) линейного акустиче-

_ _ _      -                    _ _   _d ского вида необходимо линеаризовать член ρ

. д t до акустических величин первого порядка, а именно

• - v   _         (

ро — = -Vp + —Av + I ^ +T-|VV-- + ре1E .   (6)

• - 1                 V

Часто для быстроразвивающихся процессов принимается предположение о справедливости соотношения Стокса [6, с. 385], сводящееся к равенству нулю объемной вязкости q = 0 .

В этом случае уравнение (6) упрощается ро I- = -Vp + —Av + —VV" - + PelE ,        (6а)

• - 1                 3

позволяя обходиться только значением динамической вязкости η . Впрочем, о правомерности применения соотношения Стокса см. рассуждения в работе [7, с. 208, 209].

К уравнению движения (6) либо (6а) необходимо добавить линеаризованное уравнение непрерывности

' р + Р о ^ v = 0, д t

а для замыкания системы четырех уравнений для пяти неизвестных добавить уравнение состояния. Для простоты принимаем среду баротропной, что означает однозначную зависимость между давлением в среде и ее плотностью.²⁾ Для давления p и соответствующей ей плотности ρ это означает

p l = f ( P l ) , или в линеаризованном виде

5 p l

S P l

р l = р о

P = с 2 P,

Подстановка (9) в уравнение (6) с учетом известного равенства из векторного анализа VV - F = V x V x F + A F , где F — некоторый вектор, дает³⁾

дv, „ f     4 Y

P0    + VP-I S + П |Avl - PelE д t V    3 J

+

Po ^7 - nAv t

= 0.

+

Здесь в первой квадратной скобке стоят потенциальные, а во второй квадратной скобке — соленоидальные вектора. Напомним, что E = -V ф — потенциальный вектор, где ϕ — скалярный потенциал электрического поля E . Применяя к (10) стандартную процедуру разделения потенциальных и соленоидальных составляющих, описанную, например, в работе [10, с. 54], получаем уравнение для потенциального течения

где с — скорость звука в среде. Из (8) имеем

дp _ 2 др "dt ~ "dt "

(8а)

Система (6)–(8) представляет собой замкнутую систему линейных уравнений акустики для однородной, вязкой, баротропной среды (см., например, [8, § 1]), где v — вектор колебательной скорости, p — акустическое давление, ρ ₀ — равновесное значение плотности, а ρ — возмущение плотности, вызванное возмущением давления, т. е. акустическим давлением p .

РЕШЕНИЕ УРАВНЕНИЙ (6)–(8)

Способ решения

Удобный способ решения системы (6)–(8) состоит в том, что на основании известной теоремы Гельмгольца векторного анализа принимается стандартное представление вектора скорости v в виде суммы потенциальной v _l и соленоидальной v _t частей (см., например, [9, с. 345])

• v = v l + v _t , v l = 7Ф , v _t = Vx T , V- T = 0. (9)

Здесь Ф и T — соответственно скалярный и векторный потенциалы поля скоростей v . При этом вектора v _l и v _t удовлетворяют уравнениям

Vx v l = 0,              V- v _t = 0.

dv,        f    4 Y„

Po — = -VP + | S + "TP lAvl + д t            V

и соленоидального течения

Po    = nAvt.

д t

Подставляя в (11), (12) значения для vl и vt из (9), преобразуем их к виду дVФ  „ f

Po—— = -Vp + | S + -П |AVФ-PelVф, д tV или дФ       f

Po — = -P + | S + TP 1АФ-PelФ д t          V для скалярного потенциала и дТ

P o — = П ^{А Т} д t

для векторного потенциала.

Учитывая соотношение (8) между акустическим давлением p и акустическим возмущением плотности ρ, трансформируем (13) к виду дФ 2 f 4 Y

P o — = ^- 2 P + I S ⁺ - П | ^АФ- P el Ф .       ⁽¹⁵⁾

д t             V 3 J

Пусть вектора E ₀ и E направлены вдоль оси Oz ( E ₀ = ( 0,0, E 0 ) , E = ( 0,0, E ) ) и вектор E , вызывающий акустические колебания, имее т гармоническую зависимость от времени E = Ee ®t , где E = const — амплитуда колебаний. Тогда потенциал ϕ вектора E в этом случае определяется из соотношения

Vф = ^ = -Ee-®.

5 z

Интегрируя последнее равенство, имеем

Ф = - Eze - ®t + ф ( 0 ) e - ®t ,            (16)

где ф ( 0 ) = ф ( z )| _ . В дальнейшем полагаем ф ( 0 ) = 0.

Преобразуем уравнение (13). Для этого воспользуемся условием непрерывности (7) и соотношением (8) между величинами избыточной плотности ρ и акустического давления p :

2   „         5Р            п p = ср. Получаем — = - р c V • v. Подстановка 5t       0

в последнюю формулу выражений (9) дает

I p = ^- Р о ^c '^V • ^v = ^- Р о ^{c 2V} • ^v i = ^- P o ^{c 2АФ .} a t

Случай гармонического стационарного процесса

В гармоническом случае сохраняем для полей те же обозначения для амплитуд, подразумевая наличие гармонического множителя e ^{- i m t} . Из последнего уравнения имеем для амплитуд

-i® p = - p0 c2 АФ, или окончательно p = Bec- АФ.              (17)

i ω

ОБЪЕМНАЯ ПЛОТНОСТЬ ЗАРЯДА

Остановимся на величине ρ _el — объемной плотности заряда, соответствующей распределению зарядов в диффузионном слое электроосмотического процесса при различных поверхностях раздела фаз. Наиболее легко вычисляется распределение ρ _el в случае т. н. приближения Дебая. Так, для плоской границы раздела фаз (плоскость x = 0) величина p el на расстоянии x от плоскости раздела вычисляется по формуле [11, с. 148], [12]

P ei ( ^x ) = - ее о ^А Ф = - ее о

^ее o Q λ D ²

С

exp

V

С учетом (17) выражение (13) для гармонического сигнала примет вид

p c      I

-i®PoФ =—0— АФ + I q + -п|АФ- Ре1ф.

i®        V

С учетом (16) выражение (18) переписывается так:

- i ®р ₀ Ф = - -^{P o} c-iω

I 4 I

АФ +1 ^ + jn |АФ + pel Ez.

д ² ф d x²

λ D

а для круговой цилиндрической поверхности раздела фаз — по формуле [11, с. 149], [12]

Pel ( r ) =

ее o Q I о ( r / ^ d ) ^ D I о ( a / X d ) .

Здесь I ₀ — модифицированная функция Бесселя нулевого порядка; z — текущее расстояние от плоскости скольжения в случае плоской границы; r — текущее значение радиуса капилляра радиусом a (здесь под a понимается радиус до поверхности скольжения капилляра); λ_D — длина Дебая. q -потенциал [2] здесь обозначен через q во избежание путаницы с устоявшимся обозначением для объемной вязкости ς . Все остальные обозначения соответствуют обозначениям, принятым в работе [2].

В случае плоской границы раздела уравнение (19) с учетом (20) запишется так:

B c      I     4

-i®p0Ф = —0— АФ + I q + —n 1АФ-i®       V    3 J

или в каноническом виде

ω

А + c?

V

q

⁰₂ exp λ_D

—

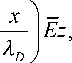
I .4 i ®| q + — n

V 3

ρ ₀ c ²

Ф =

—

ito ££ ₀C ρ ₀ c λ_D

(   . (   4 W 1

itoI c + -n I

1к_____3

P o c ²

г

exp

—

к

X IF Ez .

А 7

к

Введем обозначение для

волнового числа по-

тенциальных волн (см., например, [13, 14])

ω k =—

c

1—

■ (    4 11

i to c + — n

к 3 1

— 1/2

ρ ₀ c ²

Тогда последнее выражение запишется в виде

2    r    <

[A + k ² ]Ф = _2 £ exp — I Ez .        (22)

^toP 0 ^ D     к ^ D 7

же плохих проводниках, время релаксации заряда τ достаточно мало. Так, в морской воде время релаксации порядка т = 2 - 10 ^{— 10} с; даже в таком плохом проводнике, как дистиллированная вода, оно не более 10 ^{— 6} с". Эти величины соответствуют частотам от 1 МГц до 10 ГГц, что явно далеко выходит за границы акустического диапазона.

Формально задача считается решенной, если определены скалярный Ф и векторный Т потенциалы. Вектор колебательной скорости v определяется после этого из (9). Поле акустического возмущения плотности может далее быть определено из выражения (8). Скалярный потенциал определяется выражением (19), векторный — выражением (14). Поле давления определяется из (17), однако может быть определено иначе с помощью выражений (17) и (22) или (23) в виде

В случае круговой симметрии задачи (ось цилиндра совпадает с осью Oz ) лапласиан равен

.   1 д ( 97 d2

A =--I r — I +--- и уравнение (19) с учетом

r 9 r к dr 7 9z

(21) преобразуется к виду

Р =

ρ ₀ c ² i ω

(

k 2Ф +

ikL ^^ Ez exp ωρ ₀ λ_D

f

к

x λ D

\

1 9 ( 9 I   92

-—I r— I + —2 r 9 r к dr 7 9z2

+ k2 >Ф =

для плоской границы раздела фаз и

Р =— р ° £- [ k =Ф+J k L fe^ Ezl^lbl'

^{i to} к        ^top 0 ^ D      I 0 ⁽ a ¹ ^ D ) 7

для цилиндрической границы раздела фаз.

i k ² ее o C I o ( ^{r 1} ^ d ) E_z ^toP o ^ D I 0 ( a I ^ D ) '

Таким образом, для амплитуды скалярного потенциала скорости Ф получены неоднородные уравнения Гельмгольца (22), (23). Правая часть этих уравнений, как и в случае стационарного электроосмоса ([2, выражение (9)]), пропорци о нальна амплитуде электрического потенциала E и величине дзета-потенциала C , а также обратно пропорциональна величинам динамической вязкости n и объемной вязкости c • Кроме того, Ф , как и в стационарном случае, пропорциональна произведению диэлектрической проницаемости среды и электрической постоянной εε ₀ .

Замечание . Как отмечалось в [2], в моделях электроосмотических процессов принимается допущение, что распределение заряда ρ _el в ДЭС является стационарным и не зависит от приложения стороннего стационарного электрического поля, в данном случае E ₀ . В случае добавления переменного поля E , даже если предположить, что оно влияет на структуру ДЭС, возможное влияние его на структуру ДЭС на акустических частотах можно не учитывать, т. к. [15, с. 27]: "Во всех, да-

ВЛИЯНИЕ ВЕКТОРНОГО ПОТЕНЦИАЛА

Уравнение (14) для векторного потенциала в гармоническом случае записывается так:

A T + i ^{toP 0}- Т = 0,            (26)

η или в виде уравнения Гельмгольца

A T + k ²T = 0 .

Здесь k t = ( 1 + i ) 1 5 , где 5 = 12 ^П— = V 2v I to , где ρ 0 ω

ν — кинематическая вязкость, а величина δ называется глубиной проникновения вязких волн (см., например, [13, 14], [16, с. 63]). Решение уравнений типа (26) разобрано, например, в [16, § 19]. Его решение для плоской волны представляет собой неоднородную плоскую волну с экспо- x ненциально убывающей амплитудой e δ , где x — длина пути прохождения плоской волны от плоскости x = 0 .

Глубина проникновения вязкой волны δ для воздуха при температуре 20 °C равна 5 = = V 2 - 1.51 - 10 ^{— 5}1 to .

Глубина проникновения вязкой волны в воздухе и воде на разных звуковых частотах

Частота, Гц	Воздух		Вода
	δ , м	x 0.1 , м	δ , м	x 0.1 , м
20	5 - 10 - 4	1.1 - 10 - 3	3 - 10 - 4	3 - 10 - 4
100	2.2 - 10 - 4	5 - 10 - 4	5.7 - 10 - 5	1.3 - 10 - 4
1000	7 - 10 - 5	1.6 - 10 - 4	1.8 - 10 - 5	4.2 - 10 - 5

Глубина проникновения вязкой волны δ для воды при температуре 20 °С равна 5 = = 4 2 - 1.06 - 10 ^{- 6} / ω . В таблице представлены величины δ для воздуха и воды на частотах 20, 100 и 1000 Гц, а также соответствующие значения величины x _0.1 , при которой экспоненциальный мно- _ x 0.1

житель e ⁵ = 1/10 (т. е. амплитуда волны падает на порядок).

Как видно из приведенных формул и из таблицы, глубина проникновения вязкой волны δ в воздухе больше, чем в воде, и обратно пропорциональна корню квадратному из частоты. Характер изменения величины x _0.1 примерно повторяет поведение величины δ .

Поведение величин δ и x _0.1 следует учитывать при расчетах полевых характеристик акустического поля через скалярный и векторный потенциалы. В случае, если x ₀₁ « a , можно ограничиваться при расчетах учетом только скалярного потенциала. В противном случае необходимо учитывать оба потенциала.

ОТЛИЧИЕ АКУСТИЧЕСКОГО ЭЛЕКТРООСМОСА ОТ КЛАССИЧЕСКОГО

Уравнения

Классический электроосмос в отличие от акустического предполагает временнýю стационарность, несжимаемость жидкости и присутствие сторонней силы только в виде постоянного электрического поля. Отсюда — использование простой математической модели в виде упрощенного уравнения Навье—Стокса, решением которого является стационарное течение v с единственной составляющей v_z , совпадающей по направлению с действием внешнего вектора электрической напряженности Е ₀ = ( 0,0, Е ₀ z ) . Решение этого уравнения тривиально [3, с. 34], [17, с. 218] и не нуж-

дается в использовании векторного потенциала Ψ .

В акустическом электроосмосе уравнение На-вье—Стокса много сложнее. Во-первых, оно нестационарно в смысле зависимости от времени, во-вторых, жидкость уже нельзя считать несжимаемой и, в третьих, нельзя обойтись простым балансом сил между электрическим полем и силами трения, необходимо учитывать также и силу акустического давления. Ниже рассматриваются следствия этого усложнения.

Принимаем для простоты, что задача расчета полевых характеристик в акустическом электроосмосе описывается потенциалом Ф , а потенциалом Ψ можно пренебречь. Тогда, как видно из (22)-(26), поля Ф , v и p для плоской границы раздела фаз зависят от переменных x и z , а для цилиндрической поверхности раздела фаз — от переменных r и z .

Согласно (6), наличие зависимости акустического давления p от двух координат (p = p ( x , z ) для плоской границы либо p = p ( r , z ) для цилиндрической границы) приводит к появлению, кроме v_z , еще одной составляющей скорости — соответ-

ственно v_x или v_r , что отличает от случая класси-

ческого электроосмоса, где существует только одна составляющая вектора скорости v_z .

В случае, когда

границы или

д ф

д z

дф дp -- ~ -- дz   дz

»

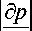
д x

для плоской

~

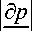
д z

»

д p д r

для цилиндриче-

ской, можно считать, что присутствует одна составляющая течения v_z . Здесь ϕ — потенциал

вектора электрической напряженности E = -V ф .

Краевые условия

В классическом электроосмосе ставятся следующие краевые условия [3, с. 34], [17, с. 218]:

• 1)    вектор скорости v на плоскости скольжения равен нулю; для плоской границы раздела это означает v| x = a = 0, или, учитывая что v = ( 0,0, v z ) : v z l x = a = 0; Для цилиндрической границы раздела соответственно v| = 0, или v I = 0;

r = a                   z\r = a

• 2)    вне диффузного слоя производные электро-

• „ дv7   „ дv7

осмотических скоростей —- = 0 и —- = 0 соот-дx        дr ветственно для плоской и цилиндрической границ;

• 3)    вне диффузного слоя потенциал Ф _eo двойного электрического слоя стабилизируется и становится равным нулю, что отражается равенства-

• дФ   п дФ

ми —— = 0 и —— = 0 соответственно для пло-дx         д r ской и цилиндрической границ раздела; кроме того, вне диффузного слоя Фео = 0.

Очевидно, что в случае акустического электроосмоса при наличии второй составляющей вектора скорости, кроме условий 1–3, ко второму краевому условию для классического электроосмоса необходимо добавить условие равенства нулю второй составляющей скорости на поверхности скольжения: v I = 0 и v I = 0 соответственно. Учиты- x l x = 0                 rir = 0

вая краевое условие 1), последние краевые условия и то, что составляющие вектора скорости v нулевые — v y = 0 и v ^ = 0 для плоского и цилиндрического случаев соответственно, можно в общем виде записать краевое условие для акустического электроосмоса

7Ф| = 0,

a

• т. е. равенство нулю градиента скалярного потенциала на поверхности скольжения.

ВЫВОДЫ

В работе предложены необходимые уравнения и краевые условия для описания акустических полей, вызываемых электрокинетическими явлениями: наличием двойного электрического слоя и приложенного электрического поля, являющегося суммой постоянного поля и электрического поля, несущего акустическую информацию. Уравнения рассматриваются для условий вязкой несжимаемой и сжимаемой жидкости для условий расчета соответственно гидродинамики стационарного электроосмотического процесса и зависящего от времени акустического процесса. Как видно из полученных выражений, процессы, происходящие при акустическом электроосмосе, имеют как много общего, так и содержат некоторые отличия от процессов классического электроосмоса. Разработанная в работе физическая модель и полученные соответствующие математические выражения позволяют рассчитывать акустические характеристики излучателя, основанного на наличии элек-трокинетических явлений, и оптимизировать его устройство.

Работа выполнена в ИАП РАН в рамках НИР по государственному заказу ФАНО 0074-2014-0010, государственный регистрационный номер: АААА-А16-116041310008-3.