Об одном парадоксе закона больших чисел для максимальных серий в последовательной выборке

1 . Серии в последовательной выборке, представляющие собой группы подряд стоящих индивидуальных значений, расположенных по одну сторону от медианы (знаковые серии) или образующих монотонную последовательность (трендовые серии), как было показано в [1, 2], имеют отчетливую спектральную структуру с устойчивой воспроизводимостью. В [1] был получен точный закон распределения длины максимальной серии обоих типов. В [2] установлен закон распределения числа серий фиксированной длины и получены его нормальные (для коротких серий l <  7 ) и Пуассоновские (для l >  7 ) асимптотики при большой длине последовательности. Пос-

ледние из указанных результатов легко позволяют установить предельную форму закона распределения максимальной длины серий. При этом, как оказывается, предельная форма распределения максимальной трендовой серии обладает довольно неожиданным свойством, которое без преувеличения можно назвать “парадоксом вырождения”. Этот парадокс заключается в том, что при

Затем вторая мода поглощает первую (распределение опять вырождается), и это процесс закономерно циклически повторяется. При умеренно больших n ( ~ 10 3 ) этот эффект проявляет себя, как показано в [1], в виде апериодических колебаний дисперсии и моментов более высокого порядка.

Серии первого типа (знаковые) ведут себя не столь парадоксально. Их предельная форма рассеяния подобно выборочному размаху [3] является стационарной и смещается вправо по оси n со скоростью log ₂ n .

2 . Асимптотику распределения длины максимальной серии L_n найдем, используя полученные в [2] Пуассоновские оценки для числа ~ нере-куррентных серий фиксированной длины R_l ( n ) . Для знаковой серии длины l , расположенной выше медианы в последовательности длиной n эта оценка, согласно [2], составляет:

неограниченном возрастании длины последовательности n длина максимальной трендовой серии перестает быть случайной, т.е вырождается в

фиксированное значение: P { L_n 1 = l 1 ( n 1 ) } « 1 .

Причем, с дальнейшим возрастанием n эта

изолированная мода расщепляется на две, и вторая мода l 2 = l 1 + 1 , постепенно возрастая, сравнивается с первой:

P R+ (n) = k }= exp^ k j.

Используя двойственность величин R l ⁺ ( n ) и L + , ряд распределения последней можно записать в виде:

p+= P {L■=l }=

= P { R * ( n ) > o } p { R „ + ( n ) = 0, V m >  l } . ⁽¹⁾

Подставив в (1) Пуассоновские вероятности, получим:

PL = L ( n ) } « P { l = L ( n ) + 1 } « ¹ n ₂      1 2              n ₂      1 2              2

pL

1 - exp

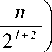
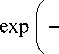
to

z m = l + 1

n m + 2

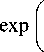
1 - exp

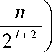
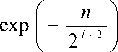
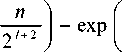
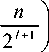
, 1 <  l <  n .

Асимптотический ряд (2) очевидно сходит-

ся к 1 как У p l = exp( - -^- ^- exp( - n ) .

I =1                ^{2               4}

Для величины L_n = max { L 1 , L_n } , собствен но и являющейся максимальной длиной знако

-

-

вой серии, определённой согласно [1], ряд распределения найдём по формуле максимума двух

независимых величин с одинаковым законом

распределения:

P i = ² P i y P ^{1 1} P l 2 .        (3)

k <  l

Подставляя в (3) члены ряда (2) и пренебрегая слагаемыми ~ e - an , получим

P i » ^exP^{( -} 2 n T ) ^{- ex}P^{( -} у ) .      (4)

Для рядов (2), (4) очевидно тождество Pi _{+ 1} = P l или, что фактически то же самое, P l ^{( n} ) = P i ^{(2 n} ) .

Таким образом, ряд (4) сдвинут на 1 вправо по оси l относительно ряда (2).

Переходя в (4) к величине t = i - log2 n              (5)

получаем независящую от n предельную форму (4):

f ⁽ t ) = ^exP^{( -} ^У) ^{- ex}P^{( -} 2? ) ’ ^- ” <  t <  ^да , (6)

вид которой с последующим квантованием показан на рис.1. Числовые характеристики (6) равны:

да                        i да Л 1

^p = J t^{f (} t ) dt =^ J ^ e ²

e

- x

ln( x ) — = x

C 1 1 ^™^™      1

ln(2) 2

« 0.3327

, (7)

да1

^ ² = J t ² f ( t ) dt -p ² 1 — =

да

C ₂ C 1     1

ln ² (2)   ln(2)   3

^^^^^^^.

, (8) p ²1 — « 3.5904

C k

где C_k , k = 1,2 - Эйлеровы интегралы [3,4]:

да                              1

= ( - 1) ^k J e x ln ^k ( x ) dx ; ~ в (8) — поправка о

на группировку (6). Таким образом, среднее значение длины максимальной знаковой серии составит

P n « 3 + ^log 2 ⁿ ,

дисперсия определяется согласно (8), а предельная форма рассеяния имеет вид (6).

3 . По аналогичной схеме, используя Пуассоновские оценки для трендовых серий [2]:

( ~

R_i ( n ) = k } = exp( - k ( n - 1)

получаем:

1 ² 1 1 - L ( 1 1 2)! )

p { L_n = I } = p l = [1 - exp( - ( n - 1) ¹ +^{1 1} )] x

^{1 n 1}                                (i 1 2)!

m ² + m ^{- 1}

x exp[-(n -1) у         ] = m=i 11 (m 12)!

1 1 1                     I (10)

= ^exp^{( - (} n ^- 1)      ) ^{- ex}p^{( - (} n ^- 1)      ),

( i 1 2)!                  ( i 1 1)!

2 <  i <  n .

Сумма ряда (10) составит:

n

У i=2

n ² - 1            n - 1

p i = ^{exp( -}7 П Г 2)!’"^{exp( -} 3 ) ■

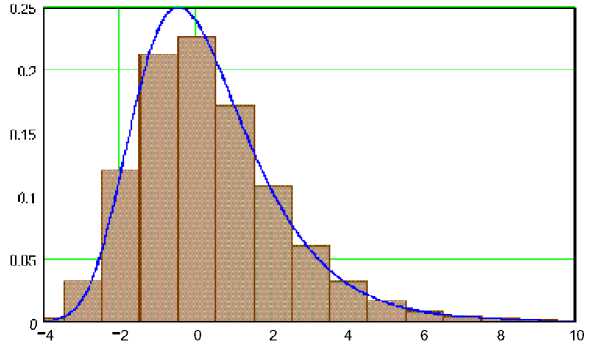
Рис. 1. Предельное распределение длины максимальной “знаковой” серии и его сглаживающая кривая

По аналогии с (3), (4), для L n = max { L + , L n } получаем

P ^{ L n = ^{l }} = P l = ^exp( - 2( n ^— 1) ^{l + 1}-) ^{— (} t + ²⁾.

^— exp^{( -} 2⁽ n ^— 1) ( j -+i).), 2 <  l <  n .

В дальнейшем, поскольку речь идет о больших n , различием между n и n - 1 в (10)-(12) пренебрежем и положим l >  10, 2 n = a l ! , где a - константа ~1.

Для соседних членов ряда (12) с номерами l — 1 и l будет иметь:

ние становится “почти вырожденным”).

Последовательность значений n 1 ( l ) , соответствующих полному вырождению (изолированной моде) будем искать в виде:

2 n 1 ( l ) = l в ( l ) , (16) где в ( l ) определим из условия p_{l — 1} ^ max . Для члена ряда (12) с номером l _— 1 будем иметь:

P l — 1 = ^exP — ^e j + 1) ^{— ex}P⁽" ^{e ( l —} 1)) * ^e "^{Р — e}" ^в .(17)

Подстановкой e—в = и приходим к функции вида и —ul,                 (18)

максимум которой достигается в точке

P i — 1 = ^exP^{( — a} J + 1) ^{— ex}P^{( — a ( l —} 1)) * e

,- ^a

P l = ^exP^{( —}

1 l

) — exp(—a   ) * 1 — e l + 2 l +1

,—a

и =

1 Л 1 11 l J

откуда, после обратной подстановки, находим

Приравняв pl—1 = pl = -^ , получим a = ln2 .

Таким образом, последовательность

ⁿ 2 ^{( l} ) =

l ! • ln2

соответствует наличию симметрично расщепленной двойной изолированной моды:

P{l = l — 1}* P{l = l}* 1

n 2                      n 2            2

(остальные члены ряда (12) в сумме составляют ничтожно малую вероятность, и распределе- в )* JnL * ^ l—1 l ■

Таким образом, значения

(l — 1)!ln l n1(l) [      2      ]

соответствуют фазе существования изолированной моды (полного вырождения закона распределения): P { L_{n 1} = l — 1 } * 1 .

Область значений n 1 ( l ) <  n <  n ₂ ( l ) соответствует периоду “зарождения” и роста второй моды { L n = l } . Затем, на интервале n ₂( l ) <  n <  n 1 ( l + 1) новая мода “поглощает” старую, и процесс циклически повторяется. Эво-

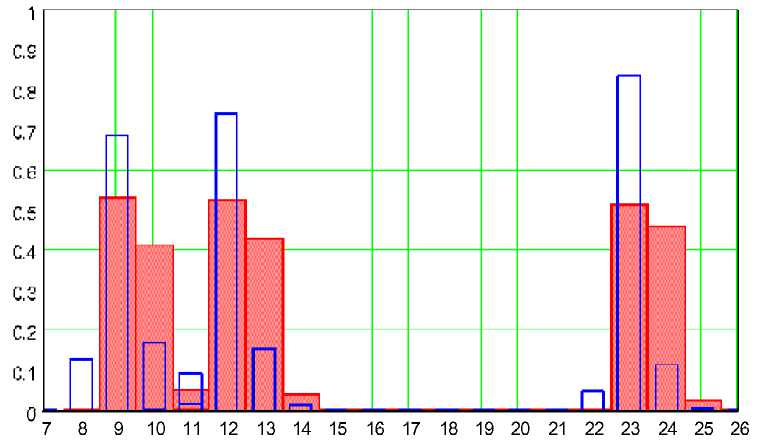
Рис. 2. Эволюция распределения длины максимальной трендовой серии.

Фазы изолированной и симметрично расщепленной моды при n =4.178 х 10 5 ; 1.258 х 10 6 ; 6.143 х 10⁸; 2.158 х 10 9 ; 4.108 х 10²² ; 2.150 х 10²³ (слева направо)

люция ряда (12) в зависимости от n показана на рис. 2. При этом фазы полного вырождения рядов (10), (12) совпадают между собой, и (3) пре

, 2

образуется к виду p l = p l = 1 .

В фазе расщепления моды (12) соотношение

• (3)    примет вид:

P i - 1 = Pm

. P i = ² P l Pm ⁺ P l

При этом в точке симметрии

P l - i ( n ₂) = P l ( n ₂) = 2 мода L + расщепляется в

„ +      1

пропорции P l - 1 = —j=

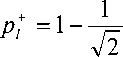
. С воз-

растанием длины последовательности до n + = 2 n ₂ мода L | становится симметричной, а значения L_n перенормируются как

1         3

^P i - 1 = 4, ^P i = 4 .

Таким образом, длина максимальной трендовой серии в большой последовательной выборке становится величиной, закономерно возрастающей с увеличением объема выборки (неслучайной). Тем самым, она не только является надежным критерием случайности выборки, но и, как представляется, сможет послужить ключом к объяснению некоторых, еще не до конца понятых закономерностей в реальных стохастических процессах, в частности, в процессах диффузии и им подобных.