Об одном подходе к идентификации линейных динамических систем

Появление вычислительной техники вызвало широкий интерес к проведению исследований, связанных с разработкой технологий математического моделирования различных объектов, процессов современной науки и техники. Одним из основных этапов, реализующих технологии математического моделирования, являются создание и идентификация математической модели исследуемого объекта. При этом различают идентификацию в широком смысле (структурная идентификация) и в узком смысле (параметрическая идентификация).

В настоящее время предложенная Н. Винером идеология проведения эксперимента с «черным ящиком» (опытного отождествления модели «черного ящика» с объектом-оригиналом) лежит в основе многочисленных разработанных методов идентификации. При этом на начальном этапе эксперимента «черный ящик» представляет собой некоторую систему, о структуре и внутренних свойствах которой ничего неизвестно. Однако внешние факторы, воздействующие на этот объект (входы), и выходы, представляющие собой реакции на входные воздействия, доступны для наблюдений (измерений) в течение некоторого времени. В широком смысле задача идентификации заключается в том, чтобы по наблюдаемым данным о входах и выходах построить математическую модель функционирования рассматриваемой системы. При рассмотрении задачи идентификации в узком смысле предполагают, что известны структура и класс моделей, описывающих реальную систему. В этом случае задача идентификации сводится к определению параметров математической модели (параметрическая идентификация).

В данной статье предлагается подход к параметрической идентификации математических моделей линейных стационарных динамических систем по результатам проведенных измерений фазовых координат системы на некотором промежутке времени.

Постановка задачи

Рассматриваемая в этой статье задача идентификации формулируется следующим образом. Пусть в результате проведения некоторых экспериментов над объектом, замерены его входные (начальное состояние объекта) x0= x0,x0,...,x0 T и выходные (состояние объекта в моменты времени t) переменные x(t) = xx(t),x2(t),...,xn(t) T как функция времени. Требует- ся определить структуру и параметры некоторого оператора, ставящего в соответствие входным переменным x0 выходные переменные x(t) в моменты времени t.

Будем считать, что состояние объекта x(t) (выход) в моменты времени t по начальному состоянию x0 (вход) является решением некоторой задачи Коши x = f(x), x(10) = x0.

В данном случае под структурной идентификацией модели следует понимать определение структуры правых частей f (x) системы. Отметим, что в настоящее время для решения данной задачи в общем случае не существует универсальных методов. В связи с этим при решении практических задач структура правых частей f (x) системы, как правило, зада- ется.

Во многих случаях достаточно адекватным является предположение о линейности. При этом линейные системы позволяют достаточно полно отразить качественные взаимовлияния переменных, характеризующих состояние объекта. Например, при рассмотрении виброза-щитных систем имеет место предположение о малости отклонений фазовых координат от положения равновесия, что позволяет ограничиваться линейными моделями [1 3].

Будем считать, что состояние x(t) = x(t),x2(t),...,xn(t) T некоторого объекта (процес- са) описывается стационарной системой линейных дифференциальных уравнений x = Ax,   x (0) = x0,                                  (1)

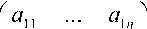
l a i ... a

V n 1     ... nn /

где x ⁰

0   0       0

x 1 , x 2 ,..., xn

начальное состояние объекта; A

n -мерная квад-

ратная матрица размера.

Задача параметрической идентификации сводится к отысканию матрицы A , которая обеспечивает в некотором смысле близость решений задачи (1) и экспериментальных дан- ных.

Пусть в результате проведенного эксперимента при начальном состоянии объекта x ⁰, определены в моменты времени t_x ,..., t_k значения фазового вектора x ( t ), определяющего состояние объекта. Можно считать, что в результате эксперимента задана таблично n -мерная вектор-функция x ( t ) (табл. 1) с компонентами x ( t ), x ₂( t ),..., x_n ( t ) T на промежутке t ₀, t_k .

При этом будем полагать, что количество измерений не меньше, чем размерность фазового вектора kn .

Предположим, что данный набор функций xx(t), x2(t),..., xn(t) , заданный таблично, яв ляется решением системы линейных однородных дифференциальных уравнений (1).

Таблица 1

t	t 0	t 1	…	tk
x 1( t )	x 0	x 1	…	x k
x 2( t )	x 0	x 1		xk
x n ( t )	x"	x n		x nk

Таким образом, поставим задачу поиска матрицы A системы (1) потаблично заданным значениям функций x ( t ), x ₂( t ),..., x_n ( t ) в точках t ₀, t_x ,..., t_k , являющихся решением задачи Коши (1).

Интерполирование решений задачи Коши

Известно [4], что существует единственный полином степени не выше n , принимающий в точках t ₀, t ],..., t_n те же значения, что и интерполируемая функция. Коэффициенты такого полинома могут быть определены из решения некоторой системы линейных алгебраических уравнений.

Таким образом, для каждой из функций x_Y(t ), x₂(t ),..., x_n(t) соответственно строятся интерполяционные полиномы P 1 ( t ), p ²( t ),..., p n ( t ) , коэффициенты которых находятся из решения соответствующих систем линейных алгебраических уравнений. Коэффициенты a j , a / ,..., a j полинома

P^ ( t ) = a j + a j t + a j t ² + ... + a / t n ,   ( /' = 1,2,..., n )

являются решением системы линейных алгебраических уравнений: a^ + a^ty + a^t^ +... + a^t^ = x., a^ + a^t^ + a^tx +... + a^t^ — x.

,

^a 0     ^a i t n    ^a 2 t n "*"..."*" ^a n t n ^{— x}j .

Вычислив производные полинома (2) до порядка n включительно p ¹ ( t ) = a , +2 a₂t + ... + na_ntⁿ 1 , p ^1!( t ) = 2 a ₂ + 2-3 a₃t + ... + ( n -1) na_nt"~ ²,

P⁽ i ) ( t ) = i ! a₍ +... + ( n-i + 1)...( n -1) na_ntⁿ i ,

[ p")(t ) = n! a,, можем найти производные интерполяционных полиномов (2) до порядка n вычисленные в точке tt. Найденные значения производных интерполяционных полиномов (2) в качестве приближенных значений, производных от решений задачи Коши, будем использовать при идентификации системы.

Отметим, что для повышения точности могут быть использованы и другие интерполяционные представления [4]. В данной работе проводится интерполирование полиномом Лагранжа, который наиболее прост.

Идентификации системы

Решение задачи (1), согласно формуле Коши, можно записать в виде x(t) = F(t, t0)x0, где фундаментальная матрица F(t,т) представима в виде матричной экспоненты F(t,т) = eA(t”'*, которая в свою очередь представима в виде матричного ряда [5]

F ( t ,tV F A ^(r) = E + A(t- r) + ^ A ²( t- t)² +•••  -! A k (t- *) ^k +-.. .

Таким образом, решение задачи Коши (1) можно записать в виде матричного ряда

00 ^x(t ) = x ⁰+^ i =1

Ax ⁰( t-t ₀) ' i !

С другой стороны, разложение решений системы (1) x(t) в ряд Тейлора в некоторой окрестности точки t имеет вид:

x ( t ) ₌ x _Чg x ”⁽ t 0Х t-< о ) ' .                              (5)

Приравняем коэффициенты при одинаковых степенях в (4) и (5):

' Ax ⁰= x ⁽¹⁾(0),

A²x ⁰ = A(Ax ⁰) = x ⁽²⁾(0) ,

A n x ⁰ = A ( A n "¹ x ⁰) = x⁽ n )(0).

Отсюда получим следующую систему уравнений:

Ax₀ = x ⁽¹⁾ (0),

Ax ⁽¹⁾(0) = x ⁽²⁾(0),

Ax^{(k 4)}(0) = x^(k ) (0).

Таким образом, для нахождения матрицы получили матричное алгебраическое уравнение относительно матрицы A

AX ⁰= X ¹,                                    (6)

где матрицы X ⁰ и X ¹ определяются следующим образом:

X⁰= x ( 1 0 ), x ⁽¹⁾( 1 0 )..., x⁽ n ¹⁾( 1 0 ) , X *= x ⁽¹⁾( 1 0 ), x ⁽²⁾( 1 0 ),..., x⁽ n ) ( 1 0 ) .

Решив матричное алгебраическое уравнение (6), найдем

A = X ¹ X ^{0  1} .                                (7)

Заметим, что для построения матриц X⁰ и X ¹ будем использовать значения производных интерполяционных полиномов (3), вычисленные в точке tt .

В целом идентификация системы сводится к следующему:

• 1)    проводится интерполирование входных данных;

• 2)    строятся матрицы X ⁰ и X ¹ с использованием производных интерполяционных представлений, найденных на шаге 1;

• 3)    решается уравнение AX⁰ = X ¹.

Численные расчеты

Рассмотрим следующую задачу Коши:

r x 1( t )      3    4 x 2( t )     4    5 x 3( t )     0   0 x 4 ( t )     0   0	0    2      x 1( t ) 2   4     x 2 ( t ) 3     2     x 3( t )   , 2     1     x 4 ( t ))	x (0)	2,75 2 1,5     . 1 J	(8)
Для этой задачи можно найти точное решение:
с ' x 1( t )	1,5 + t e    1, 25 t e	t >
x 2( t )	1 t et 1 t e t	.		(9)
x 3( t )	1,5 + tet
x 4( t ))	1+ tet

Используя точное аналитическое представление решения (9), вычислим производные до 4-го порядка включительно (табл. 2). Значение функции и производные при t 0 представлены в таблице 2.

Таблица 2

j	x j (0)	x ( j 1) (0)	x ( j 2) (0)	x ( j 3)(0)	x ( j 4) (0)
1	2,75	2,25	2,75	6,25	2,75
2	2	2	2	6	2
3	1,5	2,5	3,5	4,5	5,5
4	1	2	3	4	5

В соответствии с таблицей 2 запишем значения матриц X ⁰ и X ¹ :

	r 2.75	2.25	2.75	6.25 )		r 2.25	2.75	6.25	2.75
X 0	2	2	2	6	, X 1	2	2	6	2
	1.5	2.5	3.5	4.5		2.5	3.5	4.5	5.5
	1	2	3	4 J		2	3	4	5

Согласно (7), матрица A имеет следующий вид:

	f 3.000001 4	4 5	-0.0000004 2.000001	2 4.000001
A
	-0.0000007	0.0000007	3	2
	-0.0000003	0.0000003	2	1

Видим, что данная матрица полностью совпадает с исходной матрицей с точностью до машинной погрешности. В принципе, этого следовало ожидать, так как для идентификации использовались производные до 4-го порядка, найденные из точных аналитических решений (9) (см. табл. 2).

Таблица 3

t	x 1( t )	x 2( t )	x 3( t )	x 4( t )
0,0	2,75	2	1,5	1
0,1	2,989804	2,211009	1,768273	1,215688
0,2	3,263544	2,448160	2,076385	1,465683
0,3	3,578014	2,717880	2,429746	1,754817
0,4	3,940495	3,027003	2,834467	2,088555
0,5	4,358871	3,382878	3,297442	2,473082
0,6	4,841751	3,793489	3,826450	2,915390

Рассмотрим задачу идентификации матрицы согласно изложенному подходу. Для этого, используя точные представления решения системы (9) (табл. 3), найдем интерполяционные полиномы и их производные (табл. 4).

В таблице 4 приведены производные до 4-го порядка интерполяционных полиномов при t=0:

Таблица 4

В соответствии с таблицей 4 значения матриц X ⁰ и образом:

X ¹ представляются следующим

X ⁰

X ¹

(2.75

2.249996

2.750213

6.244333 >

1.5

2.000015

2.499992

I 1

( 2.249996

1.999996

2.000015

2.499992

1.999480

6.009805

3.500324

4.492917

,

3.000145

2.750213

6.244333

3.996622)

2.843211

1.999480

3.500324

6.009805

4.492917

1.894330

5.598932

.

1.999996

3.000145

3.996622

5.053469

Таким образом, матрицу согласно формуле (7) получим в виде:

( 2.990789

-3.949929

-0.141009

2.136699 >

AP

4.007276

-5.017346

-1.976991

3.980184

-0.008410

-0.038409

2.900320

-1.904179

.

-0.004176

-0.021052

1.942604

-0.944531

j	P j (0)	P j (1)(0)	P (2) (0)	P j (3)(0)	P (4) (0)
1	2,75	2,249996	2,750213	6,244333	2,843211
2	2	2,000015	1,999480	6,009805	1,894330
3	1,5	2,499992	3,500324	4,492917	5,598932
4	1	1,999996	3,000145	3,996622	5,053469

Для матрицы AP решения системы (1), представленные с точностью 10 6 , приведены в таблице 5.

Таблица 5

t	x 1( t )	x 2( t )	x 3( t )	x 4( t )
0,0	2,750000	2	1,5	1
0,1	2,989804	2,211009	1,768274	1,215688
0,2	3,263549	2,448161	2,076388	1,465685
0,3	3,578044	2,717887	2,429764	1,754828
0,4	3,940614	3,027032	2,834537	2,088599
0,5	4,359211	3,382967	3,297644	2,473209
0,6	4,842561	3,793721	3,826925	2,915692

Сравнивание точных решений системы (8) (см. табл. 2) с решениями (табл. 5), полученными из идентифицированной системы, позволяет сделать вывод, что если решения заданы точно (замеренные с высокой точностью), то идентифицированная система, согласно предлагаемому методу, близка к исходной.

Таблица 6

t	x 1( t )	x 2( t )	x 3( t )	x 4( t )
0,0	2,750001	1,999999	1,499999	1,000001
0,1	2,989803	2,211009	1,768273	1,215687
0,2	3,263543	2,448164	2,076397	1,465690
0,3	3,577986	2,717885	2,429844	1,754846
0,4	3,940337	3,026958	2,834866	2,088628
0,5	4,358274	3,382528	3,298609	2,473157
0,6	4,839966	3,792093	3,829225	2,915222

Если же сделать допущение, что экспериментальные данные получены с некоторой погрешностью £ (табл. 6), тогда, согласно предлагаемому подходу, матрица A найдется в виде:

' 2.882199  -3.569652  -0.968181  2.915348

3.820305  -4.264691  -3.789691  5.707886

_A                                                                .

-0.001126  -0.014627  3.051067  -2.050445

-0.094601  -0.377201  1.096485  -0.139112 J

Решения системы с матрицей A представлены в таблице 7.

Таблица 7

t	x 1( t )	x 2( t )	x 3( t )	x 4( t )
0,0	2,750001	1,999999	1,499999	1,000001
0,1	2,989804	2,211009	1,768273	1,215688
0,2	3,263561	2,448196	2,076383	1,465702
0,3	3,578123	2,718132	2,429732	1,754942
0,4	3,940919	3,028008	2,834394	2,089049
0,5	4,360056	3,385767	3,297164	2,474485
0,6	4,844415	3,800240	3,825619	2,918633

Таким образом, отклонение точных решений (см. табл. 3) от решений (табл. 7) имеет незначительную погрешность, вызванную способом нахождения производных. Для повышения точности в дальнейшем предполагается использовать другие интерполяционные представления [4].

Заключение

Предложен подход к идентификации линейных стационарных динамических систем по результатам проведенных измерений фазовых координат системы на некотором промежутке времени. Идентификация матрицы системы, согласно предлагаемому подходу, сводится к построению и решению матричного линейного алгебраического уравнения (6). Построение уравнения (6) основано на сопоставлении представления решений задачи Коши в виде экспоненциального матричного ряда (4) и результатов решения задачи интерполяции исходных таблично заданных решений. Результаты численных расчетов, выполненных в среде Fortran, показывают, что идентификация системы по точным решениям задачи Коши данным подходом имеет машинную погрешность. Отклонения, превышающие машинную погрешность, связаны с точностью табличных данных и выбранного метода интерполяции полиномами Лагранжа (3), использование которых предложено для наглядности рассматриваемого подхода. Для повышения точности в дальнейшем исследовании предлагается использовать в представленном подходе как другие методы интерполирования, так и методы аппроксимации измерений фазовых координат системы на заданном промежутке времени.

Работа выполнена при финансовой поддержке РФФИ в рамках научного проекта № 12-0800309 а.