Об одном подходе к исследованию нелинейной неавтономной сингулярно-возмущенной модели динамической системы

заключается в сведении проверки условий теоремы Тихонова для модели нелинейной динамической системы к проверке аналогичных условий для ее линеаризованной модели. При этом задача решалась путем линеаризации всей исходной системы.

В настоящей работе предлагается альтернативный способ решения задачи путем линеаризации только одной подсистемы уравнений с малыми параметрами при производных (т.е. уравнений для так называемых «быстрых» переменных). Это расширяет возможности применения теоремы о предельном переходе при решении практических задач.

Условия теоремы о предельном переходе. Рассмотрим вначале подробнее условия теоремы Тихонова о предельном переходе. Пусть имеется сингулярно возмущенная модель описания процессов в нелинейной неавтономной динамической системе. Рассмотрим задачу Коши для нее:

dy - f ⁽ y, zt ) ,

> d - ^{F (} yz , ^t ) ,0 _s . . T ,       (1)

при y (0) = y , 2 (0) = Z o ,            (2)

где y = ⁽ y_x, ^ , y_n ) T , f = ⁽ f , , ^ , f n ) T - векторы n-мерного пространства, Z = ( z_x,„.,z_m ) ^T, F = ( F_x, ^ ,F_m ) ^T - векторы m-мерного пространства, ц >  0 - малый параметр.

Система уравнений (1) при заданных начальных условиях (2) соответствует модели процесса в динамической системе. Порядок этой модели k, он равен k =n+m. Если положить в (1) ц = 0 , то получим вырожденную модель :

' dy ⁼ f ⁽ y ^{г 4} ) ,

0 = F (у, z, t), 0 < t < T

,()

при у(0) = y0.(4)

Порядок системы уравнений (3) равен n, поскольку m векторных уравнений F ( ^у , — , t ) = ⁰ не являются дифференциальными. Поэтому для решения задачи Коши здесь задаются лишь n начальных условий для переменных у^ ( t ) ( i = 1, n ), совпадающих с начальными значениями из (2). Приведем формулировку теоремы Тихонова о предельном переходе [2], которая устанавливает достаточные условия близости при ц ^ 0 решения исходной задачи (1), (2) к определенному решению вырожденной задачи (3), (4) (причем для ^— это справедливо вне малой окрестности начальной точки).

Теорема. Решение полной системы (1), (2) стремится при ц ^ 0 к решению вырожденной

является точкой покоя присоединенной системы (5).

Изолированный корень z = ф ( у , t ) является устойчивым корнем в некоторой ограниченной замкнутой области D пространства ( ^у , t ) , если для всех точек ( у , t ) е D точки z = ф ( у , t ) являются асимптотически устойчивыми по Ляпунову точками покоя присоединенной системы (5). При этом под областью влияния изолированного корня ^— = ф ( у , t ) при заданных значениях у о , t о = 0 (т.е. при начальных значениях параметров у , t ) понимается совокупность таких

^—

——

точек z 0 , для которых решения z

( ^т ) присоеди-

z — ненной системы  = F (у0, z,0) с начальными dт     0       )

условиями z ( т ) = ^— ₀ ф( . у 0 ,0) .

Как отмечалось

стремятся при т ^ да к

выше, прикладной смысл

системы, если:

• 1)    корень z = ф ( у, t ) является устойчивым корнем присоединенной системы;

• 2)    начальные значения Z ₀ входят в область влияния корня Z = ф ( у, t ) при начальных значениях ^у 0 , t 0 = ⁰ •

(Изучаемое предельное равенство имеет место для всех t, для которых решение присоединенной системы лежит внутри области устойчивости ^D корня ^— = ф ( у, t ) .) Поясним смысл условий теоремы, следуя работам [2, 6]. Пусть ^— = ф ( у , t ) - одно из решений (корней) системы уравнений F ( ^у, — , t ) = ⁰ , определенное в замкнутой ограниченной области D пространства ( ^у, t ) . Корень ^— = ф ( у , t ) является изолированным , если найдется такое g >  0 , что система уравнений F ( J , — , t ) = ⁰ не имеет решений, отличных от ф ( у , t ) для || ^{z -ф (} У, t )|| <^g .

Присоединенная система определяется системой уравнений

теоремы Тихонова заключается в обосновании возможности понижения порядка сингулярно возмущенной модели процесса в динамической системе. При этом погрешность решения является величиной порядка ^ц .

Декомпозиция сингулярно возмущенной модели нелинейной динамической системы на основе уравнений первого приближения. Следуя [2], будем предполагать, что все входящие в рассмотрение функции непрерывны и все дифференциальные уравнения имеют однозначно определенные решения, и, кроме того, что функция ф ( у , t ) имеет ограниченные частные производные по всем переменным.

Введем в рассмотрение линеаризованную присоединенную систему. Для этого положим в (1) малый параметр ^ц равным нулю. Будем

предполагать,

F ( У, — , t ) = 0

что система уравнений

разрешима относительно z и

пусть z = ф ( у , t ) - один из ее корней. Подставим этот корень в остальные уравнения системы (1) и найдем соответствующее ему решение вырожденной системы (3) при начальных условиях

(4): у ( t ) , ^z ( t ) = ^{ф ( у (} t ), t ) . Знак «-» над пере-

^—

—►

у = F (у, z=, t) d т      x 7

,

в которой независимой переменной является

новая переменная т =

t

/ Ц,

а у и t рассматри-

ваются как параметры (чтобы подчеркнуть это над — пишется знак «~»). Очевидно, что корень

^— = ф ( у , t ) системы уравнений F ( ^у , — , t ) = ⁰

менными указывает на то, что решение является приближенным.

Линеаризуем уравнение Ц d f = F ( у , — , t ) в окрестности решения вырожденной системы на отрезке t 1 <  t <  T (где 1 1 - величина порядка ^ц , т.е. линеаризация осуществляется вне малой окрестности начальной точки z 0 - это связано с тем, что при переходе к вырожденной системе

начальное условие z ₀ отбрасывается). Полученное уравнение первого приближения будет иметь вид:

d A z = д F ( y , z , t ) . _д _ + д F ( y , z , t ) ^ dt        д y     L         д z

_         _     _ дф( y, t) дф(y, t) dy + v   д t        dy    dtJ

где L = L ( t ) =

= { ( y , z, t ) : y = y ( t ); z = ф ( y , t ); t_x <  t <  T } -кривая, соответствующая решению вырожденной системы;

параметром. И, кроме того, из выполнения условия 1) теоремы Тихонова для линеаризованной присоединенной системы следует, что любые начальные условия принадлежат области влияния устойчивого корня A z , ввиду линейности этой системы.

Перейдем к основным утверждениям работы, позволяющим судить о близости процессов в сингулярно возмущенной (1) и вырожденной (3) моделях нелинейной динамической системы на основе исследования свойств линеаризованной присоединенной системы (7).

Будем предполагать, что определитель

-   дF (у, z, t )| матрицы Fz =---—--- дz      IL

д F i ( y , z , t ) ^д z j

L

,     ,                        ^__

A y = y - y A z = z - z = z -ф ( y , t ) . ,;

д F ( y , z , t )

дy    l дF (y, z, t)

д _      L

д F i ( y , z , t )

.     ^д yk

" д F i ( y, z, t )

.     ^д z j

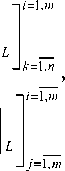
(коэффициенты матриц зависят от времени, а также от выбора корня ф уравнения ^F ( ^y , _ , t ) = ⁰ , определяющего решение вырож-

денной системы).

Переходом в (6) к новой независимой пе-

ременной

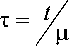
получаем линеаризованную

присоединенную систему (при этом параметр Ц в правой части кладется равным нулю):

d A z = д F ( y , z , t ) , _д _ + д F ( y , z , t ) d т      д y    ^L ^      д z

L

•A z

, (7)

в которой A y и t рассматриваются как параметры. Точка покоя линеаризованной присоединенной системы (7) является корнем уравнения

0 = 5 ^{F (} y , z , t ) •A y ₊ 5 F ⁽y•- , z , t ) •Д , д y     L          д z      L

« A , = T ( A y, t ) .

Условие 1) теоремы Тихонова для линеаризованной присоединенной системы (7) формулируется как требование, чтобы корень A , = T ( A y , t ) являлся устойчивым корнем линеаризованной присоединенной системы.

Аналог условия 2) для нелинейной присоединенной системы в линейном случае не требу-

отличен от нуля при V t е [ t 1 , T ] ( t рассматривается как параметр). Это позволяет разрешить уравнение (8) относительно A ^_ , т.е. гарантирует существование точки покоя ^A z = ^ ( А у,t ) линеаризованной присоединенной системы (7), по которой мы будем судить о свойствах нелинейной присоединенной системы (5).

Утверждение 1.

Выполнение условия 1) теоремы Тихонова для линеаризованной присоединенной системы (7) является достаточным условием его выполнения для исходной нелинейной сингулярно возмущенной модели (1).

Утверждение 2.

Пусть собственные значения матрицы Якоби F_z имеют ненулевую вещественную часть при V t е [ t 1 , T ] ( t - параметр), тогда выполнение условия 1) теоремы Тихонова для линеаризованной присоединенной системы (7) является необходимым и достаточным условием выполнения аналогичного условия для исходной нелинейной сингулярно возмущенной модели (1).

Доказательство утверждения 1.

Пусть для линеаризованной присоединенной системы (7) выполнено условие 1) теоремы Тихонова. Покажем, что при сделанном предположении о неравенстве нулю якобиана det F_z аналогичное условие будет справедливо и для нелинейной присоединенной системы (5). Рассмотрим нелинейную присоединенную систему (5) и соответствующую ей линеаризованную при-

соединенную

систему

(7). Матрица

F z =

д F ( y , z , t )

д z

Напомним, что

в системе L

переменные

(7) зависит от t .

y , A y в системах

ется, поскольку линеаризация проводится не всей модели (1), а только уравнения с малым

(5) и (7) соответственно, а также время t в обеих присоединенных системах рассматриваются как параметры.

Поскольку во всех точках кривой L ( t ) якобиан det F z ( t ) отличен от нуля, то по теореме о неявной функции [7] в некоторой окрестности каждой точки кривой L ( t ) система уравнений

' F ( ^—, y, t ) = о, ;

_ Fm (z, y, t) = 0, имеет единственное решение z = ф(y, t) . Т.о., корень — = ф(y, t) изолирован, что является обязательным условием теоремы. Далее остается показать, что этот корень есть асимптотически устойчивая точка покоя нелинейной присоединенной системы (5).

Необходимым и достаточным условием асимптотической устойчивости по Ляпунову точки покоя A z = Т ( A y , t ) линейной присоединенной системы (7) (в которой t рассматривается как параметр) является выполнение условия

Re XX t) < 0 i = 1, m I < t < T ,         ,при где Xi (t), I = 1, m, - собственные значения матрицы Fz из (7).

Обозначим через Xi (y, t) , i = 1, m, соб- ственные         значения         матрицы p   dF (y, z, t)

r, =---------- z       dz z=ф( y, t)

a F i ( y , — , t ) .     ^d z

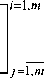
элементы которой отличаются от элементов мат- относительно области параметров D1 с D. Т.о., из выполнения условия 1) теоремы Тихонова для линеаризованной присоединенной системы (7) следует выполнение аналогичного условия и для нелинейной системы (5), что и требовалось доказать.

Перейдем к доказательству второго утверждения.

Доказательство утверждения 2.

Выполнение условия 1) для нелинейной сингулярно возмущенной модели (1) при его выполнении для линеаризованной присоединенной системы (7) следует из доказанного выше утверждения 1 и из того факта, что при асимптотической устойчивости точки покоя Az = Т(Аy,t) линеаризованной присоединенной системы (7) собственные значения матрицы Fz всегда имеют ненулевую вещественную часть.

Докажем необходимость условий утверждения 2 . Требуется показат ь , что если собственные значения матрицы F_z имеют ненулевую вещественную часть при V t e [ t 1 , T ] ( t -параметр), то из выполнения условия 1) теоремы Тихонова для нелинейной присоединенной системы (5) следует выполнение аналогичного условия и для линеаризованной присоединенной системы (7).

Пусть для нелинейной присоединенной системы (5) выполнено условие 1) теоремы Тихонова. Так как точка покоя z = ф(y, t) нелинейной присоединенной системы (5) асимптотически устойчива по Ляпунову, то согласно первому методу Ляпунова собственные значения Xi (y, t) , рицы Fz тем, что вычисляются не в точках кривой L (t), а в точках z = ф(y, t) . Очевидно, что Xi (t) = Xi (y (t), t), где y (t) - решение вырожденной системы (3).

Как показано в [8], при выполнении условия (9) в силу непрерывности X i ( y , t ) , что обес-

i = 1, m , матрицы F_z имеют неположительную вещественную часть при всех ( y , t ) e D . Поэтому и X i ( t ) = X i ( y ( t ), t ) , i = 1, m , также имеют неположительную вещественную часть. Но так как по условию утверждения Re X i ( t ) ^ 0 при

печивается непрерывностью F_z , существует область параметров y , t :

D i = { ( У’ t ) ^:| | ^{y -} y ⁽ t )|| ; t i <  t <  T } с D

(где n >  0 - некоторая постоянная), такая, что Re X i ( y , t ) <  0 при ( y , t ) e D 1 , i = 1, m (область D устойчивости корня z = ф ( y , t ) введена выше в разделе «Исходные понятия» данной статьи). Отсюда следует, что z = ф ( y , t ) является асимптотически устойчивой точкой покоя нелинейной присоединенной системы (5) равномерно

V t e [ t 1 , T ] , i = 1, m , то отсюда следует, что Re X i ( t ) <  0 при V t e [ t 1 , T ] . А значит, точка покоя ^A z = ^Т ( ^А y , t ) линеаризованной присоединенной системы (7) – линейной системы с постоянными коэффициентами ( A y и t рассматриваются как параметры) – асимптотически устойчива по Ляпунову равномерно относительно параметров A y и t .

Необходимость доказательства изолированности корня A z = Т ( А y , t ) векторного урав-

нения

d F ( y , z , t ) d y

L

•Ay +

a f ( y , z , t ) d z

—*

•Az = 0

L

отсутствует в силу его линейности. Существование же этого корня следует из сделанного предположения о неравенстве нулю определителя det F z (при V t e [ t 1 , T ] ).

Таким образом, утверждение 2 полностью доказано.

Выводы: В работе доказаны два утверждения, позволяющие судить о выполнении одного из требований теоремы Тихонова о предельном переходе для нелинейной сингулярно возмущенной модели динамической системы по уравнениям первого приближения. В частности, показано, что для асимптотической устойчивости точки покоя нелинейной присоединенной системы достаточно, а при определенных условиях также необходимо, чтобы была асимптотически устойчива точка покоя линеаризованной присоединенной системы. При этом линеаризация осуществляется вдоль траектории решения вырожденной системы.

Использование теоремы о предельном переходе предполагает также выполнение ее второго условия – принадлежности начальных значений переменных для исходной нелинейной сингулярно возмущенной модели области влияния выбранной точки покоя. Доказанные в работе утверждения позволяют сделать вывод о том, что о наличии требуемой области начальных условий для нелинейной сингулярно возмущенной модели системы, отвечающих условию 2), можно судить по ее линеаризованной присоединенной системе. Действительно, из выполнения условия 1) для линеаризованной присоединенной системы следует асимптотическая устойчивость «в малом» точки покоя нелинейной присоединенной системы и ее изолированность от других точек покоя. Это гарантирует, что требуемая область начальных условий для нелинейной модели системы будет, как минимум, конечная. Оценка же величины данной области представляет собой известную отдельную сложную задачу. Отметим только, что полученные результаты позволяют утверждать о возможности применения для ее решения второго метода Ляпунова с использованием функций Ляпунова вида квадратичной формы, построение которых всегда возможно при устойчивости линеаризованных моделей.