Об одном подходе к решению игры с «линией жизни» (случай поточечной встречи)

мится достичь «линии жизни» до момента /встречи.

Будем рассматривать игры с дискриминацией Е, в которых Е использует кусочнопостоянные стратегии ( о _а ) , а Р использует стратегии с дискриминацией из 3^ ⁺ (м).

Пусть множество S — полуплоскость

5 = {(х; у) : -х < х < +да ; у >  0}; и — некоторая фиксированная стратегия игрока Р, обладающая свойством в любой ситуации { и , у_а } е 3^⁺ х Е обеспечивать /-встречу с игроком Е во всей плоскости, если в момент времени / = 0 игроки находятся в точках z₁⁰ = (х_р 0 ; у_р 0 ), z₂⁰ = (х_Е о ; у_Е 0 ).

Обозначим через С_й ( z ⁰, z ⁰) множество всевозможных положений игрока Е в момент /-встречи в ситуации { и , У_а } для различных У_а е Е (местоположение игрока Е в момент /-встречи называется «точкой встречи»). Очевидно, что если множество С_Й ( z ⁰, z ⁰) имеет непустое пересечение с дополнением множества S, то игрок Р, используя стратегию м, не может гарантировать /встречи с игроком Е в множестве S.

Определим структуру С „ ( z ⁰, z ⁰), с тем чтобы получить уравнения границ зоны встречи и зоны убегания. Имея явное выражение для границ множества С ^ ( z ⁰, z ₂) и зная границу множества S, можно геометрически достаточно просто построить границу выигрывающего множества игрока Е в позиции Р ⁰ = z j ⁰ как множество точек z ₂ е S , для которых граница множества С ^ ( z ⁰, z ₂) касается границы множества S. Аналогично, имея явное выражение для границы С _й ( z ⁰, z ₂) и зная границу множества S, можно геометрически построить границу выигрывающего множества игрока Р в позиции Е° = z ₂ ⁰ как множество точек Zj е S, для которых граница множества С ^ ( z ⁰, z ₂) касается границы множества S.

При использовании игроками П-страте-гии граница множества С ^ ( z ⁰, z ₂) в случае поточечной поимки (/ = 0) является окружностью Аполлония [1].

Определим границу выигрывающего множества игрока Е в позиции Р ⁰ = zj = = (0; с ) (рис. 1).

Уравнение окружности Аполлония для начальных положений z j ⁰ = (0; с ), z₂ = (хе; Уе) имеет вид:

(х — Хе ) + (у — Уе ) = Х2 [х2 + (у — с) ], где X = — < 1 — отношение скоростей игро-а

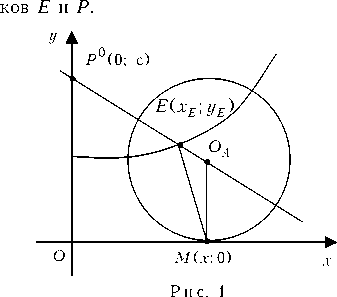
Для того чтобы окружность Аполлония касалась прямой у = 0 (границы множества S), необходимо, чтобы уравнение

( х — х_Е )² + у Е = Х ²( х ² + с ²) имело единственное решение. Для этого дискриминант приравняем к нулю:

4 х_Е ² — 4(1 — Х ²)( х_Е ² + у_Е ² — Х ² с ²) = 0.

Отсюда

- 2        „2

Уе ^хе _{= 1}

X ² c ²    (1 - X ² ) c ²

Уравнение (1) определяет границу выигрывающего множества игрока Е в позиции Р⁰ = (0; с). Искомая граница является ветвью гиперболы. Часть полуплоскости S, расположенная под этой ветвью гиперболы, является выигрывающим множеством игрока Е в позиции Р⁰.

Заметим, что абсцисса точки касания окружности Аполлония для начальных по ложений z0 = (0; с), z2 = (хе; Уе) равна х =

хЕ

Х2'

Определим границу выигрывающего множества игрока Р в позиции Е ⁰ = z ₂ = = (0; с ) (рис. 2). Уравнение окружности Аполлония для начальных положений z ₁ = (х _р ; у_р ), z ₂ = (0; с ) имеет вид:

х + ( у — с ) = Х [( х — Х р ) + ( у — Ур ) ].

Для того чтобы окружность Аполлония касалась прямой у = 0, необходимо, чтобы уравнение х + с = X [ (х — Хр) + ур ]

имело единственное решение. Для этого приравняем дискриминант к нулю:

4 Х ⁴ х_Р ² - 4(1 - Х ²)[ с ² - Х ²( х_р ² + _№²)] = 0.

Отсюда

Х ² Х р ²     Х ² _№ ²

(1 - Х ² )с ^{2 +}    с ²    = ¹

Искомая граница является верхней половиной эллипса (2). Внутренность эллипса, лежащая в полуплоскости S, является выигрывающим множеством игрока Р в позиции Е⁰.

Заметим, что в данном случае абсцисса точки касания окружности Аполлония для начальных положений Z i = (х р ; у р ), z2 = (0; с )

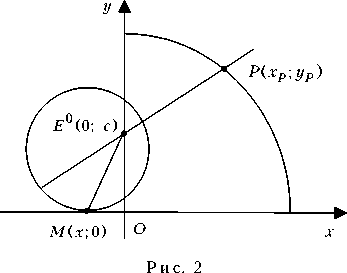
х = -

Х ²

1 -

Х ²

Х р .