Об одном подходе к решению нелинейной пространственной задачи микромеханики для однонаправленных волокнистых композитов

Расчет многослойных конструкций из композиционных материалов (КМ) требует знания механических характеристик отдельных однонаправленных слоев. Слои в составе конструкции работают, как правило, при сложном напряженном состоянии, сопротивляясь действию осевых продольных и поперечных нагрузок, а также сдвигу в продольной и поперечной плоскости. В настоящее время получено достаточно большое число решений задач микромеханики для простых условий нагружения монослоя - однонаправленного волокнистого композиционного материала (ОВКМ), позволяющих вычислить поля микронапряжений, микродеформаций и эффективные механические свойства композита [1-6]. Общая задача теории упругости о пространственном напряженном состоянии слоя при этом разделяется на три частные задачи : сдвиг в плоскости слоя (атиплоский сдвиг), продольное растяжение или сжатие и комбинированное нагружение в плоскости слоя [1,2,3]. В результате решения данных задач удается определить все эффективные упругие характеристики слоя, а также оценить его прочность при простейших условиях нагружения, используя данные о деформативных и прочностных свойствах структурных элементов. Для оценки прочности композита в услових сложного напряженного состояния используются гипотезы о преимущественных механизмах разрушения структурных элементов, определяемых в результате решения частных задач [2]. Непосредственное использование метода суперпозиций для получения решения задачи микромеханики возможно лишь в рамках линейной теории упругости. Однако уже при сравнительно небольших нагрузках в матрице или волокнах композита вследствие концентрации микронапряжений возникают зоны нелинейного деформирования или разрушения, которые и определяют его макроскопическое поведение. Численное прямое решение нелинейной пространственной задачи для неоднородного слоя весьма трудоемко. В работах [7,8] предложен оригинальный алгоритм решения пространственных упругопластических задач, возникающих при правке прокатных профилей В его основе лежит идея “расщепления” пространственной задачи на две - задачу о плоском деформированном состоянии и о продольном изгибе, с последующим итерационным решением в приращениях по шагам.

В настоящей работе для решения задачи микромеханики о произвольном пространственном нагружении ОВКМ (слоя) предлагается использовать аналогичный метод пошаговой суперпозиции с итерационным уточнением решений двух нелинейных задач - плоской задачи о произвольном трансверсальном нагружении слоя в условиях обобщенного плоского напряженного или деформированного состояния и антиплоской задачи о продольном сдвиге

хз

Рис. 1 Расчетная схема пространственной задачи микромеханики для однонаправленного волокнистого композита

Общая математическая постановка задачи заключается в решении следующей системы уравнений:

0 ; eij(f) = |(uu(f) + uJ4(n) ; Пу(г) = Сук1(кФ^Л1)£к1« ; СциСкФ.^^С^Ф,^                 11 ^п + СУгг + СЛзз;

-                                         (1)

’ ^0 ,r «Vp> где (у (г)и £ (г) - тензоры напряжений и деформаций, Q(p) и А?р)(г)- тензор упругих модулей и индикаторная функция р-го структурного компонента КМ, со(еД-функция пластичности Ильюшина, Ф - критерий прочности для матрицы Волокна принимались упругими, изотропными и неразрушаемыми Для описания нелинейного деформирования и разрушения матрицы использовались уравнения деформационной теории пластичности на участке активного нагружения и редуцирования жесткости в зонах разрушения,

С^(Ф,«,!) = '

К^цб^-б'^^ К^бцбу, Ф>0,  ^<0;

О, Ф>0, It >0

Приведенные соотношения отражают два возможных механизма поведения матрицы в разрушенных зонах: полная потеря несущей способности при 1,>0и способность воспринимать только сжимающую нагрузку в области 1, <0. Функцию пластичности Ильюшина «>(£,) строили на основе кривой 0,-е, На межфазной поверхности задавали условия полной адгезии. Граничные условия на контуре фрагмента q подбирали таким образом, чтобы напряжения, осредненные по центральной периодической ячеек, равнялись заданным макроскопическим ^ . Связь между граничными условиями и макронапряжениями можно представить с помощью соотношений [ 5]

Sy = Aykl(S )^kl                                         (3)

Начальные значения тензора корректировки граничных условий А<;н можно определить из решения трех пробных задач с единичными граничными условиями, последующие значения определяются с помощью итераций. Математические постановки задач об обобщенном плоском деформированном состоянии (рис. 1,Ь) и антиплоском сдвиге (рис. 1,с) являются частными случаями системы уравнений (1)-(2) и рассматривались ранее для расчета нелинейных полей напряжений и деформаций в однонаправленном композите в работах [ 9,10]. В результате решения первой задачи определяются следующие компоненты тензоров напряжений и деформаций

Gn(r) , (j22(f) , СГ12(г) , (У33(г),

(4) Езз(г),

8,з (?) ■                           (5)

по шагам в соответствии с к-0,1,2,...z

8и(г) , 822(г) , е12(г) , из второй задачи подлежат определению

СУ12(г) , Q33(f) , 812(?) , Макроскопические напряжения задавались условиями простого макронагружения

Sj =^ (1 + ак) , зГ^’П + аг + Жк-г)] , k=z+l,z+2,..Z.

От начального уровня ^0) до некоторого значения ^z), предшествующего первому акту разрушения, нагружение происходило с крупным шагом а, далее до заключительной точки траектории ^ , с мелким шагом р. На каждом шаге осуществлялось попарное решение плоской и антиплоской задачи в следующем итерационном цикле. Первоначально решается плоская нелинейная задача при фиксированных значениях СГ13(?) , О23(?) и 813(?) - Е23(?) принятых по результатам предыдущего шага (в исходном состоянии считаются нулевыми) Данные компоненты тензоров напряжений и деформаций используются при вычислении функции пластичности Ильюшина и критерия прочности. Полученные в результате решения плоской задачи напряжения и деформации (4) удовлетворяют не только нелинейным определяющим соотношениям (2), но и (при осреднении по центральной ячейке) соответствуют заданным макронапряжениям (3). Далее решается нелинейная антиплоская задача при фиксированных значениях компонент (4). Вычисленные таким образом £У13(г) , Q23(?) и 813(?) , 833(г) также удовлетворяют уравнениям (2) и (3). На следующем итерационном шаге снова решается плоская нелинейная задача с теми же заданными макронапряжениями § , но обновленными значениями компонент тензоров напряжений и деформаций, соответствующих продольному' сдвигу. Найденные значения компонент тензоров напряжений и деформаций (4) затем снова используются при решении антиплоской задачи. Описанная итерационная процедура повторяется до тех пор, пока отличие компонент тензора напряжений, вычисленных на двух последующих шагах, не будет меньше заданной величины. Если искомому тензору напряжений fy^r) поставить в соответствие вектор решений, определенный на конечно-элементной сетке {о}, то условие завершения итерационного процесса можно записать в виде одновременного выполнения двух неравенств:

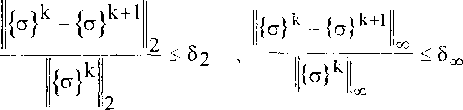
где нормы векторов определяются через компоненты вектора {□} по формулам

\ 1/2

2’1

= maxjoj

В проведенных расчетах принимались 52=0,007 , <5а, г0,05

Рассмотренная итерационная процедура используется на каждом шаге макронагружения (6). Начальные значения ^ъ выбирались таким образом, чтобы соответствующие поля микронапряжений и микродеформаций являлись упругими Величина шагов аир принималась достаточно малой (а =1.00 и 0=0.25), такой , что уменьшение шага в два раза изменяло значения напряжений в матрице и волокнах на большей части траекторий не более, чем на 5%. Нелинейные плоская и антиплоская задачи решались с помощью метода начальных напряжений.

Используя данный алгоритм, были рассчитаны диаграммы деформирования и пределы прочности однонаправленного стеклопластика при нескольких простых траекториях комбинированного нагружения растяжения или сжатия в поперечной плоскости слоя совместно с продольным сдвигом. Начальные точки траекторий s(0)y приведены в табл 1 Количество итераций при решении одной плоской или антиплоской задачи до появления зон разрушения не превышало 10, после начала разрушения в ряде случаев для сходимости требовалось до 25 итераций. Количество последовательных решений плоской и антиплоской задач на одном шаге нагружения составляло от 2 (в зоне упругого деформирования структурных элементов) до 15 (в зоне развития разрушений).

В расчетах использовался критерий прочности для матрицы (ЭДТ-10 ) в виде функции ф=P]if2 р,т, ь Рз12,/21,2+р^з1 if+p5i2'i3+рл^л +р7гг21: -1,

^сУп - 12=а,сУи ’ '^„c^a.i                            (9)

Коэффициенты Р1 рассчитывались по экспериментальным данным [11,12] Корректность вычисления коэффициентов данного критерия зависит от полноты исходных данных, при этом желательно задавать как можно больше точек , соответствующих комбинированному пространственному напряженному состоянию, экспериментальное получение которых черезвычайно трудоемко. Ввиду недостаточного количества опытных точек было вычислено пять вариантов наборов коэффициентов Р1 с различным значением прочности матрицы при гидростатическом сжатии R123: 140, 200, 400, 800 и 1500 МПа (табл.2), используемых в последующих расчетах. Для всех вариантов сечения поверхностей прочности плоскостью Оц - О|з практически идентичны и показаны для примера на рис.З штрихпунктирной линией

Таблица 1

Параметры исследованых траекторий нагружения (МПа )

Коэффициенты критерия прочности (10"2 МПа 4 )

Траектория	s,l(U)	с (0) 022	с (0) 012	с W 013	s23(0>
т,	5,0	0,0	0,0	0,0	0,0
т2	5,0	0,0	0,0	2,5	0,0
Тз	5,0	0,0	0,0	5,0	0,0
т4	2,5	0,0	0,0	5,0	0,0
т5	1,25	0,0	0,0	5,0	0,0
т6	-10,0	0,0	0,0	о,о	0,0
Ту	-10,0	0,0	2,5	о,о	0,0
т8	-10,0	0,0	5,0	о,о	0,0
т9	-10,0	0,0	10,0	о,о	0,0
Тю	-5,0	0,0	10,0	о,о	0,0
Тц	0,0	0,0	10,0	о,о	0,0

Таблица 2

R1231 МПа	Pi	Р2	Рз	Р4	.....Р.5.................	Рб	Р7
140	1,36	0,0304	-0,597	0,206	0,365	0,398	0,0911
200	1,36	-0,130	-0,504	0,074	0,472	0,334	0,0601
400	1,36	-0,317	-0,396	-0,137	0,598	0,263	0,0241
800	1,36	-0,413	-0,343	0,168	0,662	0,228	0,0063
1500	1,36	-0,448	-0,311	0,181	0,683	0,204	-0,0039

Анализ результатов расчетов показал, что диаграммы деформирования композита, соответствующие растяжению со сдвигом, являются линейными Пределы прочности для этих траекторий определялись по точке макронагружения, предшествующей процессу лавинообразного развития зон разрушения вдоль боковой стороны центральной ячейки или по межфазной поверхности, и ,как следствие, прекращение сходимости итерационных процедур Диаграммы деформирования для траекторий сжатия и сдвига (рис.2, а, б) имеют нелинейный участок, обусловленный главным образом, развитием равновесных зон разрушения Прочность композита в данном случае, как и в работах [9,10], оценивалась по условию образования в ячейке непрерывного кластера разрушенных зон, пересекающих ячейку либо вдоль одной из сторон, либо по межфазной поверхности.

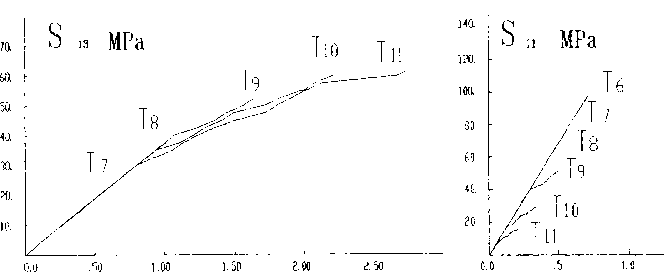
а                  Ь|з,%         б £ц,%

Рис.2 Диаграммы деформирования однонаправленного стеклопластика при комбинированном нагружении поперечным сжатием (а) и продольным сдвигом (б)

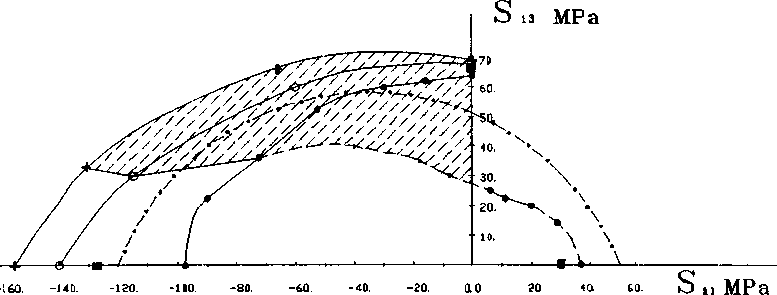
Рис.З Сплайн-аппроксимация расчетной поверхности прочности однонаправленного стеклопластика с различными коэффициентами критерия прочности для матрицы:

Ri23=200 МПа ( * ), К1?з⁼800 МПа (0),Ri₂3=1500 МПа ( + ); штриховая линия -начальная поверхность прочности композита; штрихпунктирная линия - поверхность прочности матрицы; заштрихованная область соответствует равновесному разрушению в матрице композита; ■- экспериментальные данные [13 ]

На рис 3 показана сплайн-аппроксимация построенных поверхностей прочности композита при значениях р,, отвечающих Ri23_200, 800, 1500 МПа, а также поверхность прочности матрицы для Rl23=200 МПа. Поверхности прочности для композита при Ri23 140 и 400 МПа практически совпадают с аналогичными для Rj23 200 и 800 МПа соответственно. Как видно из рисунка значение R|23 связующего, использованное при построении критерия прочности, не влияет на прогнозируемую прочность композита при растягивающих и сдвиговых нагрузках. Диапазон нагрузок, соответствующий возможному появлению зон равновесного разрушения в матрице, представлен на рис.З в виде заштрихованной области. При увеличении значения R,23 прочность композита при сжимающих нагрузках в комбинации со сдвигом увеличивается.

Заключение.

Предложенный метод решения нелинейных задач микромеханики в объемной постановке совместно с методом локального приближения позволяет прогнозировать деформационные и прочностные характеристики ОВКМ при любых условиях продольно-поперечного нагружения и дает возможность построения полной поверхности прочности композита.