Об одном решении задачи построения динамической математической модели отопительных приборов и систем

В нашей стране на теплоснабжение зданий расходуется более одной третьей всего добываемого топлива, причем основными при этом являются затраты на отопление. В связи с этим возникает задача разработки комплексных подходов и решений по рациональному использованию расходуемых на эти цели энергетических ресурсов. Такие комплексные решения должны включать в себя, очевидно, следующие составные части: выбор наиболее эффективных с точки зрения теплозащиты конструкций зданий, грамотные градостроительные и планировочные решения по застройке, эффективные схемы систем теплоснабжения и отопления зданий, а также гибкие и надёжные системы автоматического управления процессами теплоснабжения. Причем известно также, что наибольшая экономия тепловой энергии достигается за счет автоматизации систем отопления. Поэтому разработка вопросов, связанных с автоматизацией систем отопления и их совершенствованием, является вполне актуальной проблемой. При этом следует иметь в виду, что первоочередной задачей, которую необходимо решать при разработке высококачественных систем управления, является создание соответствую- щего математического и программного обеспечения, в частности, динамических математических моделей отопительных приборов и систем и алгоритмов их параметрической идентификации. Объясняется это тем, что как сама структура системы управления, так и параметры ее настройки определяются, прежде всего, свойствами и характеристиками объекта управления, которые, в частности, и представляются их математической моделью. Вместе с тем, эти свойства и характеристики заметно меняются, например, из-за старения системы отопления, в частности, из-за ее загрязнения, из-за достаточно хаотического процесса по замене отопительных приборов в части помещений и квартир, из-за использования декоративных панелей для отопительных приборов и т. п. Поэтому вполне понятно, что необходимо своевременно отслеживать изменение этих характеристик, т. е. решать задачу структурной и параметрической идентификации математической модели.

Синтез структуры математической модели

Известно, что теплота, доставляемая теплоносителем отопительному прибору, может быть вычислена по следующей формуле:

Q = C m G m ( t ВХ ^- t ВЫХ ), U)

где С_m – удельная теплоемкость теплоносителя, G_m – массовый расход теплоносителя через прибор, t _ВХ и t _ВЫХ – соответственно температура теплоносителя на входе и выходе из отопительного прибора.

Часть этого количества теплоты к ПР F _np( t _Т - t В ) будет передана отопительным прибором внутреннему воздуху помещения, а оставшаяся часть С т G m ⁽ t ВХ ^- t ВЫХ ) ^- k ПР ^F nP ⁽ t Т ^- t В ) пойдёт на ^изменение температуры теплоносителя и самого отопительного прибора. Здесь k _ПР – коэффициент теплопередачи отопительного прибора, F _ПР – его площадь поверхности теплообмена, t _Т – средняя температура теплоносителя в отопительном приборе (или, что то же самое – средняя температура металла отопительного прибора), t _В – температура воздуха в помещении. Поэтому, следуя [1], уравнение теплового баланса запишем следующим образом:

C ПР “ТТ = C m G m ⁽ t ВХ ^- t ВЫХ ) ^- d т

^- k ПР ^ ПР ⁽ t Т ^- t В ), ⁽²⁾

каналу «температура теплоносителя на входе в отопительный прибор – средняя температура теплоносителя в отопительном приборе», к ₂ =----^^Пр^^Пр---- —

2 C m G m + к ПР F np

коэффициент передачи по каналу «температура внутреннего воздуха – средняя температура теплоносителя в отопительном приборе». Как видно из приведенных соотношений, с увеличением расхода теплоносителя через прибор G_m его посто-

янная времени T уменьшается, следовательно, уменьшается и инерционность переходных процессов в приборе, одновременно уменьшается и коэффициент передачи k ₂ , т. е. уменьшается

влияние температуры внутреннего воздуха на среднюю температуру отопительного прибора. Поскольку при этом -дк^ = 2CmknpFnp  > 0, dGm (2CmGm + кПРFnP )

где С ПР = С т р т ^VПР ⁺ С м m _м

–

полная теплоем-

кость отопительного прибора вместе с находящимся в нем теплоносителем, р _m - плотность теплоносителя, V _ПР – объем теплоносителя в отопительном приборе, C _м – удельная теплоемкость металла отопительного прибора, m м – масса отопительного прибора, т - время.

Известно, что средняя температура теплоносителя в отопительном приборе может быть выражена t т =(t вх + t вых V2, (3) поэтому tВЫХ = 2tТ -tВХ. Подставляя данное соотношение в (2) и переписав его соответствующим образом, получим, что структура динамической математической модели отопительного прибора будет иметь вид:

то с увеличением расхода теплоносителя через прибор G_m коэффициент передачи k ₁ растет, что свидетельствует об увеличении влияния температуры теплоносителя на входе в отопительный прибор на его среднюю температуру.

С увеличением произведения коэффициента теплопередачи отопительного прибора на его площадь поверхности k _ПР F _ПР коэффициент передачи k ₁ однозначно уменьшается, а k ₂ однозначно

растет, так как

д к ₂

2 C m G m

^{д ( к} ПР ^F nP ) ⁽² C m G m ^{+ к} ПР ^F nP ) 2

> 0,

т. е. увеличивается влияние температуры внутреннего воздуха на среднюю температуру отопительного прибора, а влияние t _ВХ ослабевает. Влияние k _ПР F _ПР на постоянную времени T не так очевидно, так как с увеличением F _ПР знаменатель выражения

^C ПР

² C m G m ^{+ к} ПР ^F nP

растет, однако и числитель

ПР

dt _Т

2 C m G m + к пр ^ пр d т

2 CG

+1т =

С ПР = С т р m V np + С м m м тоже растет из-за увеличения массы прибора m м и его объема V ПР , поэтому все зависит от того, что растет быстрее – числитель или знаменатель. Если же при постоянных значениях F ПР , его массы m м и объема V ПР каким-то образом увеличивается k _ПР , то растет только знаме-

mm t

2C m G m + к np F np ВХ

^k ПР ^F ПР

2 C m G m + к ПР ^

t _В . (4)

Перепишем данное уравнение, используя стандартные для теории автоматического управления обозначения [2]:

натель выражения T =-------^П------ , поэтому ² C m G m ^{+ к} ПР ^F nP

T ^Т + t Т = ^к 1 t ВХ ⁺ k 2 t В . d т

постоянная времени T будет уменьшаться.

В целом, все вышеизложенное согласуется с простыми физическими соображениями, что свидетельствует, по меньшей мере, о качественной адекватности математической модели.

Здесь T =

C _ПР

2 C m G m + к ПР F 1P

– постоянная времени,

к =--- ^m^m ---- - коэффициент передачи по

2 C m G m + к ПР F np

Проведение эксперимента

Экспериментальная установка представляет собой одиннадцатисекционный чугунный радиатор с односторонним подключением и движением теплоносителя «сверху-вниз». Для регулирования

Инженерное оборудование зданий и сооружений

расхода теплоносителя через отопительный прибор на подающей подводке установлен вентиль ручной регулировки, кроме того, на подающей и обратной подводках установлены шаровые краны. При проведении эксперимента температура на поверхности прибора измерялась с помощью пирометра «Optris Minisight». Показания снимались в 8 экспериментальных точках: на подающей и обратной подводках и в центрах 1, 3, 5, 7, 9 и 11-й секций радиатора. Экспериментальные точки представляют собой очищенные от краски участки радиатора и труб. Температура внутреннего воздуха помещения измерялась с помощью термоанемометра АТТ-1004 «Актаком» в 4-х точках: непосредственно над отопительным прибором, над отопительным прибором на высоте 3 метра от пола, в центре помещения на высоте 1 метр от пола, в центре помещения на высоте 3 метра от пола. Расход теплоносителя измерялся накладным ультразвуковым расходомером Portaflow PF330.

Схема экспериментальной установки приведена на рис. 1.

В течение первых 2 часов эксперимента данные снимались через каждые 10 минут. Далее по причине слабой переменчивости данные снимались только каждые 30 минут и так до окончания эксперимента.

Параметрическая идентификация модели

Задача параметрической идентификации математической модели (5) формулировалась как

следующая задача оптимизации:

^T к

I = I ^T

0 L

dt

T + t Э dτ

- kt ЭХ

- k 2 t Э

d ^{T >} min , (6)

T,k ₁ ,k ₂

ЭЭ Э где tT ,tВХ ,tВ – соответственно экспериментальные значения средней температуры отопительного прибора, температуры теплоносителя на входе в отопительный прибор и средней температуры воздуха в помещении, тк - время проведения экспе-

римента.

Данная задача решалась методом покоординатного спуска со встроенным методом «золотого сечения», в результате решения были найдены численные значения параметров математической модели, так, в частности, по результатам процесса нагрева постоянная времени T = 3126 с, коэффициент передачи к 1 = 0,624 ° C/ ° C, коэффициент передачи к ₂ = 0,829 °C/° C.

На рис. 2 приведена расчетная кривая t _T ( т ) , вычисленная по уравнению (5) при указанных значениях его параметров, там же крестиками показаны экспериментальные точки. Как видно из рис. 2,

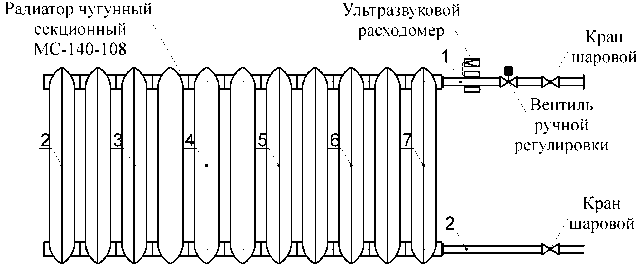
Рис. 1. Схема экспериментальной установки

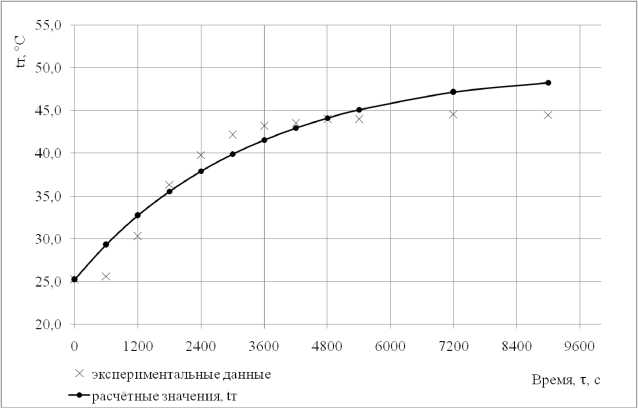
Рис. 2. Расчетные и экспериментальные значения средней температуры отопительного прибора в процессе нагрева

качество настройки математической модели на экспериментальные данные вполне удовлетворительное.

В заключение отметим, что, как известно (см., например, [3]), систему отопления в целом можно представить эквивалентным отопительным прибором, поэтому все вышеизложенное может быть применено и к построению математической модели всей системы отопления здания.

Выводы

Предложена структура математической модели отопительных приборов и систем. Оценена качественная адекватность модели. В результате решения задачи параметрической идентификации показано, что найденная структура математической модели и количественно удовлетворительно настраивается на экспериментальные данные. Поэтому модель может быть использована для изуче ния особенностей нестационарных процессов в отопительных приборах и системах, а также при разработке систем автоматизации отопительных установок.