Об одном решении задачи построения общей модели теплового режима здания и его системы отопления

Постановка задачи

Как известно, задача построения математической модели любого объекта управления обычно делится на две части:

• 1)    синтез структуры математической модели;

• 2)    определение параметров (коэффициентов) математической модели.

Каждая из этих подзадач решается неоднозначно, так как, в частности, принятые допущения, а также физические эффекты и явления, учтенные при структурном синтезе математической модели, могут быть неодинаковыми, следовательно, в итоге получаются и различные структуры моделей. Критерии количественной близости модели и объекта также могут быть разными, что приводит к разным численным значениям параметров модели одной и той же структуры.

В работах [1–3] определена и обоснована структура математической модели теплового режима зданий (ТРЗ). Основным использованным при этом допущением является предположение о квазистационарности процесса переноса теплоты через толщу наружного ограждения. Однако на самом деле температурное поле в ограждении обычно является нестационарным, поэтому интересно было бы выяснить, какая математическая модель теплового режима здания получится в этом случае, т. е. в случае учета нестационарности реального температурного поля. Данная задача и рассматривается в настоящей работе.

Синтез структуры модели ТРЗ

Следуя [4], температурное поле в наружном ограждении здания опишем одномерным уравнением теплопроводности д t (х, т)     д21 (x, т) n r n

• —= a —^^, 0 < x < L , т> 0,                                           (1)

дт        дx2

где t ( x , т ) - температура в точке с координатой x по толщине стены здания в момент времени т ; а - эквивалентная температуропроводность материала стены [4]; L - толщина стены здания.

Температура в любой точке стены в начальный момент времени задается уравнением t (x,0) = t0(x), 0 ^ x ^ L,                                                                             (2)

где t ⁰( x ) – заданная функция.

Теплообмен на внутренней и наружной поверхностях ограждения описывается граничными условиями третьего рода:

^_Л 5 t (О, ^{т )}     = ^а в [ t в ^{( т} ) _ t ^{(0, т )} ] , ^т > 0;

^{д x}    x = 0

д t ( L , т )

• Л----------

x = L

= а н [ t ( L , т ) - t н ( т ) ] , т> 0,

где а _в, а _н - коэффициенты теплоотдачи для внутренней и наружной поверхностей ограждения;

t _В, t _Н – соответственно температура внутреннего и наружного воздуха.

Проинтегрируем уравнение (1) по координате x в пределах от 0 до L и разделим обе его части на L , тогда получим dt = а дt(L, т)   дt(0, т)

d т  L дx дx где t = — J t(x, т) dx - среднее значение температуры стены.

L ₀

Если предположить, что ограждение можно приближенно считать термически тонким телом, то уравнения (3) и (4) можно переписать в виде:

^^М = _ав [ t в ( т ) _ Г ] ;                                                    (6)

д x

^_Л д ,    = ^а н [ t ^_ t н^{( т )} ] .

д x

Тогда уравнение (5) можно представить следующим образом dt = a Г^ ( Г _ t н(т)(t в(т) _ Т, ^ d т L L Л              Л_

L Л       d t —     Отт              op     _z _

—--------- • —+ t =--------t н(т) +--------t в(т).

а ( а _н + а _в) d т     а _н + а _в        а _н +а _в

Если в формуле (8) множитель перед производной обозначить следующим образом

Т1 = ( LЛ . ,(9)

а ( а _н + а _в)

то уравнение (8) перепишется так:

dt -     ан      , . ав , ._

Т1 — + t =---------t н(т) +---------t в(т).

d т     а _н + а _в       а _н +а _в

Далее запишем уравнение теплового баланса для бесконечно малого промежутка времени d т :

с в m в dt^ = W(т) _ав [ t в(т) _ t")] fct _ kОК FOK[ t в(т) _ t н(т)], d т где cВ, mВ – соответственно удельная теплоемкость и масса воздуха в здании; FСТ, FОК – площадь стен и окон здания; к0К - коэффициент теплопередачи окон; W(т) - мощность системы отопления.

Выполнив для уравнения (11) ряд математических преобразований, получаем

Управление в технических системах сВmВ

•

^а В F CT + k ОК F OK

+     ав FCT аВFCT +kOKFOK

dt В (т) +tВ (т) =---------1--W (t) + dт          аВFCT +kOKFOK

- t +---- k oK F oK----- t _Н( т ).

^а В F CT ⁺ k OK F OK

Если в формуле (12) обозначить, что

Т =     с В m В аВ FCT + kOK FOK то уравнение (12) можно представить в виде

Т 2 • d B^ + 1 В ( т ) =-------- ¹ W ( t ) +-----^ В F ^C----- t +---- k OK F OK---- 1 Н ( t ) .

d ^т           а В F CT ⁺ k OK F OK        ^а В F CT ⁺ k OK F OK    ^а В F CT ⁺ k OK F OK

Таким образом, сводя предыдущие выкладки воедино, получаем систему уравнений вида:

_ dt -     ан . .     aR . .Т! — + t =--------th(t) +--------tв(т);

d т     аВ + аН      аВ + аН

7 (0 ) = 7 ⁰;

Т 2 • dt ^r) + 1 В ( т ) =------- 1 W ( т ) +---- ^{a F} ----7 +---- k oK F oK---- t _Н( т );

^{d т          а} В F CT ⁺ k OK F OK        ^а В F CT ⁺ k OK F OK    ^а В F CT ⁺ k OK F OK

1 1 В ( 0 ) = t В .

Графически полученная структура математической модели теплового режима здания может быть представлена с помощью алгоритмической структурной схемы (рис. 1). Здесь p – оператор дифференцирования.

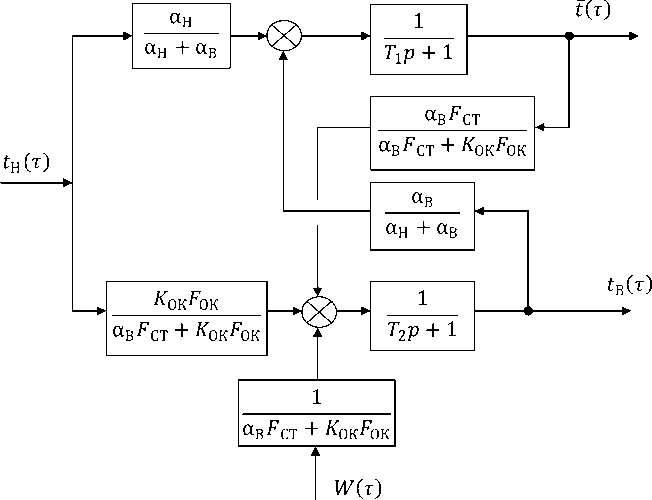
Рис. 1. Алгоритмическая структурная схема модели ТРЗ

Математическую модель (15) можно представить в виде одного дифференциального уравнения 2-го порядка. Для этого из третьего уравнения системы (15) выразим среднемассовую температуру t :

- ^аВ F CT ⁺ k OK F OK t =--

^а В F CT

T2 dt^ +1В1-------WkOKFOK---- d т      аВ FCT + kOK FOK    аВ FCT + kOK FOK

а также найдем ее производную по т :

dt

d т

^а В F CT + k ОК F OK а в F cT

T 2

d ² t _В dt _В         1         dW      k _ОК F _ОК      dt _Н

+----*---*

d ^т    d ^{т  а} в F CT + k OK F OK d ^{т a} B F CT + k OK F OK d ^т

и подставим эти соотношения в первое уравнение системы (15). Выполнив необходимые математические преобразования, получим, что математическая модель теплового режима зданий представляется следующим дифференциальным уравнением 2-го порядка:

T . T 2 d^ B + ( T 1 + T 2 ) dt H + ₁ В = d т ²            d т

^a B F CT

^(а В + ^а н ) ^(a B F CT + к OK F OK )

t в +-- ^a B F CT ⁺ k OK F OK

T W + W ( т ) | + d т        )

k ОК F ОК      dt Н

1 .-+ ^а В F CT ⁺ k OK F OK ^{d т}

---kOKFOK---+-------^B^HFCT-------- vaB FCT + kOK FOK (aB +aH ) (aB FCT + kOK FOK ))

t Н .

Анализ уравнения (18) показывает, что объект моделирования как по каналу «мощность сис- темы отопления – температура внутреннего воздуха», так и по каналу «температура наружного воздуха – температура внутреннего воздуха» описывается дробно-рациональными передаточными функциями, степень полиномов числителей которых равна 1, а знаменателей – 2.

Модель системы отопления

Поскольку в алгоритмической структурной схеме TP3 есть вход, обозначенный как W ( т ) -мощность системы отопления, то для полного решения задачи моделирования необходимо построить модель системы отопления здания. Данная задача решалась в работах [5–7] как для стационарного, так и для динамического случаев. Динамическая модель системы отопления приведена в работе [7], ее алгоритмическая структурная схема, представлена на рис. 2.

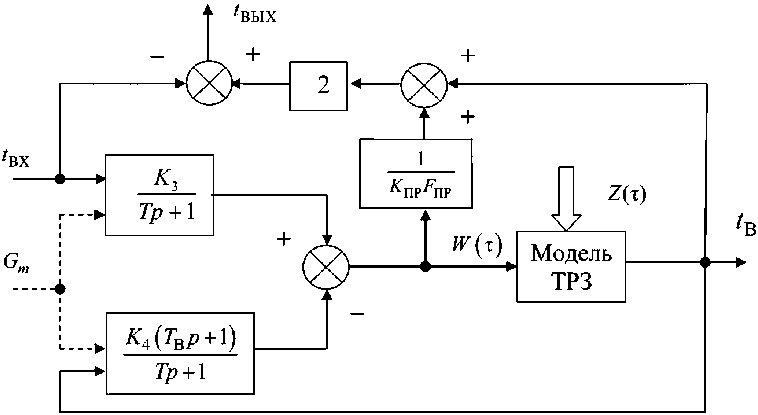
Рис. 2. Алгоритмическая структурная схема модели системы отопления

На рис. 2 Z ( т ) - вектор возмущающих воздействий TP3, основным из которых является t _Н -температура наружного воздуха, сплошными линиями обозначены сигнальные воздействия, а штриховыми – параметрические, т. е. воздействия, определяющие численные значения параметров (коэффициентов) модели.

Поскольку теплоотдача (мощность системы отопления W ( т )) зависит от температуры внутреннего воздуха t _В , то структурная схема включает модель ТРЗ. В результате видно, что математическая модель системы отопления вместе с моделью ТРЗ составляют замкнутую систему уравнений, полностью описывающую поведение объекта управления, который в данном случае включает систему отопления и собственно ТРЗ. Входными величинами для данного объекта являются температура теплоносителя на входе системы отопления t _ВХ( т ) , расход теплоносителя через систему отопления G m ( т ) и вектор возмущений TP3 Z ( т ). Выходные величины объекта -

Управление в технических системах это мощность (тепловой поток) системы отопления (эквивалентного отопительного прибора) W(т), температура внутреннего воздуха tВ (т) и температура обратной воды (на выходе системы отопления) tВЫХ (т).

Адекватность моделей ТРЗ и СО оценена в работах [2–3, 5–7]. Показано, что разработанные структуры моделей допускают удовлетворительную настройку на «реальный процесс». При этом применялись разные подходы и различные процедуры решения задачи идентификации. Например, при прямом решении задачи, когда мерой количественной близости модели и объекта моделирования является квадрат или модуль невязки между правыми и левыми частями уравнений, в которые подставлены экспериментальные данные, требуется вычислять производные сигналов температуры внутреннего и наружного воздуха, а также и сигнала мощности СО. Как это хорошо известно, задача дифференцирования сигналов является некорректной, поэтому необходима определенная проработка конкретного способа реализации процедуры дифференцирования. Здесь представляется целесообразным использовать следующий алгоритм [3].

Пусть средняя величина сигнала в ( i + 1) -й момент времени определена по четырем точкам, т. е.

x = ⁽ x i + 1 ⁺ x ⁺ x i — 1 ⁺ x i - 2^)/4 .                                                                        ⁽¹⁹⁾

Отнесем x к середине временного интервала, на котором располагаются рассматриваемые точки, т. е. картина расположения точек будет такой, как это представлено на рис. 3.

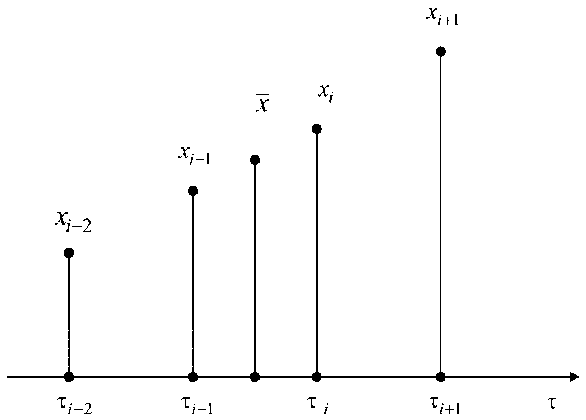
Рис. 3. Расположение точек, используемых при дифференцировании

Очевидно, что в этом случае можно пользоваться следующими четырьмя оценками производной:

dx ^{( т} i + 1⁾ ^ x i + 1 ^{- x} ;

d т      1,5 Ат ’

dx(тi+1) xi - x dт    0,5Ат ’ dx (т i+1) x - xi-1

d т      0,5 Ат ’

^{dx ( т} i + 1⁾ _ ^{x - x} i - 2

d т      1,5 Ат

Здесь Ат - промежуток времени между моментами считывания сигналов Ат = т i _{+ 1} - т i , i = 0,1,2, .„

Понятно, что лучшей оценкой будет среднее арифметическое найденных величин, т. е.

dx ( τ _{i + 1}) =_[ d τ

x i + 1

-

xx + ⁱ

-

xx +

-

x i - 1 + x - x i - 2

1,5 Δτ    0,5 Δτ    0,5 Δτ     1,5 Δτ

]/4 =

=    [ ( x_{i + 1} - x ) + 2( x_i - x ) + 2( x - x_{i - 1}) + ( x - x_{i - 2})]/4 =

Δτ 33

11         11

x_{i - 1}) + ¹ ( x - x_{i - 2})] = 6

=     [ ( x_{i + 1} - x ) + ( x_i - x ) + ( x -

Δτ 6          22

= ¹ [( x_{i + 1} - x ) + 3( x_i - x ) + 3( x - x_{i - 1}) + ( x - x_{i - 2})] = 6 Δτ

= 1 [ x_{i + 1} + 3 x_i - 3 x_{i - 1} - x_{i - 2}].

6 Δτ

Данная формула для вычисления производных применяется в составе адаптивного алгоритма идентификации параметров, в том числе и коэффициента передачи по каналу «мощность систе мы отопления – температура внутреннего воздуха» kП =               . На рис. 4 приведены

αВFСТ + kОКFОК кривые, иллюстрирующие процедуру отслеживания параметра kП как при отсутствии, так и при наличии помех в исходных данных. При этом истинное значение коэффициента передачи kП со- ставляло 3,103 ⋅10

⁵ °C/Вт . Начальные значения параметра k _П , как это видно из рис. 2, составля-

ли 2 ⋅ 10

⁵ °C/Вт и 4 ⋅ 10

⁵ °C/Вт, причем начальное значение k _П = 2 ⋅ 10

5 °C/Вт исправлялось как

по данным без помех, так и по данным с помехами.

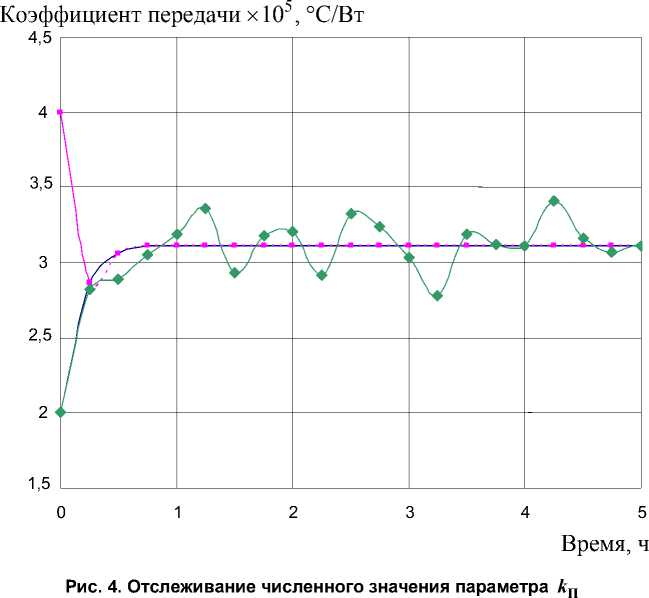
Как видно из рис. 4, коэффициент передачи k _П исправляется с помощью адаптивного алгоритма в целом достаточно быстро, только при наличии помех в экспериментальных данных наблюдается некоторое колебание его текущего значения вблизи истинного значения k _П = 3,103 ⋅ 10 ^{- 5} °C/Вт.

Управление в технических системах

Для большей точности оценки параметра k _П в схему обработки экспериментальных данных помимо помехоустойчивого алгоритма дифференцирования (24) включили еще и предварительный алгоритм фильтрации сигнала о температуре внутреннего воздуха.

Задача фильтрации сводилась к следующей задаче оптимизации:

У 1⁽ x i - ^{х ф )}2 + У 2^{( Х} Ф - x ^)² ^ m i n,                                                      ⁽²⁵⁾

xiФ где xi – фактическое значение сигнала в i -й момент (отсчет), xiФ – оценка полезного сигнала для i -го момента времени, у1 и у2 — весовые коэффициенты.

Решая данную задачу оптимизации, нашли, что оптимальная оценка полезного сигнала должна определяться по следующей формуле

, ф

Ф   У 1 x i +y 2 x i - 1

.

x i =--------;--------

У1 + у 2

Удобно данное соотношение записать в следующем виде

Ф Ф ₊ ^У 1 (г y Ф x i = x i - 1 ⁺ ---------- ⁽ x i x i - 1 ).

Wl+W2

Данный алгоритм позволяет отслеживать изменение полезного сигнала во времени. Как видно из последнего уравнения, если сигнал не изменился за промежуток времени между ( i - 1) -м

• и i -м моментами, то оценки х ^Ф и х ^Ф 1 будут совпадать.

Для примера на рис. 5 приведены кривые, иллюстрирующие работу алгоритма: кривая 1 – это оценка параметра k _П при отключенном алгоритме фильтрации (27), кривые 2 и 3 – оценки, найденные с включенным алгоритмом фильтрации соответственно для у 1 = 0,3; у 2 = 0,7 и для у 1 = 0,1; у 2 = 0,9. Кривую 1 можно рассматривать как оценку, найденную для у 2 = 0 .

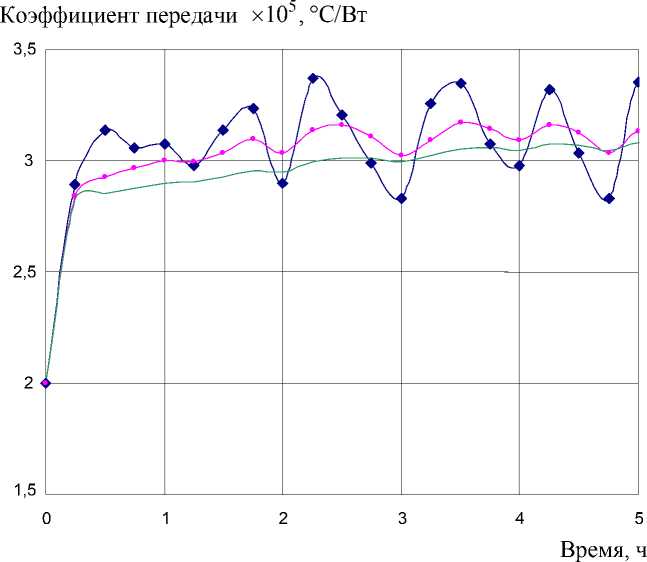
Рис. 5. Отслеживание численного значения параметра k _П при использовании алгоритма фильтрации

-1

-2

-3

Как видно из рис. 5, алгоритм (15) обладает заметными фильтрующими свойствами. При этом, как и следовало ожидать, уменьшение у1 и увеличение у2 приводит к усилению фильт- рующих свойств алгоритма. Отклонение получаемых оценок от истинного значения kП заметно уменьшается. В наших расчетах это отклонение всегда удавалось за счет настроек алгоритма фильтрации (за счет выбора ψ1 и ψ2 ) довести до допустимого значения. Таким образом, дополнительное использование алгоритма фильтрации позволяет получить вполне работоспособную процедуру оценивания коэффициентов модели.

Выводы

Рассмотрено решение задачи структурной идентификации общей математической модели теплового режима здания и его системы отопления. При этом в модели ТРЗ учтена нестационар-ность температурного поля по толщине его наружного ограждения. Приведены данные по параметрической идентификации, в частности, по решению подзадачи дифференцирования используемых при этом экспериментальных сигналов. Настроенная на «реальный процесс» математическая модель может быть использована как для исследования особенностей режимов работы СО и ТРЗ, так и для разработки высококачественных управляющих устройств, в частности, для настройки погодного регулятора отопления.