Об одном способе аппроксимации производных в гексаэдрических 8-узловых конечных элементах

Автор: Чекмарев Д.Т., Глазова Е.Г., Абу Даввас Я.

Журнал: Вестник Пермского национального исследовательского политехнического университета. Механика @vestnik-pnrpu-mechanics

Статья в выпуске: 6, 2024 года.

Бесплатный доступ

При численном решении задач теории упругости и пластичности часто используются конечные элементы с сокращенным интегрированием, особенно при решении динамических задач. В этом случае для 8-узловых трехмерных элементов вместо 8 точек численного интегрирования используется одна. При этом фактически принимается, что деформации и напряжения являются постоянными в пределах элемента. В этом случае не является необходимой традиционная техника построения матрицы жесткости для элемента стандартной формы в виде куба с последующим отображением фактических конечных элементов произвольной формы и размера на стандартный. Вместо этого матрицу жесткости можно строить непосредственно для конечного элемента произвольной формы. В данном случае она выражается через коэффициенты сеточных операторов, аппроксимирующих первые частные производные поля перемещений в конечном элементе. В работе рассматривается новый подход к аппроксимации производных при построении матрицы жесткости для трехмерного 8-узлового конечного элемента с одной точкой интегрирования. Теоретической основой данного подхода является дальнейшее развитие класса ажурных схем МКЭ. Полученные формулы позволяют строить несовместные схемы МКЭ с улучшенными свойствами. В работе обсуждаются проблемы неустойчивости типа «песочные часы», сдвигового и объемного запирания. Предлагается новый эффективный подход к решению проблемы «песочных часов». Также обсуждается возможность применения новых формул аппроксимации производных к конечным элементам вырожденной формы с числом узлов меньше восьми. Показано, что они остаются применимыми стандартным образом и в этом случае. Результаты исследования подтверждаются приведенными результатами численного решения модельных статических задач теории упругости.

Еще

Трехмерная задача, метод конечных элементов, ажурная схема мкэ, моментный конечный элемент, неустойчивость типа «песочные часы», сдвиговое запирание, аппроксимация производных, разностная схема уилкинса, матрица жесткости, вырожденные элементы

Еще

Короткий адрес: https://sciup.org/146283072

IDR: 146283072 | DOI: 10.15593/perm.mech/2024.6.07

Текст научной статьи Об одном способе аппроксимации производных в гексаэдрических 8-узловых конечных элементах

ВЕСТНИК ПНИПУ. МЕХАНИКА № 6, 2024PNRPU MECHANICS BULLETIN

Традиционная техника метода конечных элементов состоит в построении матрицы жесткости для элемента стандартной формы и размера (квадрат в двумерном случае, куб в трехмерном случае), а в дальнейшем используется отображение произвольного конечного элемента произвольной формы на стандартный элемент. В результате матрица жесткости конечного элемента также преобразуется. Для конечных элементов в форме симплекса с линейной аппроксимацией функций (двумерного треугольника или трехмерного тетраэдра) техника отображения как правило не используется (см. [1]). Это связано с тем, что в данном случае отображение является линейным, якобиан отображения – постоянным и для интегрирования достаточно одной точки. Поэтому матрицы жесткости элементов произвольной формы строятся непосредственно в процессе решения задачи. При этом элементы матрицы жесткости выражаются через коэффициенты операторов сеточного дифференцирования, аппроксимирующих первые производные неизвестных функций в элементе. При решении динамических задач теории упругости и пластичности на базе явных схем интегрирования по времени часто используются 4-узловые двумерные или 8-узловые трехмерные конечные элементы с неполным интегрированием, когда вместо 4 гауссовых точек интегрирования в двумерном элементе или 8 точек интегрирования в трехмерном используется одна точка. В этих случаях задача отображения произвольного конечного элемента на элемент стандартной формы фактически эквивалентна построению операторов численного дифференцирования на 4-узловом или 8-узловом шаблоне произвольной формы. В известной разностной схеме Уилкинса [2], эквивалентной схеме МКЭ с одной точкой интегрирования, матрица жесткости не строится, а вместо этого формируются соответствующие дифференциальные операторы. Матрица жесткости конечного элемента записывается в виде [3]: K = jBTCBdV , где Э

В – матрица деформаций, связывающая компоненты тензора деформаций с узловыми перемещениями, С – матрица упругих постоянных. В общем случае элементы матрицы В являются функциями пространственных координат, но для линейных конечных элементов в виде симплексов, а также для элементов с одной точкой интегрирования они являются константами. В этом случае матрица жесткости принимает вид K = B^T CB Д V, где Δ V – объем элемента. Ненулевые элементы матрицы В являются коэффициентами сеточных операторов, аппроксимирующих первые частные производные в элементе. Данные операторы могут быть представлены в виде

m di f = £ вЛ=дт + O (h). (1)

j = 1 о x

Здесь m – число узлов в элементе, fj – значения функции в узлах элемента, вj - коэффициенты разностных операторов. Таким образом, элементами матрицы B являются коэффициенты вj и задача построе- ния матрицы жесткости фактически сводится к определению этих коэффициентов.

Отметим еще один важный аспект построения численных схем МКЭ, рассмотренный в данной работе. Это борьба с двумя нежелательными эффектами, присущими многим конечным элементам – эффектами сдвигового и объемного запирания и неустойчивости типа «песочные часы». Оба эти эффекта давно известны, по ним имеется обширная литература [4–10], но актуальность их исследования не пропала, о чем свидетельствуют появляющиеся до последнего времени публикации, например [11–13]. Эффект запирания присущ многим элементам низкого порядка (с линейной и полилинейной аппроксимацией неизвестных функций) и связан с неудовлетворительной аппроксимацией конечным элементом деформаций изгиба (сдвиговое запирание) либо в случае почти несжимаемых сред (объемное запирание). Следствием этого является медленная сходимость численных решений. Для борьбы с данным эффектом применяется сокращенное интегрирование, а также применение элементов более высокого порядка и измельчение сетки, что приводит к значительному увеличению вычислительных затрат при решении задач. Эффект «песочных часов» связан с наличием в элементах мод нулевой энергии, когда конечный элемент не реагирует на некоторые изменения его формы (типичный случай – на изгиб и кручение). Иначе это можно интерпретировать как «неполноту» системы сеточных операторов. Так, если в энергии элемента учитываются только первые производные поля перемещений, то пересечение ядер операторов (1) будет ненулевым и включать в себя деформации изгиба и кручения элементов. Для борьбы с данным видом неустойчивости используются различные искусственные приемы [13; 14]. Неустойчивость типа «песочные часы» присуща элементам с неполным интегрированием. Отметим, что у линейных элементов, в частности у 4-узлового тетраэдра, «песочные часы» не проявляются, поскольку в данном случае пересечением ядер операторов (1) является смещение тела как жесткого целого, которое ликвидируется при наличии в задаче кинематических граничных условий.

Формулы аппроксимации первых частных производных

Аппроксимация производных в конечном элементе произвольной формы сводится к следующей математической задаче. Пусть в n -мерном пространстве заданы m точек ( m > n ), в которых известны значения функции f . Необходимо построить формулы (1) для приближенного вычисления первых частных производных данной функции. Задача является корректной, если множество точек не принадлежит какой-либо гиперплоскости в Rⁿ . Известны следующие подходы к построению данных формул.

Формулы естественной аппроксимации производных в R² [2; 15]. Пусть задан выпуклый m -угольник (либо невыпуклый, но без самопересечений) в системе координат ( x ¹, x ²). Значения функции заданы в его вершинах. Тогда справедливы следующие формулы, аппроксимирующие её частные производные минимум с первым порядком точности:

k = 1

. (2)

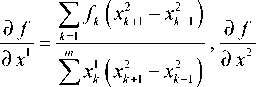
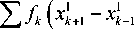
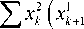
k = 1

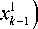
В формулах (2) вершины многоугольника должны быть пронумерованы по порядку по ходу часовой стрелки (или против), верхние индексы – номер координаты, нижние – номер узла конечного элемента. Для нижних индексов действует правило циклической перестановки индексов, т.е. x 0 = x m , x m ₊ ₁ = x 1 .

Аппроксимация производных для элементов в виде симплексов. Отметим, что для симплексов задача ап-

проксимации частных производных с первым порядком точности имеет единственное решение. Данные формулы справедливы для пространств любой размерности. Пусть элемент в n -мерном пространстве содержит m = n + 1 вершин (является симплексом). Тогда n -мерный объем элемента можно записать как det V /( n !) ,

где V – квадратная матрица. В трехмерном случае она имеет вид

V =

или

V =

x ₁	^- x 4	x ₁	^- ^x 4	x ₁	^- x 4
_x 1 ₂	^- x 4	^x 2²	^- x 4	^x 2³	^- x 4
_x 1 ₃	^- x 4	^x 3²	^- x 42	^x 3³	^- ^x 4

(матрицы разные, но их определители равны между собой). Матрица V_j получается из V заменой j -го столбца столбцом col ( f. ^- fm ,..., f_m- 1 ^- ^fm ) ^:

	f\ ^— ^f4. ^x 1 ^— x 4 ^x 1 ^— x 4
V =	^f 2 ^— f 4 x 2 - x 4 x 2 - x 4	^,
	f 3 ^— f 4 x 3 ^— x 4 x 3 ^— x 4
	x 1 ^— x 4 ^f1 ^— f 4 x 1 ^— x 4
V =	x 2 - x 4 ^f 2 - ^f 4 x 2 - x 4	, (4)
	x 3 ^— x 4 ^f 3 ^— f x 3 ^— x 4
	x 1 ^— x 4 x 1 ^— x 4 f1 ^— f 4
V 3 =	x 2 - x 4 x 2 - x 4 ^f 2 - f 4
	x 3 ^— x 4 x 3 ^— x 4 ^f3 ^— f 4

Формула для аппроксимации производных в конечном элементе имеет следующий вид:

det V

— =--- j . (5)

d x j det V

Отсюда следует, что коэффициенты операторов (1) d +, d 2 +, d 3 выражаются через миноры:

в =

.2 .2 .3.3

x 2 - x 4 x 2 - x 4

.2 .2 .3.3

x3 - x4 x3 -

det V

P2 =

2 2

x ₃ - x 4

2 2

x 1 - x 4

det V

- x:

P3 =

x_: - x 4

2 2

x ₂ - x 4

det V

- x

P4 =

-P1 -в -P3

и т.п. Аналогичные формулы для коэффициентов матрицы деформаций линейного 4-узлового элемента приведены в [1]. Для интересующего нас случая 8-узлового конечного элемента рассмотрим подход, позволяющий применить формулы (5). Данный подход естественным образом сформировался при построении ажурной схемы МКЭ [16; 17] и её развития – моментного конечного элемента [18].

Ажурная схема МКЭ

ных элементов. В частности, это высокая экономичность, лучшая сходимость, отсутствие эффектов сдвигового и объемного запирания и неустойчивости типа «песочные часы». В литературе описан факт влияния взаимного расположения конечных элементов на точность численных решений [20]. В [21] исследовано влияние взаимного расположения 4-узловых конечных элементов при различных способах разбиения гексаэд-рических ячеек на 5 или 6 тетраэдрических элементов. Среди них наилучшую сходимость продемонстрировала ажурная схема. Очевидно, что в ажурной схеме для аппроксимации производных используется формула (5).

Моментная схема МКЭ

В развитие идеи ажурных схем в [18] для решения задач теории упругости при m =8 предложен способ использования формулы, аналогичной (5). Для её применения к 8-узловому конечному элементу было предложено рассмотреть правильный симплекс с 8 узлами в 7-мерном пространстве, вписанный в 7-мерный куб. В 7-мерном пространстве рассмотрим симплекс, вписанный в параллелепипед с ребрами h ₁, h ₂, h ₃, h ₄, h ₅, h ₆, h ₇(семимерный аналог конечного элемента ажурной схемы), для которого формула (3) принимает вид:

Формулы (5) справедливы, если конечный элемент является симплексом в n -мерном пространстве и его единственными узлами являются вершины данного симплекса. В [16] предложена ажурная схема МКЭ, когда расчетная область покрывается сеткой из шестигранных ячеек, а расчетные элементы в виде тетраэдров располагаются по одному в центрах данных ячеек (рис. 1). Остальные 4 тетраэдра данного шестигранника в расчетах не участвуют, а их экстенсивные характеристики (объем, масса и другие) присоединяются к внутреннему расчетному элементу.

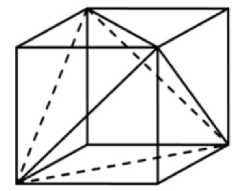
Рис.1. Ячейка ажурной сетки

Fig. 1. The rare mesh cell

Данную схему можно иначе интерпретировать как 4-узловой конечный элемент в виде гексаэдра. Подробное исследование, верификация и валидация данной схемы МКЭ при решении нестационарных трехмерных задач теории упругости и пластичности с использованием явной схемы «крест» [17; 19] показало ее высокое качество и ряд преимуществ по сравнению с традиционными схемами на базе 4-узловых и 8-узловых конеч-

	1	0	0	0	0	0	0	0
	1	0	0	h ₃	0	h ₅	h ₆	h ₇
	1	0	h ₂	0	h ₄	0	h ₆	h ₇
V =	1	0	h ₂	h ₃	h ₄	h ₅	0	0	(7)
	1	h ₁	0	0	h ₄	h ₅	0	h ₇	(7)
	1	h ₁	0	h ₃	h ₄	0	h ₆	0
	1	h ₁	h ₂	0	0	h ₅	h ₆	0
	1	h ₁	h ₂	h ₃	0	0	0	h ₇

При h j = h ₂ = h 3 = h ₄ = h ₅ = h₆ = h 7 = 1 данный симплекс является правильным (все его ребра равны между собой, центр совпадает с центром единичного 7-мерного куба), а набор вершин в трехмерном пространстве (столбцы со второго по четвертый) образует единичный трехмерный куб. Если вершины трехмерного куба заменить на вершины произвольного гексаэдра, формула (7) принимает вид

	1	^x 1 ¹	x 1 ²	^x 1 ³	0	0	0	0
	1	_x 1 ₂	^x 2 ²	^x 2 ³	0	h ₅	h ₆	h ₇
	1	^x 3 ¹	^x 3 ²	^x 3 ³	h ₄	0	h ₆	h ₇
V =	1	_x 1 ₄	x 4 ² x 5 ²	^x 4 ³ ^x 5 ³	h ₄	h ₅	0	0	. (8)
	1	_x 1 ₅	x 4 ² x 5 ²	^x 4 ³ ^x 5 ³	h ₄	h ₅	0	h ₇	. (8)
	1	_x 1 ₆	x 6 ²	^x 6 ³	h ₄	0	h ₆	0
	1	_x 1 ₇	^x 7 ²	^x 7 ³	0	h ₅	h ₆	0
	1	^x 8 ¹	² x ₈	³ x ₈	0	0	0	h ₇

Далее для вычисления производных можно использовать формулу (5), используя вместо (3) формулу (8).

Если использовать производные только по трем фактическим координатам, придем к схеме Уилкинса, недостатком которой является наличие эффекта неустойчивости типа «песочные часы» (мод с нулевой энергией). Для борьбы с данным видом неустойчивости в [18] предлагается использование также и производных по фиктивным координатам x4, x5, x6, x7. Это соответствует учету в конечном элементе моментных составляющих, постоянных в пределах элемента, и исключает моды нулевой энергии типа изгиба и кручения. Шаги сетки h4,h5,h6,h7 при этом превращаются в параметры конечного элемента, с помощью которых можно регулировать учет моментов. В этом случае тензор деформаций в элементе нужно принять в виде

г ij

^11 е12 E13 е14 E15 E16

E21 ^22 e23 e24 e25 ^26

. E31 e32 ^33 e34 e35 e36

e ij

2 ( d i u j + d'u ) ^j ^ 3, = ^

1 ^+

2 du J > 3,

а тензор напряжений соответственно

с.	^ 12	0 13	^О 14	^О 15	^О 16	^О ¹⁷
° 21	^О 22	^О 23	^О 24	^О 25	^О 26	^О 27	. (10)
_° 31	° 32	^О зз	^О 34	^О 35	^О 36	^О 37 _

Элементы последних 4 столбцов матрицы (10) соответствуют некоторым аналогам изгибающих и крутящих моментов конечного элемента. Моментные составляющие напряжений используются в некоторых неклассических моделях сплошных сред [22; 23], но в рассматриваемом случае они не имеют отношения к данным моделям и применяются исключительно для улучшения качества численных методов.

Сделаем замечание о подборе параметров h ₄, h ₅, h ₆, h ₇. При больших значениях данных параметров влияние моментов уменьшается, и схема МКЭ приближается по свойствам к схеме Уилкинса, т.е. может проявляться эффект песочных часов. С другой стороны, при их значениях меньше, чем min( h ₁, h ₂, h ₃), в явных схемах возникают более жесткие ограничения на временной шаг. В нашей практике решения задач теории упругости все данные параметры принимались равными:

h 4 = h 5 = h 6 = h =^ h , (11)

где h – характерный размер конечных элементов решаемой задачи, например, min( h ₁, h ₂, h ₃) . Эмпирически лучшие результаты получались при значениях безразмерного параметра ^ в пределах от 1 до 1,5.

Вырожденные элементы

Отметим еще одну особенность данного подхода. При решении задач могут встречаться и элементы вырожденной формы с числом узлов менее 8. В ANSYS в этих случаях используется 8-узловое кодирование элемента [24], при котором последний фактический узел записывается несколько раз. Так, если в стандартном случае список глобальных номеров узлов элемента имеет вид i ₁, i ₂, i ₃, i ₄, i ₅, i ₆, i ₇, i ₈, то для элемента в виде треугольной призмы – i ₁, i ₂, i ₃, i ₄, i ₅, i ₆, i ₆, i ₆, а для тетраэдра – i ₁, i ₂, i ₃, i ₄, i ₄, i ₄, i ₄, i ₄. Если применить аналогичный прием и ввести в формуле (8) повторяющиеся координаты последнего узла, например, для призмы или тетраэдра

	' 1	^x 1 ¹	^x 1 ²	^x 1 ³	0	0	0	о ’
	1	_x 1 ₂	^x 2 ²	^x 2 ³	0	h ₅	h ₆	h ₇
	1	^x 3 ¹	^x 3 ²	^x 3 ³	h ₄	0	h ₆	h ₇
V =	1	_x 1 ₄	^x 4 ²	^x 4 ³	h ₄	h ₅	0	0
призм	1	^x 5 ¹	^x 5 ²	^x 5 ³	h ₄	h ₅	0	h ₇	’
	1	_x 1 ₆	^x 6 ²	^x 6 ³	h ₄	0	h ₆	0
	1	_x 1 ₆	^x 6 ²	^x 6 ³	0	h ₅	h ₆	0
	1	_x 1 ₆	^x 6 ²	^x 6 ³	0	0	0	h 7	(12)
								-1	(12)
	' 1	x ₁ ¹	x ₁ ²	x ₁ ³	0	0	0	0
	1	x ¹ ₂	x ₂ ²	x ₂ ³	0	h ₅	h ₆	h 7
	¹	x ₃ ¹	x ₃ ²	x ₃ ³	h ₄	0	h ₆	h ⁷
V =	1	x ¹ ₄	x ₄ ²	x ₄ ³	h ₄	h ₅	0	0
тетр	1	x ¹ ₄	x ₄ ²	x ₄ ³	h ₄	h ₅	0	h	^,
	1	x ¹ 4	x 4 ²	x 4 ³	h ₄	0	h ₆	0
	1	x ¹ ₄	x ₄ ²	x ₄ ³	0	h ₅	h ₆	0
	1	x ¹ ₄	x ₄ ²	x ₄ ³	0	0	0	h 7 _

то формула (5) сохраняет свою применимость, поскольку определитель матрицы (8) (в частности, определители (12)) будет отличен от нуля для любого элемента ненулевого трехмерного объема. Таким образом, данный подход остается работоспособным и для элементов вырожденной формы.

Численные результаты

Описанное выше проиллюстрируем результатами решения модельных статических задач теории упругости с использованием моментного конечного элемента [18]. Результаты решения некоторых статических задач приведены в [18]. Здесь приведем результаты, иллюстрирующие работу с вырожденными элементами и неустойчивостью типа «песочные часы».

Изгиб бруса квадратного сечения

Рассматривается геометрически и физически линейная задача об изгибе бруса квадратного сечения под действием распределенной нагрузки.

Брус длиной L =10 см квадратного сечения H 1 = H 2 = 1 см (рис. 2) защемлен на торцах. Давление p = 10 МПа равномерно распределено на участке поверхности 4 < x < 6 . Механические свойства материала: р = 7,8 г/см 3 , E = 210 ГПа, коэффициент Пуассона V = 0,3.

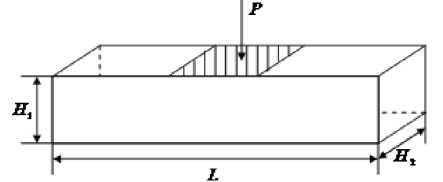
Рис. 2. Брус квадратного сечения давление. Свойства материала: р = 7,8 г/см3, E = 210 ГПа, коэффициент Пуассона V = 0,3. Граничные условия: жесткое закрепление контуру диска, на одной свободной поверхности задавалось давление p = 17 МПа. Данная осесимметричная задача решалась как трехмерная. Расчетная область (четверть диска) в первом случае покрывалась кусочно-регулярной сеткой из трех блоков в виде топологических параллелепипедов. Задача решалась на сетке 28 ячеек вдоль радиуса и 6 ячеек по толщине диска. Каждый из блоков покрывался сеткой 14x14 четырехугольных ячеек в плане. По толщине диска сетка равномерная. Во втором случае использовалась равномерная сетка из прямоугольных параллелепипедов (в плане – квадраты со стороной R /28, размер по толщине – H /6). Вблизи криволинейной границы имелись вырожденные ячейки в виде гексаэдров неправильной формы или треугольных призм. На рис. 4 приведено сравнение решений на двух сетках – зависимость прогибов диска от полярной координаты r.

Fig. 2. A square beam

Использовалась равномерная сетка 4×4×40 ячеек в форме куба со стороной h 1 = h 2 = h ₃ = 0,25. В первом варианте каждый 8-узловой элемент совпадал с ячейкой. Во втором варианте каждая ячейка разбивалась на две равных треугольных призмы. В третьем варианте каждая ячейка разбивалась на 6 конечных элементов в виде тетраэдра. На рис. 3 приведены графики прогибов на оси стержня. Значения параметров моментной схемы принимались равными: h 4 = h ₅ = h₆ = h 7 = 1,4 h 1 .

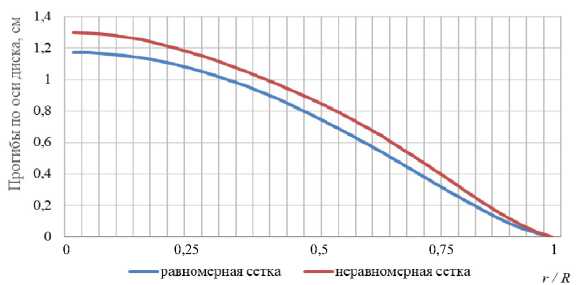
Рис. 4. Сравнение решений на неравномерной сетке из гексаэдров и равномерной сетке с вырожденными элементами

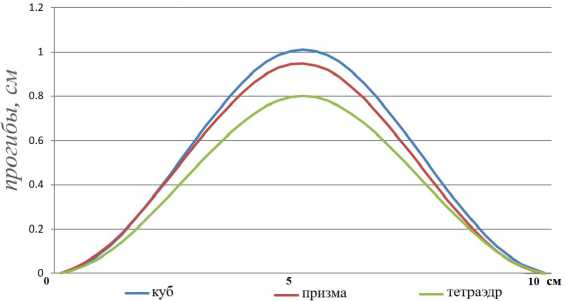
Рис. 3. Прогибы на оси бруса

Fig. 3. Deflections on the beam axis

Отметим, что сходимость схем на базе призм и тетраэдров более медленная в связи с наличием эффекта сдвигового запирания.

Деформирование диска под действием внешнего давления

К круглому диску радиуса R = 14,85 см толщиной H = 1,5 см, закрепленному по контуру, приложено постоянное равномерно распределенное по поверхности

Fig. 4. Comparison of solutions on a non-uniform mesh of hexahedrons and a uniform mesh with degenerate elements

Приведенные решения двух задач показывают работоспособность данного конечного элемента при использовании вырожденных ячеек

Влияние параметров моментной схемы на «песочные часы»

На примере той же задачи с диском продемонстрируем влияние параметров моментной схемы на эффект неустойчивости «песочные часы» (результаты из работы[18]).

Использовалась неравномерная сетка из гексаэдров, описанная выше . Задача решалась с использованием моментной схемы с двумя разными значениями регулируемых параметров. Как и в первой задаче, воспользуемся безразмерным параметром. Поскольку сетка неравномерная, за основу возьмем размеры ячейки в центре пластины, по форме близкую к прямоугольному параллелепипеду: h 1 = h ₂ ~ 0,5, h ₃ = 0,25 . Параметры схемы принимались в виде h 4 = h ₅ = h ₆ = h 7 = ^ h ₃ при значениях параметра ^ = 1 и ^ = 40. На рис. 5 представлен вид четверти деформированного диска при ξ = 1:

Fig. 5. A deformed part (ξ = 1)

Рис. 6. Деформированный диск (ξ = 40)

Fig. 6. A deformed part (ξ = 40)

На рис. 6 - тот же вид при ^ = 40 . На обоих рисунках перемещения увеличены в 20 раз.

Решение на последнем рисунке имеет значительные нефизические искажения, обусловленные неустойчивостью «песочные часы».

Заключение

Рассмотрен новый способ аппроксимации производных в 8-узловых конечных элементах. Применение данного подхода позволяет строить эффективные численные схемы МКЭ, свободные от недостатков типа неустойчивости «песочные часы» и сдвигового запирания. Поскольку в работе рассматривался фактически только геометрический аспект построения численных схем, все другие вопросы, такие как геометрическая и физическая нелинейность и т.п., могут быть решены известными методами без всяких ограничений. Данный подход может быть применен к решению широкого класса задач математической физики, в частности, для более сложных моделей в механике деформируемого твердого тела [25] и электромагнетизма [26].

Список литературы Об одном способе аппроксимации производных в гексаэдрических 8-узловых конечных элементах

Зенкевич, О. Метод конечных элементов в технике / О. Зенкевич. – М.: Мир, 1975. – 541 с.
Уилкинс, М.Л. Расчет упругопластических течений / М.Л. Уилкинс // Вычислительные методы в гидродинамике. – М.: Мир, – 1967. – С. 212–263.
Голованов, А.И. Метод конечных элементов в механике деформируемых твердых тел / А.И. Голованов, Д.В. Бережной. – Казань: Дас, 2001. – 300 с.
Ohya, Y. FEM model of Biot’s equations free from volume locking and hourglass instability / Y. Ohya, N. Youshida // The 14th World Conference on Earthquake Engineering. October 12-17. – 2008. – Beijing, China.
Sun, E.Q. Shear locking and hourglassing in MSC, Nastran, ABAQUS, and ANSYS / E.Q. Sun // MSC Software Users Meeting, – 2006.
Красновский, Е.Е. Точность решения задач механики в ANSYS при наличии изгибных напряжений / Е.Е. Красновский, А.С. Шадский // Вестник Московского государственного технического университета им. Н.Э. Баумана. Серия «Естественные науки». – 2011. – С. 169–175.
de Souza Neto, E. F-bar-based linear triangles and tetrahedral for finite strain analysis of nearly incompressible solids. Part I: formulation and benchmarking / E. de Souza Neto, F.M.A. Pires, D.R.J. Owen // Int. J. Num. Methods Engng. – 2005. – Vol. 62, iss. 3. – P. 353–383. DOI: 10.1002/nme.1187
Luo, Yunhua. On Shear Locking in Finite Elements / Luo Yunhua // Department of Structural Engineering. Royal Institute of Technology. S-100 44 Stockholm, Sweden. – TRITABKN. Bulletin 29. – 1997. – 120 p.
Overcoming volumetric locking in material point methods / W.M. Coombs, T.J. Charlton, M. Cortis, Ch.E. Augarde // Computer Methods in Applied Mechanics and Engineering. – 2018. – Vol. 333. – P. 1–21.
Yuvakishore, Bh. Shear locking reduction in family of plane quadrilateral elements / Bh. Yuvakishore, R. Yogeshwaran, P.V. Jeyakathikeyan // IOP Conf. Series: Materials Science and Engineering 402. – 2018. – 012074. DOI: 10.1088/1757-899X/402/1/012074
Xiaoshan, L. Nonlinear Finite Element Analysis of Composite and Reinforced Concrete Beams / L. Xiaoshan, Y.X. Zhang, P. Prabin // Woodhead Publishing Series in Civil and Structural Engineering, – 2020. – P. 9–27.
Telikicherla, R.M. Treatment of near-incompressibility and volumetric locking in higher order material point methods / R.M. Telikicherla, G. Moutsanidis // Computer Methods in Applied Mechanics and Engineering. – 2022. – Vol. 395. – 114985. DOI: 10.1016/j.cma.2022.114985
Bieber, S. Locking and Hourglassing in Nonlinear Finite Element / S. Bieber // Technology Bericht Nr. 76. Institut fir Baustatik und Baudynamik der Universitat Stuttgart, – 2024. – 183 p.
Reese, S. A stabilization technique to avoid hourglassing in finite elasticity / S. Reese, P. Wriggers // Internat. J. Numer. Methods Engrg. – 2000. – Vol. 48, iss. 1. – P. 79–109. DOI: 10.1002/(SICI)1097-0207(20000510)48:1<79::AID-NME869-3.0.CO;2-D
Reddick, H.W. Advanced Mathematics for Engineers / H.W. Reddick, F.H. Miller. – 3rd ed. – Wiley. New York, 1955. – 548 p.
Ажурная схема численного решения трехмерных динамических задач теории упругости и пластичности / А.В. Жидков, С.В. Зефиров, К.А. Кастальская, С.В. Cпирин, Д.Т. Чекмарев // Вестник ННГУ. – Н. Новгород: Изд-во ННГУ, 2011. – № 4, Ч. 4. – С. 1480–1482.
Крутова, К.А. Численное решение трехмерных динамических задач теории упругости и пластичности на основе ажурной вариационно-разностной схемы: дис.... канд. физ.-мат. наук; Нижегородский гос. университет / К.А. Крутова. – Нижний Новгород, 2015.
Абу Даввас, Я. Моментный конечный элемент для решения трехмерных задач теории упругости / Я. Абу Даввас, И.А. Модин, Д.Т. Чекмарев // Проблемы прочности и пластичности: межвуз. сб.; Нижегородский ун-т. – 2023. – Т. 85, № 2. – С. 164–177. DOI: 10.32326/1814-9146-2022-85-2-164-177
Численное решение трехмерных динамических упругопластических задач с использованием ажурной схемы метода конечных элементов / А.В. Жидков, К.А. Крутова, А.А. Миронов, Д.Т. Чекмарев // Проблемы прочности и пластичности. – 2017. – Т. 79, № 3. – С. 327–337. DOI: 10.32326/1814-9146-2017-79-3-327-337
Горельский, В.А. Исследование влияния дискретизации при расчете методом конечных элементов трехмерных задач высокоскоростного удара / В.А. Горельский, С.А. Зелепугин, А.Ю. Смолин // Журнал вычислительной математики и математической физики. – 1997. – Т. 37, № 6. – С. 742–750.
Крутова, К.А. О влиянии взаимного расположения конечных элементов на точность численного решения задач теории упругости / К.А. Крутова, С.В. Спирин, Д.Т. Чекмарев // Проблемы прочности и пластичности: межвуз. сб.; Нижегородский ун-т. – 2013. – Вып. 75. – № 4. – С. 312–322.
Romanov, A.V. Application of the Reduced and Selected Integration Method in Problems of Micropolar Elasticity Theory / A.V. Romanov // Moscow University Mechanics Bulletin.
Прозорова, Э.В. Влияние момента на структуры сплошной среды при взаимодействии газа и жидкости с поверхностью / Э.В. Прозорова // Материалы XV Международной конференции по прикладной математике и механике в аэрокосмической отрасли (AMMAI’2024), 1–8 сентября, Алушта. – 2024. – С. 171–173.
Басов, К.А. ANSYS для конструкторов / К.А. Басов. – М.: ДМК Пресс, 2009.
Горохов, В.А. Верификация программных средств конечно-элементного моделирования упругопластического деформирования элементов конструкций при квазистатических, циклических и терморадиационных нагружениях / В.А. Горохов // Материалы XV Международной конференции по прикладной математике и механике в аэрокосмической отрасли (AMMAI’2024), 1–8 сентября, Алушта. – 2024. – С. 135–136.
Калинин, А.В. Пространства вектор-функций и стационарные задачи электромагнитной теории: учеб. пособие / А.В. Калинин, А.А. Тюхтина. – Нижний Новгород: Нижегородский госуниверситет, 2021. – 112 с.

Еще

Статья научная