Об одном способе поиска оптимального управления в неоднородной дискретной системе с запаздыванием по состоянию процессов

Изучение процессов с запаздыванием имеет долгую историю. Первым на необходимость учета предшествующего состояния системы для ее полного описания, качественного исследования и прогнозирования поведения обратил внимание Вольтера [1] при анализе математических моделей численности биологических популяций. Позднее на этот же факт указали специалисты по технологиям и управлению в таких сферах как экономика, экология, диагностика технических устройств, химико-технологические процессы, передача информации, ядерные процессы, космонавтика и многих других. Отметим лишь некоторые из этих работ [3 , 4 , 10] .Традиционно поиски решения для задач оптимального управления в системах с запаздыванием начались с моделей, описываемых дифференциальными уравнениями. Позднее состоялось обращение к дискретным системам. Во всех этих случаях исследования были связаны с получением условий типа принципа максимума Понтрягина, перечислить все работы такого плана не представляется возможным. Примерами могут служить работы [13, 14] . В данной работе сделана попытка получения достаточных условий оптимальности типа Кротова для неоднородных дискретных систем (НДС) с промежуточными критериями, содержащих два уровня. Системы нижнего уровня включают в себя переменные состояния с запаздыванием. Найденные условия используются для построения метода улучшения первого порядка и формулирования его алгоритма. Алгоритм апробирован на иллюстративном примере.

1.    Неоднородные дискретные процессы с запаздыванием по состоянию и промежуточными критериями

Будем рассматривать двухуровневую модель, в которой нижний уровень представлен дискретными динамическими системами однородной структуры с запаздыванием по соответствующему состоянию. На верхнем уровне действует дискретная модель общего вида

• (1)               x(k + 1) = f (k,x(k'),u(k')'),

k G K = {kI,kI + 1,...,kF}, u G U(k,x), где k— номер шага, kI, kF — соответственно начальный и конечные шаги; x и u— соответственно переменные состояния и управления произвольной природы (возможно различной) для различных k; U(k,x) — заданное при каждом k и x множество.

Выделено подмножество K‘ С K, kF G К’, на котором u(k) предстает в виде пары (uv(k),md(k)), где uv — управление верхнего уровня, а md(k) — дискретный процесс (xd(k,t),ud(k,t)), t G T(k, z(k)), md(k) G Dd(k, z(k)). Под Dd понимается множество допустимых процессов md, удовлетворяющих системе xd(k, t + 1) = fd(k, z, t, xd(k, t), xd(k, t — тk),ud(k, t)),

• (2)                t G T = {t i (z),t i (z) + 1,...t F (z)},

x d (k,t) = e(k,t), tI (z).

xd G Xd(k,z,t), ud G Ud(k, z,t, xd), z = (k,x,uv), t — номер шага, ti (z), tF (z) — соответственно начальный и конечный шаги при каждом k, e(k,t) — заданные функции. Для системы (2) на множестве T задана промежуточная цель в виде функционала, который необходимо минимизировать:

I ^k =   ^^    f ^k (t,x ^d (k,t),x ^d (k,t — т ^k ),u ^d (k,t)) ^ inf .

T( z ) \ t F ( z )

Здесь X ^d (k, z,t), U ^d (k, z, t, x d ) — заданные при каждом t, z и x ^d множества.

Оператор правой части (1) на множестве K ^′ сводится к следующему:

f (k,x,u) = d(z,Y ^d (z)), где Y d = (t i ,xj,t F ,x dF ,y j ,y F ) G r ^d (k,z), r ^d (z) = {Y d : t I = т(k, z),t _F = ^(k, z),x I = ^(k, z),x F G r F (k, z)}.

На множестве D процессов m = (x(k), u(k), xd(k,t),xd(k,t — тk),ud(k,t)), удовлетворяющих (1), (2), рассматривается задача оптимального управления о минимизации терминального функционала I = F(x(kF)) при фиксированных ki = 0, kF, x(ki) и дополнительных ограничениях x(k) G X(k). Подчеркнем, что на каждом дискретном шаге k G К’ модель рассматривает дискретный процесс m(k), управление которым состоит из фиксированной на шаге дискретной части u и дискретно изменяемой части md.

Замечание 1. Уравнение типа (2) нетрудно преобразовать к уравнению вида (1) . Пусть x(t + 1) = f (t, x(t), x(t — q), u(t)), q >  1. Положим y 1 (t) = x(t — 1), y ² (t) = x(t — 2), .. .,y ^q (t) = x(t — q). Тогда y 1 (t + 1) = x(t) y ² (t + 1) = y 1 (t), .. ., y ^q (t + 1) = y ^{q - 1} (t). Окончательно имеем следующую систему типа (1) : x(t + 1) = f (t, x(t),y 1 (t),y²(t, .. ., y q (t)),u(t)), y 1 (t + 1) = x(t), y ² (t + 1) = y 1 (t), .. ., y q (t + 1) = y ^{q - 1} (t).

2.    Достаточные условия оптимальности

За основу для получения достаточных условий оптимальности взят принцип расширения [7] .

Прежде чем получить указанные условия для рассматриваемой задачи введем в рассмотрение новые переменные xok и преобразуем подзадачу нижнего уровня к виду:

xd(k, t + 1) = f d(k, z, t, xd(k, t),ud(k, t),yT(k, t)), xok(k, t + 1) = xok(k, t) + fk(t, xd(k, t), ud(k, t),yT(k, t)),   x0(tI(z)) = 0,

Ik = x^Ok

x ^d = (x ^d ,x ⁰ ), f ^d = (f ^d ,f ^k ).

Далее вводится множество E процессов m , в котором исключены дискретные цепочки, и обобщенный лагранжиан по аналогии с лагранжианом для НДС [12] :

L = G(x(k F )) — ^ R(k,x(k'),u(k')')+

K \ K ^′ \ k F

+ ^(G ^d (z) - ^ R d (z,t,x ^d (k,t),u ^d (k,t),y ^T (k,t))y K ‘             T (z) \ t F

G(x) = F(x(k F )) + ф(k F , x) — ф^,x(k i )),

R(k, x,u) = ф (k + 1, f (k, x, u)) — ф (k, x) ,

G ^d (k, z, Y d ) = —ф(k + 1, d(k, z, Y d )) + ф(k, x(k)) — x ^0k (k, t F )+

+ ф^, z, t F , x ^dF , y F ) — ф^, z, t i ,x I , y^),

R ^d (k, z, t, x^d, u ^d ,y ^T ) = ф ^d (k, z,t +1, f ^d (k, z, t, x ^d , u ^d , y ^T )) —

— f k(t, xd, ud, yT) — ^>d(k, z, t, xd, yT), ^d(k,z,t)=      sup      Rd(k,z,t,xd,yT ,ud), xdexd(k,z,t),yT exd ud G Ud(k, z, t, xd), ld(k,z)=         inf         Gd(k,z,Yd),

Y d ^ r d ( k,z ) ,x ^d E X d ( k,z,t f )

{ sup       R(k,x,u), t G K \ K ‘ ,

M^{( k )}

l

x E X( k ) ,u E U( k,x )

—nf        ld(z),       k G K‘, xGX(k),uv eUv(k,x)

inf    G(x).

x e r n x( k F )

Здесь ф(k,x) — произвольный функционал, ф^к, z,t,x d ,y^T,x ^0k ) = ф ^d (k,z,t,x ^d ,y^T ) — x ^0k — произвольное параметрическое семейство функционалов (с параметрами k , z ).

Легко убедиться, что L(m) = I(m) при m G D , т. е. при выполнении отброшенных связей L(m) совпадает с I(m). Действительно, при m G D , как видно,

R = ф(к + 1, x(k + 1)) — ф(к, x),

R d = ф ^d (k, z,t + 1,x ^d (t + 1)) —

• —    f k (t,x d (k,t),u d (k,t),y^T(k,t) - ф ^d (k,z,t,x ^d ,y^т),

G ^d (k, z, Y d ) = —ф(k + 1,9(k, z, y d )) + ф(k, x(k))+

• +    ф ^d (k, z, t F , x ^dF , y ^T ) — ф ^d (k, z, t i ,x d y ^T ),

L = F(x(k F )) + ^ (ф(k,x') — ф(k,x)) +

K \ K ‘

• +    ^( ^ {ф ^d (k,z,t,x ^d y ^т ) — ф^d(k,z,t,x^dy ^т ))^. K ‘ T (k,z)

Отсюда непосредственно следуют теоремы, аналогичные теоремам для НДС [12] .

Теорема 1. Пусть даны последовательность процессов { m _s } ⊂ D и функционалы φ , φ ^d , такие что:

• (1 )    R(k,x s (k'),u s (k')') ^ ^(k'), k G K ;

• (2)    R^d(-z s ,t, x d (t),u d (t),y S ) — ^ ^d (z s ,t) ^ 0, k G K ‘ ,t G T (z s ) ;

• (3)    G ^d (z s ,Y d ) — l ^d (z s ) ^ 0, k G K ‘ ;

• ⁽ 4 )    G ⁽ x s ^(t F )) ^ l .

Тогда последовательность { m _s } — минимизирующая для I на D .

Теорема 2. Для любого элемента m ∈ D и любых функционалов φ , φ ^d имеет место оценка

I(m) — inf I <  A = I(m) — l.

Пусть имеются два процесса m ¹ G D и m ¹¹ G E и функционалы ф и ф ^d такие, что L (m ¹¹) < L (m¹) = I (m¹) и m ¹¹ G D . Тогда I (m ¹¹ ) < I(m ¹ ) .

Рассмотрим теперь доказательство этих теорем.

Итак, утверждение теоремы 2 становится очевидным поскольку элементы m ¹ G D , m ¹¹ G D , а на этом множестве функционалы L и I совпадают.

Далее из определения l, l ^d , µ, µ ^d следует, что для любых m ∈ D I = L ⩾ l . В силу условий 1)-4) существует последовательность { m _s } , на которой предел L = I равен l. Отсюда следует утверждение теоремы 1.

3.    Метод улучшения управления

Предположим, что X (k) = R ^m(k) , X d (z,t) = R ^n(k) , x d = ^(z), k _I , x _I , k F , t i (k) t F (k) e(k,t) — заданы, x F G R ^n(k) и системы нижнего уровня не зависят от управления u ^v .

Основу для построения метода составляют задача улучшения и принцип расширения [2, 7] . Задача улучшения состоит в построении некоторого оператора n(m), П ^: D ^ D ,обладающего свойством I(n(m)) С I(m). Если задан начальный элемент, то оператор генерирует улучшающую, в частности, минимизирующую последовательность {m s } : m s+i = n(m s ).

Согласно указанному принципу расширения по заданному элементу m ^I G D требуется найти элемент m ^II G D , на котором I (m ^II ) = L(m ^II ) <  I (m ¹ ) = L(m ). Иначе L(mⁿ) — L(m ^I ) <  0. Рассмотрим приращение функционала L(m), которое представим в виде

AL « G T A x f — x

£  (TAu +|au^tR_mmAu) +

K \ K ‘ \kF '                                      '

+ £ ^G dT Ax F + G d ^T Ax) + K ‘ \ k _F

+ £ (G X ^{T A x} F + G X ^{T A x} + ^G d ^{T A}y F ) - K ‘ \ k F

— £ (r^ T Ax d + R d ^T Ax + R^ Ay + R d T Au d + 1-Au ^dT R u u Aud} ,

T(z)\tF где Au = u — u1, Ax = x—x1, Aud = ud — udI, Axd = xd — xdI, AyT = yT — yTI, AxF = xF — xF1, xf = x(kF). Здесь производные функций R, G, Rd, Gd подсчитаны при u = uI(k), x = xI(k), xd = xdI(k,t), yTI(k), ud = udI(k,t).

Предположим, что матрицы R _uu и R ^d _{u d u d} отрицательно определены. Найдем Au, Au d доставляющие максимум выражениям, стоящим под знаками сумм        ,       соответственно. Нетрудно видеть, что

K \ K ‘ \ k F T (z) \ t F

Au = —(R uuT' R u ,

△ u ^d = - (R U d u d ) ^{- 1} R U d .

Зададим функции φ, φ ^d в виде:

Ф = ^T (k)x(k), фd = XT (k, t)x(k) + ^dT(k, t)xd(k, t) + qT (k, t)yT(k, t), где ψ, ψd, λ, q— вектор-функции, и таким образом, чтобы приращение функционала AL не зависело от Ax, Axf, Axd, AyT, AxF. Последнее требование будет достигнуто, если:

R x =0, R d = 0, R^d d d = 0, R^d T = 0,

G x = 0, G X = 0, G d d = 0, G^ = 0.

Расшифровка указанных условий приводит к задаче Коши для НДС относительно ψ , ψ ^d , q, λ с начальными условиями на правом конце:

^(k F ) = —F x , ^(k) = H x , k G K \ K ‘ \ k F ,

^(k) = H x + gH_xd + £t^d (k, t i ) + X(t i ) - X(t F ), k G K ‘ ,

^d = H d(k,t)xd , t = ti + T + 1,..., tF — 1, ^d (k,tF) = HxdF ,

X(k,t) = X(k,t +1) + Hx, X(k,tF) = 0, где

H = ^ ^T (k +1) f (k, x(k),u(k)), k G K \ K ‘ \ k F

и

q(k, t) = H d , q(k, t F ) = —0^

H = / T d(k,Y ^d ), k G K ‘ ,

H ^d = ^ ^dT (k, t + 1)f ^d (k, t, x(k),x ^d , y ^T (k),u^d) — f ^k (t, x ^d , y ^T (k),u ^d ), x(k i )= X i , x(k F )= X F , x ^d (k,t i )= x d , X ^d (k,t F )= x F , y ^T (k,t i )= y I , y ^T (k,t F )= y F .

При этом

△ u(k = —H^H u ,

△ u^d(k,t) = —(H U d u d ) ^{- 1} H d d .

Следует отметить, что ^ ^dT (k,t) = 0, t > t F (k). Это утверждение может быть получено по аналогии с обычными дискретными процессами с запаздыванием как и в [14] .

4.    Итерационная процедура

На основе полученных соотношений можно сформулировать следующую итерационную процедуру.

• 1.    «Слева направо» просчитывается НДС (1), (2) при u = us(k), ud = ud(k,t) и заданных начальных условиях, получается соответствующие траектории (xs(k), xd(k,t)).

• 2.    «Справа налево» разрешается НДС относительно ^(k), ^^d(k,t), q(k,t), A(k,t).

• 3.    Находятся Au, Aud и новые управления u = us(k) + Au, ud = ud(k, t) + Aud.

• 4.    При найденных управлениях и начальном условии x(ki) = xi просчитывается «слева направо» исходная НДС (1), (2). Тем самым определяется новый элемент m_s+1 .

5.    Пример

Процесс итераций заканчивается, когда | I s+1 — I s | ~ 0 с заданной точностью.

Проиллюстрируем работу метода на примере. Пусть задана НДС, состоящая из двух этапов. Первый этап:

xd(t + 1) = —2xd(t) + (ud — 1)2 + xd(t — 2), xd(0) = 1, t = 0,1, 2, 3, 4, 5, т = 2, yT = xd(t — 2), i0 = |(xd(t))2 + 1(ud)3.

Второй этап:

x d (t + 1) = (t — u d ) ² — x^d(t — 1), t = 6, 7, 8,

1 1 = 2(x d ) 2 + u d ,

T = 1, y ^T = x ^d (t — 1),

I = x ^d (9) ^ min .

Здесь I ⁰ , I ¹ — соответственно промежуточные функционалы первого и второго этапов.

Нетрудно видеть, что K = 0,1,2. Поскольку роль связующей переменной на двух рассматриваемых этапах играет xd , то в терминах этой переменной легко записать процесс верхнего уровня:

x(0) = x d (0,0), x(1) = x d (0, 5), x(2) = x d (1, 9), x d (1,6) = x(1).

Тогда в = x d (0, 5), £ = x(1), I = x(2).

Поскольку на обоих этапах процесс нижнего уровня не зависит от переменных состояния верхнего уровня, то А(0, t) = А(1, t) = 0.

Имеем:

f(2) = - 1, f(1) = f(2) + ^ d (1,4),

H d (0, t) = f d (0, t + 1)( - 2x d (t) + (u d - 1) 2 + y ^T ) - ¹(x d (t)) ² - 1(^) 3 , 2            3

Hd(1,t) = f d(1, t + 1)((t - ud)2 - yT) - |(xd)2 - ud, fd(0, t) = -2^d(0, t + 1) - xd, q(0, t) = f d(0, t + т + 1), fd(0, 5) = ^(2), fd(1,t) = -xd, q(1,t) = -fd (1,t + т + 1), fd(1,10) = 0,

H d d (0, t) = 2f d (0, t + 1)(u d - 1) - (u d ) ² ,

H U d u d (0,t) = 2(f ^d (0,t +1) - u d ),

H d d (1,t) = - 2f ^d (1,t + 1)(t - u d ) - 1, H d d u d (М = ²^(М +¹).

Были проведены вычислительные эксперименты. В начале велся поиск решения примера при различных начальных управляющих воздействиях и одинаковой предыстории. Для расчетов потребовалось 5 итераций. Изменение функционала в обоих случаях представлено в таблице 1, из которой следует, что решения совпадают.

Таблица 1. Результаты расчетов примера 1

Итерация	I = x d (9) ч min
	При начальном u d 2	≡ 1	При начальном u d 2 — 0 . 5
0	9		13
1	-14.637		-14.638
2	-14.658		-14.648
3	-14.699		-14.681
4	-14.914		-14.916
5	-14.915		-14.918

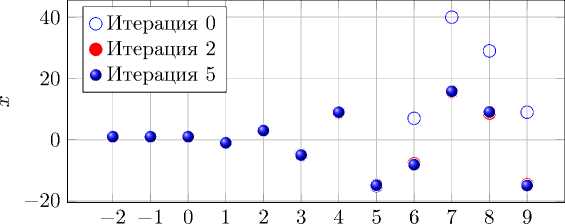
Графики переменных состояния и управления даны на рисунках 1, 2 .

t

Рисунок 1. Состояние. Пример при начальном u ^d,₂ = 1

Итерация 0

Итерация 2

Итерация 5

в в 8

t

Рисунок 2. Управление. Пример при начальном u d_j2 = 1

Далее был осуществлен поиск решения при одном и том же начальном управлении, но с двумя разными предысториями. Результаты представлены в таблице 2 и на рисунках 3, 4 .

Таблица 2. Результаты расчетов примера

Итерация	I = x d (9) ^ min
	Предыстория 1 , 1 , 1	Предыстория — 1 , 0 , 1
0	9	-8
1	-14.637	-31.743
2	-14.658	-31.864
3	-14.699	-31.871
4	-14.914	-31.876
5	-14.915	-31.877

Из полученных результатов видно, что предыстория оказывает

t

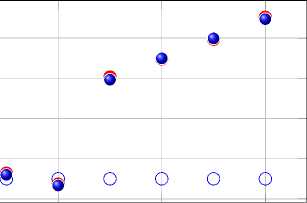
Рисунок 3. Состояние. Пример

Итерация 0

Итерация 2

Итерация 5

- 20

- 2 - 1 0   1   2   3   4   5   6   7   8   9

t

Рисунок 4. Управление. Пример существенное влияние на конечный результат: минимальные значения функционала резко отличаются, тоже происходит с управляющими воздействиями и состояниям процесса.

Кроме того, были выполнены расчеты еще для двух вариантов предысторий. Во всех случаях наблюдается существенная зависимость конечного результата от предыстории. Представление об этом дает таблица 3.

Таблица 3. Рассчитанные значения управления I = x d (9) ^ min

Предыстория	1, 1, 1	-1, 0, 1	2, 1.5, 1	5, 2, 1	-3, 0, 1
Начальное	9.000	-8.000	17.500	50.000	-32
Конечное	-14.915	-31.877	-8.254	24.841	-55.846

6.    Заключение

Таким образом, в работе рассмотрены НДС с промежуточными критериями и запаздыванием по состоянию систем нижнего уровня. Получен аналог достаточных условий оптимальности Кротова, на основе которого построен метод улучшения управления, сформулирован его алгоритм. Предлагаемый метод проиллюстрирован примером, подтверждающим его работоспособность. Расчеты на иллюстративном примере подтвердили многочисленные рекомендации из разных областей науки о влиянии предыстории на развитие модели.