Об одном способе построения начального допустимого базиса в задачах оптимизации

Введение. Пусть система ограничений исходной задачи оптимизации представлена в форме

A x = b ;                                        (1)

a <  x <  в .                                   (2)

Здесь A — матрица размером m x n ( m < n ); a , x , в E R ⁿ ; b E R ^m . Если в исходной задаче среди условий (1) имеются ограничения типа неравенств, то, введя дополнительные неотрицательные переменные, такие ограничения можно преобразовать к равенствам. В расширенной таким образом матрице A дополнительным переменным соответствуют единичные орты (с тем или иным знаком) пространства R ^m . Исходная задача может содержать неограниченные (свободные) переменные x j , что соответствует равенствам a j = —то , в з = + то • Наличие таких переменных упрощает построение начального допустимого базиса.

Для построения начального допустимого базиса существует ряд методов. Во многих коммерческих пакетах (см. [1]) в фазе I (фазе поиска начального базиса) решается следующая m вспомогательная задача линейного программирования: минимизировать   xn+j при усло- j=1

виях aTx ± xn+i = bi, i = 1, 2,...,m, a < x < в, xn+i > 0, i = 1, 2,...,m.         (3)

Здесь a _i ^T — i -я строка матрицы A .

Работа рекомендована к публикации Программным комитетом VIII Международной азиатской школы-семинара “Проблемы оптимизации сложных систем”.

Знак в ограничениях (3) определяется следующим образом. В точке x с координатами

{ai, если ai > —го, ei, если ai = —го, Pi < + го,                           (4)

0 в остальных случаях вычисляется вектор b = b — AX. Если для некоторых i bi < 0, то в i-м ограничении (3) должен быть знак “минус”, в противном случае — знак “плюс”. Это позволяет выбрать в качестве начальной допустимой точки x Е Rn+m вспомогательной задачи точку с координатами xi = xi (i = 1, 2,..., n); xn+i = |bi| (i = 1, 2,..., m), в качестве начальной базисной матрицы — диагональную матрицу размером m х m с элементами ± 1 на диагонали.

Очевидно, что если допустимое множество исходной задачи не пусто, то в оптималь-m ном решении вспомогательной задачи ^ xn+j = 0 и ее оптимальный базис может служить j=1

начальным для фазы II (фазы решения исходной задачи).

Все модификации данного метода сводятся к попыткам уменьшить число искусственных переменных x n ₊ i путем включения в начальный базис фазы I дополнительных или структурных переменных, на которые накладывается требование допустимости их значений. Будем считать, что дополнительная переменная x j имеет границы допустимости a j = 0 , P j = -го , а искусственная — a j = e j = 0.

Алгоритм. В настоящей работе предлагается способ построения начального допустимого базиса, позволяющий использовать на начальном этапе фазы I большее количество структурных и дополнительных переменных, уделяя основное внимание численной сбалансированности начальной базисной матрицы. Из всего набора столбцов матрицы A выбираем (если это возможно) m линейно независимых столбцов и формируем из них базисную матрицу B . Если это не удается сделать, то недостающую часть дополняем единичной подматрицей с соответствующим набором искусственных переменных. Проблема построения начальной базисной матрицы B рассматривается ниже.

Столбцы матрицы A , не вошедшие в матрицу B , объединим в матрицу небазисных столбцов N . Любому небазисному столбцу a j соответствует переменная x _Nj , значение которой всегда равно одному из ее граничных значений ( x Nj = a N или x Nj = e Nj )• Далее каждой небазисной переменной x Nj каким-либо образом (например, по правилу, заданному в (4)) присваивается значение x _Nj . Тогда, если все значения базисных переменных x B = B ¹ ( b — N X N ) имеют допустимые значения, построение начального допустимого базиса заканчивается. В противном случае переопределим значения базисных переменных следующим образом: если x Bi < a Bi , то x Bi = a Bi ; если a Bi <  x Bi <  в Bi , то x Bi = x Bi ; если x Bi > e Bi , то x Bi = e Bi . Здесь a _B , e B Е R m — векторы, составленные из компонент векторов а , в , которые (компоненты) соответствуют базисным переменным.

Пусть r = x _B — X _B и b 0 = Br , тогда верно равенство B X _B + N X N + b 0 = b . Поставим в соответствие столбцу b 0 искусственную переменную x n ₊₁ и запишем систему ограничений (1) в виде системы

Bxb + Nxn + b 0xn+i = b, решением которой является точка XT = (XB, XNN ,xn+1) при xn+1 = 1. Допустимое значение переменной xn+1 есть только нулевое значение, поэтому на следующем этапе устраним недопустимость переменной xn+1, используя точку xо в качестве начальной.

Если столбец b0 плохо масштабирован по сравнению со столбцами матрицы A, например если ||b0||^ < min ||ai||^ или ||b0||^ > max ||ai||^(ai — столбец матрицы A), то можно нормировать вектор b 0 : b 0 = b 0/q, сбалансировав значения || b 0||^ и || a i||^, i = 1, 2, ...,n, где q > 0 — некоторое число. Тогда новое начальное значение переменной xn+1 будет равно q. Переменную xn+1 нельзя оставлять небазисной, так как она не равна своему граничному значению. Поэтому, прежде чем устранить недопустимость переменной xn+1 , введем ее в базис, заменив ею одну из базисных переменных. Для этого необходимо заменить вектор b0 на один из базисных столбцов, так чтобы не была нарушена невырожденность базисной матрицы и заменяемая базисная переменная xBi имела значение αBi или βBi .

Известно, что матрица B останется невырожденной при замене базисного столбца с номером i в базисе на столбец b0 если i-я компонента вектора B-1b0 не равна нулю. Рассмотрим вектор f = B- 1b0 = B- 1(Br/q) = r/q и определим множество J номеров базисных переменных, таких что для любого j Е J XBj = aBj или XBj = pBj. Множество J не пусто, так как в противном случае вектор b0 был бы равен нулю. Пусть I — множество ведущих элементов в столбцах множества J, i0 = arg max | fi | и j0 Е J — номер столбца с номером i∈I ведущего элемента i0 . Тогда столбец aj0 можно вывести из матрицы B и перевести в разряд небазисных, а столбец b0 ввести в базис с номером ведущего элемента i0 . Новая базисная матрица невырождена, так как |fi0| = max |xBi — XBi|/q.

i

Последний этап фазы I состоит в исключении из базиса искусственной переменной x n +1 при условии допустимости всех остальных базисных переменных. С этой целью используем алгоритм, предложенный в [1]. В данном алгоритме на каждой итерации величина сдвига вдоль выбранного направления вычисляется таким образом, чтобы суммарная величина отклонений базисных переменных от их отрезков допустимости была минимальной. На каждой итерации фазы I коэффициенты целевой функции, подлежащей минимизации, задаются в виде

{ — 1 , если x i < a i , + 1 , если x i > e i , 0 в остальных случаях.

Напомним, что дополнительная переменная x i имеет границы допустимости a i = 0 , e i = + то , а искусственная — a i = e i = 0. Коэффициенты c i используются для вычисления относительных оценок d j небазисных столбцов a j в модифицированном симплекс-методе [1]. На основе значений d j принимается решение о целесообразности ввода в базис столбца a j . Если на каком-либо шаге ни один небазисный столбец не может быть введен в базис (выполнен признак оптимальности), то полученное решение является оптимальным. Будем считать, что при X j = 0 j -я свободная переменная ( a j = —то , P j = + то ) может быть небазисной, а знак относительной оценки d j при выборе j -го столбца для ввода в базис несуществен. В оптимальном решении d j свободной небазисной переменной x j должно быть равно нулю.

Пусть на текущей итерации для ввода в базис выбран небазисный столбец aj . Тогда, как известно, вектор сдвига pB базисных переменных можно вычислить по формуле pB = -B-1 aj . Величину сдвига λ вдоль направления pB будем выбирать из условия минимума суммы отклонений J^ 5i (Ib — список базисных переменных) вектора Xв = xв + Apв от i∈IB параллелепипеда αB ≤ xB ≤ βB , где

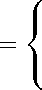
^α Bi

^X Bi

^{- x} Bi ^{, -} β Bi ^,

если x _Bi < α _Bi , если X Bi > в Bi , в остальных случаях.

Будем считать, что небазисная переменная x _Nj , которая вводится в базис, не нарушает границы допустимости, т. е. выполняется условие λ ≤ β _Nj - α _Nj .

Задача минимизации    δi сводится к задаче минимизации кусочно-линейной выпуклой i∈IB функции ф (x) одной переменной при условии x > 0. Функция ф является суммой кусочнолинейных функций ф,, определенных для базисных переменных xi (i Е Ib ):

• 1.    Если x _Bi < a _Bi и p _Bi <  0, то ф , ( x ) = 0.

• 2.    Если x _Bi < a _Bi и p _Bi >  0, то

  { Р в, ( Y i - x ) , Pb, ( x — n i ) , 0 ,

  
  

  если x < γ i , если x > η i , если γ i ≤ x ≤ η i ,

  
  

• 3.    Если x _Bi > e Bi и p _Bi >  0, то ф _i ( x ) = 0.

• 4.    Если x _Bi > e Bi и p _Bi <  0, то

  { — Р в, ( Y i — x ) ,

  — Р в, ( x — n i ) , 0 ,

  
  

  если x < γ i , если x > η i , если γ _i ≤ x ≤ η _i ,

  
  

• 5.    Если α Bi ≤ x Bi ≤ β Bi , то

• 6.    Если p _Bi = 0, то ф , ( x ) = 0.

где Y i = ( a Bi - x Bi ) /р в, ; n i = ( в Bi — x Bi ) /Р в, •

где Y i = — ( x i — e Bi ) /P Bi ; n i = — ( x Bi — a Bi ) /р в, .

ф, (x )={ lPBil( x- ni) , если x > ηi , если x ≤ ηi ,

где

= f (xBi - aBi)/PBi,  если рв, < 0, ni    ( (eBi — xb,)/рв,,  если PBi > 0.

Упорядочим величины Y i , n i ( i = 1 • 2 , • • • ,m ) по возрастанию их значений, запомним в соответствующем порядке номера переменных и обозначим через σ i элементы отсортированного массива. Тогда на каждом отрезке [ a i , a i ₊₁ ] функция ф линейна, а в точках ст, имеет изломы: ф (0) = ^ р в, — IL Pb, • Здесь 1 1 = { i : xb, < a b, } ; 1 2 = { i : xb, > в в, } . Нетрудно i ∈ I 2           i ∈ I 1

проверить, что ф (0) равна относительной оценке небазисного столбца, вводимого в базис: d j = C Nj — c B B — ¹ a j = c в P в = ф (0).

Целью минимизации функции ϕ является нахождение номера переменной, которая покидает список базисных столбцов, и величины сдвига вдоль pв. Для этого последовательно по i возрастанию индекса перебираются элементы а, и вычисляются величины т, = ф(0) — IL Рв,к, к =1

где i k — номер базисной переменной, стоящей на k -м месте после сортировки. Перебор осуществляется до тех пор, пока либо величина τ i перестанет быть положительной, либо величина а , станет больше e Nj — a Nj . В первом случае номер переменной i k , при котором т , _к <  0, выбирается в качестве номера столбца, выводимого из базисной матрицы, а в качестве искомой величины сдвига λ ^∗ вдоль вектора p B выбирается σ i _k . Если после перебора всех σ i величина τ i остается положительной, то в качестве λ ^∗ выбирается β Nj - α Nj и состав базиса не меняется, а небазисная переменная x Nj меняет свое граничное значение.

Фаза I считается законченной, если на некоторой итерации значения всех базисных переменных находятся в пределах своих границ допустимости, что означает принадлежность найденной точки множеству, определенному условиями (1) и (2), или если существуют недопустимые базисные переменные, при этом все относительные оценки небазисных переменных удовлетворяют условию оптимальности, что соответствует отсутствию допустимого решения в исходной задаче.

Вернемся к задаче построения начальной базисной матрицы B . Суть задачи состоит в следующем: из всего набора столбцов матрицы A следует выбрать m линейно независимых, так чтобы степень заполненности матрицы B ^{- 1} незначительно превышала степень заполненности матрицы B , а численная устойчивость разложения матрицы B ¹ = U - ¹ L - ¹ была достаточно высокой. Для решения данной задачи используем процедуру перепостроения обратных базисных матриц P ³ (preassigned pivot procedure) [2], модифицировав ее с целью увеличения численной устойчивости разложения B - ¹ = U - ¹ L - 1 . Процедура P ³ представляет собой эвристический алгоритм приведения с помощью перестановок строк и столбцов матрицы B к виду, по возможности близкому к нижней треугольной матрице. При этом предпринимается попытка минимизировать как число столбцов, имеющих ненулевые элементы над главной диагональю, так и количество ненулей в этих столбцах над главной диагональю. Столбцы, не имеющие ненулевых элементов над главной диагональю, называются нормальными, а имеющие — столбцами-выступами. Если матрица B состоит из нормальных столбцов и столбцов-выступов, причем последние расположены в порядке возрастания высоты столбцов, то новые ненулевые элементы в матрице B ^{- 1} могут возникнуть только в столбцах, которые соответствуют столбцам-выступам матрицы B , причем на месте нулевых элементов над главной диагональю. В данном случае к — высота столбца a j , если a kj = 0 и a ij = 0 при i < к .

После упорядочивания строк и столбцов ведущие элементы выбираются на главной диагонали сверху вниз и слева направо. Однако при таком правиле выбора ведущих элементов обеспечить численную устойчивость разложения матрицы B-1 = U-1L-1 достаточно трудно. Поэтому при получении очередного ведущего элемента нужно проконтролировать его величину и в случае нарушения допустимого уровня перевести столбец в резерв, чтобы иметь возможность использовать его в более подходящих условиях. Для проверки величины ведущего элемента можно использовать стандартный контроль ведущих элементов на устойчивость и отложить использование столбца, если ведущий элемент gi не удовлетворяет условию \gi\ > u max |gk|, где 0 < и < 1; K — список индексов столбцов, для которых k∈K еще не назначены ведущие элементы. В конце процесса разложения ведущие элементы в отложенных столбцах определяются путем частичного выбора в столбцах.

Описанная модификация процедуры P ³ использовалась в качестве процедуры перепо-строения обратной базисной матрицы в первых версиях пакетов программ для решения задач линейного и квадратичного программирования и их целочисленных вариантов [3, 4].

Применение модифицированной процедуры P ³ для формирования начальной матрицы B из столбцов матрицы A упрощается за счет того, что на каждом шаге список столбцов-кандидатов на ввод в базис шире текущего списка кандидатов при перепостроении обратной базисной матрицы. При этом в рассматриваемом случае существует больше возможностей при наборе столбцов в так называемый нижний треугольник. Кандидатом на включение в “нижний треугольник” в текущий момент является столбец, у которого для всех номеров ненулевых элементов (кроме одного) уже определены ведущие элементы.

Процессы формирования начальной базисной матрицы B и вычисления вектора b* можно модифицировать, выполняя их параллельно. На каждом шаге по правилам процедуры P 3 набираем множество J — список номеров небазисных столбцов-кандидатов на ввод в базис, прошедших стандартный контроль устойчивости. Затем для каждого j ∈ J вычисля- ем значение j-й переменной xj по текущим значениям остальных переменных. В качестве первоначального значения всем небазисным переменным xj присваиваем значения xj, опре деленные в (4). Для ввода в базис выбираем столбец с номером j о = arg min {dj || a j ||^}, где jeJ

5j — величина отклонения, определенная в (5); вектор b* пересчитывается с учетом 5j0, а в качестве нового значения xj0 выбирается величина xj0 =

^α j 0 ^, β j 0 , ^x j 0 ^,

если xj0 <αj0 , если xj0 >βj0 , если αj0 ≤ xj0 ≤ βj0 .

Данная процедура позволяет ожидать, что в конечном счете может быть получено наименьшее возможное значение || b * || ^ .

Последняя модификация процессов построения начальной базисной матрицы B и вычисления вектора b * , а также процедура устранения недопустимости, описанная выше, были использованы для одного из двух вариантов построения начального допустимого базиса во всех пакетах программ при решении задач оптимизации с линейными ограничениями [3–5]. Результаты расчетов показывают высокую численную устойчивость вычислительного процесса построения начального базиса.