Об одном способе регулирования остаточных напряжений в стеклующихся конструкциях

Для описания термомеханического поведения стеклующейся среды используется модель упругого приближения, учитывающая эффект «замораживания» деформаций при охлаждении материала и плавность релаксационного перехода, завершенность которого описывается сте- пенью стеклования N . Основные аспекты, связанные с построением и использованием данной модели в прикладных технологических задачах, изложены в работах [1–14]. Методика оптимизации остаточных напряжений в изделиях из стеклующихся полимерных материалов внешним силовым воздействием описана в [15]. Там же для иллюстрации возможностей предложенного алгоритма минимизации остаточных напряжений решена одномерная модельная задача поиска оптимального кинематического воздействия для неравномерно охлаждаемого пакета стеклующихся стержней с двумя видами управляющего воздействия в виде кусочно-линейных функций от времени. В работе [16] модель оптимизации применена для уменьшения остаточного прогиба неравномерно охлаждаемой в воде круглой пластинки. При этом регулирующее давление интерполируется полиномиальной функцией времени.

В данной работе рассматривается пример возможного использования предложенной методики оптимального управления остаточным НДС, в котором, в отличие от [15], [16], на вид функциональной зависимости от времени управляющей нагрузки не накладывается дополнительных ограничений.

Рассматривается процесс неравномерного осесимметричного охлаждения в воде круглой пластинки из эпоксидной смолы ЭД-20 с размерами R = 37,5 мм, H = 6,5 мм (рис. 1). В соответствии с программой эксперимента, описанного в [12], подготовленный образец нагревается до 150-170 ° C (температура, превышающая условную температуру начала стеклования T g 1 , при которой степень стеклования N(T > T g 1 ) = 0 [1]) и затем охлаждается путем погружения в воду нижней поверхности пластины. Результаты опыта [12] свидетельствуют, что как во время, так и по окончании охлаждения в конструкции возникают прогибы порядка 1 мм, обусловленные существенными градиентами температуры по толщине круглой пластинки

Поставим задачу оптимизации остаточного деформированного состояния в следующей формулировке: с помощью переменного во времени силового воздействия равномерно распределенной поверхностной нагрузкой p(t) требуется минимизировать отклонение от плоскостности верхней поверхности образца вида Uz (r) = uz (r, H) - uz (0, H) (см. рис. 1). При этом будем полагать, что взаимным влиянием дополнительного силового воздействия и температурного поля можно пре- небречь (возникающие в конструкции температурные деформации пластины не изменяют значение приложенной нагрузки, а тепловыделение, обусловленное диссипацией энергии дополнительного силового воздействия, пренебрежимо мало).

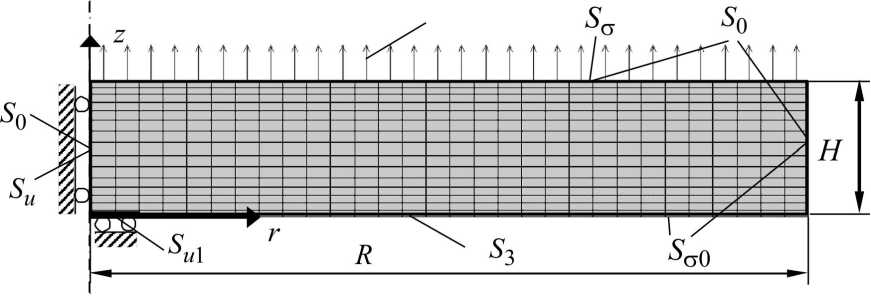
Рис. 1. Расчетная схема задачи

Для описания термомеханического поведения материала образца используем предложенную ранее модель упругого приближения вида [1]

_           N ( t )_

d( t ) = (⁴ C 1 + ⁴ C ₂ N ( t )) -8 ( t ) - ⁴ C ₂ •• J 8 ( т ) dN ( т ),            (1)

где ⁴ C ₂ = ⁴ C g - ⁴ 6 1 ; ⁴ C_g , ⁴ 6 1 - тензоры упругих констант материала в стеклообразном и высокоэластичном состояниях соответственно; 8 ( t ) = 8 -8 _T ; 8 , 8 T - тензоры полных и температурных деформаций со-

T ( t )

ответственно; еTij = j aj(т)dT(т); aj = аЪц; a - коэффициент темпе-T ратурного расширения; Ъц - символ Кронекера; с>(t) - тензор напря жений; T(t), To - текущая и начальная температуры соответственно; t - время. Связь между степенью стеклования N и температурой T можно описать, например, зависимостью [1]

N ( T , T ) = ^

1 - 0,5exp (^- T p),

^- ( ^{T -} Tg ( Т )) 0,5exp (— ^— ) ,

Tg,

g ’

где у - параметр, определяющий ширину интервала стеклования, Tg - температура стеклования.

Для определения остаточного напряженно-деформированного состояния конструкции с учетом сделанных допущений требуется последовательно решить две краевых задачи: нестационарной теплопроводности и на ее основе - расчет напряженно-деформированного состояния (НДС).

Нестационарное температурное поле T( x , t ) в области Q определяется из решения задачи теплопроводности:

T(x, t) = a2AT(x, t), xeQ, t e(0, t*],(3)

sup( T (x, t *)) < Tg 2,(4)

x eQ

T (x,0) = To; T (x, t) = Tfin, t > t *,(5)

Xn-grad(T) = h(T(x,t)-Ts(t)), xe S3,(6)

n-grad(T) = 0, xeSo,(7)

где T_{g 2} - условная температура конца стеклования ( N ( T > T_{g 2}) = 1 ).

В работе [15] показано, что для материалов, имеющих физические соотношения вида (1), в силу физической и геометрической линейности задачи расчета НДС можно применить принцип суперпозиции раздельных решений «температурной» и «силовой» задач. Разобьем интервал времени до момента окончательного охлаждения [0, t*] на Nt не обязательно равных подынтервалов. Под «силовой» понимается постановка задачи определения НДС вида div 5c(x,tk) = 0, xeQ,(8)

5s(x,tk) = ((V5u(x,tk))T + V5u(x,tk))/2 ,(9)

5u(x,tk)-n(x) = 0, xeSuUS^,(10)

5a(x,tk)-n(x) = 5p(tk)-n(x), xeSa ; 5

где 5p(tk) = p(tk) - p(tk-1) - приращение величины внешней распределенной нагрузки на k -м шаге по времени; n(x) - вектор внешней нормали. Главными отличительными признаками данной постановки яв- ляется включение внешнего силового воздействия при отсутствии температурных деформаций.

«Температурная» краевая задача также решается на каждом временном шаге и предполагает свободное (без регулирующей нагрузки p(t)) охлаждение конструкции:

div 86(x,tk) = 0, xeQ,	(13)
8e(x, tk) = ((V8u(x, tk)) T + V8u(x, tk ))/2,	(14)
8u(x, tk) -n(x) = 0, xeSuU Sul,	(15)
8<6(x, tk) -n(x) = 0, xeSaU Sao,	(16)
8<6 (tk ) = (4<?1 +4<C2 N (tk ))-86 (tk),	(17)

-                                T (tk)         а а где 8в = 8е-8eT; 8вT (tk) = J a(T)EdT; E - единичный тензор второ-

T (tk -1)

го ранга.

Остаточные напряжения и перемещения в момент полного остывания t* вычисляются в соответствии с [15] как суперпозиция «силового» и «температурного» решений:

u(x, t *)=u ^P (x, t *)+u ^T (x, t *), 6(x, t *) = 6 ^P (x, t *) + <6^T (x, t *).

При этом в силу линейности задачи каждое из слагаемых в (18) может быть определено как сумма приращений перемещений и напряжений на каждом шаге по времени от соответствующих приращений температуры и давления

Nt                                 Nt uP(х,t*)=^8uP(x,tk), 6P(x,t*)= ^86P(xtkh         (19)

k=1                                      k=1

Nt                             Nt uT (x, t*) = У 8uT (x, tk), 6T (x, t*) = ^86T (x, tk ),

(8)-(12);

k=1

k=1

где 8u^P (x, t_k), 86^P (x, t_k) - решение «силовой» задачи

8u^T (x, t_k), 8<6^T (x, t_k) - решение «температурной» задачи (13)-(17).

С учетом сказанного задача безусловной оптимизации остаточных перемещений модели (8)-(17) управляющим воздействием p(t) формулируется в виде

Ф(p(t)) = J [F(uT(x, t*) + u^P(x,t*))]²dS ^min ,          (21)

Sc где Sc - поверхность, на которой контролируется плоскостность образца; F(u) - некоторая скалярная функция вектора перемещений. В соответствии с условием задачи для контроля плоскостности образца после охлаждения выбрана осевая компонента вектора перемещений:

F (u)=Uz ( r, H).

Для конечно-элементной реализации поставленной краевой задачи используется программный комплекс ANSYS. В качестве базового выбран элемент PLANE42 с опцией осевой симметрии. Конечноэлементная сетка представлена на рис. 1. Термомеханические свойства материала взяты из [10]. Теплофизические свойства в соответствии с [17] имеют следующие значения: Х = 0,19 Вт/(м^К), c = 1000 Дж/(кгК), р = 1200 кг/м³.

Пространственная дискретизация при конечно-элементных расчетах сводит задачу (21) к решению системы линейных уравнений вида [C_p ]{P} = {Dp } относительно вектора управляющей нагрузки {р} размерностью, равной числу шагов по времени Nt. Матрица [Cp ], как показал анализ, является плохо обусловленной, что характерно для обратных задач, к которым относится рассматриваемая задача [18].

Учитывая (19), получим выражение для остаточных перемещений в результате решения «силовой» задачи

NtNt u P (x,1) = Z5u P (x tk ) = £ 5ПP (x tk ) APk,            (22)

к=1                    к=1

где 5й^р (x, tk) - решение «силовой» задачи (8)-(12) при единичном приращении внешней нагрузки Apk =1. Тогда задача оптимизации (21) преобразуется к следующей дискретной форме: