Об одном статистическом алгоритме анализа нестационарных процессов

Большое количество процессов, происходящих в окружающем мире, относятся к случайным нестационарным явлениям. Особым классом нестационарных процессов являются переходные процессы. Это различные ударные и взрывные явления, начало движения и остановка железнодорожных составов, разделение ракет-носителей, авиационное транспортирование различных грузов и т. д. Как правило, переходные процессы содержат и стационарную составляющую [1].

Алгоритмы обработки стационарных и нестационарных процессов имеют существенные различия, поэтому на первом этапе анализа любых временных зависимостей необходимо разделять стационарные и нестационарные составляющие исследуемых процессов. Известно, что статистическая достоверность результатов должна подтверждаться на достаточно большом числе реализаций. Например, число опытов (реализаций) h при доверительной вероятности Р должно быть не менее значений приведенных ниже [2]:

• -Р = 0,8, h= 20;

• - Р = 0,9, 0 =40;

Р 0,95, h 80;

Р 0,98, 0 200.

При этом характеристики внешних воздействующих факторов должны быть равномерно распределены во всем возможном диапазоне величин.

Однако на практике чаще приходится сталкиваться со сравнительно небольшим и даже малым числом опытов. В этом случае для определения характеристик случайных процессов по результатам небольшого числа опытов используются те же формулы, которые применяются и при большом числе опытов. В результате ставится дополнительная задача оценки точности получаемых из опыта характеристик [3].

Цалее рассмотрим алгоритм статистического анализа переходных процессов на примере исследования воздействий, возникающих при авиационном транспортировании специальных грузов самолетом Ил-76 в режиме взлета-посадки.

Суть алгоритма состоит в следующем. Имеется набор зависимостей ускорений от времени (набор временных рядов), например полученных на опорах груза в результате измерений при авиационном транспортировании для этапа взлета-посадки. Количество реализаций составляет выборку из 12 случаев транспортирования (рис. 1).

Цля каждой точки контроля по всем имеющимся случаям измерений формируется псевдоисходный процесс длительностью, равной их общей длительности, после чего из созданного псевдоисходного процесса с помощью датчика случайных чисел формируются множества фиктивных выборок. По фиктивным выборкам проводится оценка изменчивости параметра генеральной совокупности по изменчивости его оценок, полученных в фиктивных выборках, и делается заключение о стационарности полученного процесса. Цлительность фиктивных выборок по времени составляет 2.. .4 с.

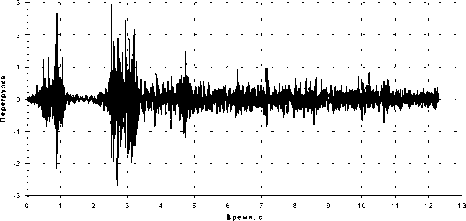
Рис. 1. Типовой график зависимости ускорения от времени на задней опоре груза при посадке самолета Ил-76

Оценка стационарности проводится по стандартным методикам: вычисление среднего, дисперсии и т. д. В большинстве случаев для практики достаточно получить оценку стационарности по среднему и дисперсии.

При выводе о нестационарности процесса из созданного псевдоисходного процесса исключаются составляющие с уровнями выше некоторой заданной величины. Затем повторяется процедура исследования стационарности рассматриваемого процесса, и при необходимости продолжается исключение максимальных составляющих до получения стационарного псевдоисходного процесса. Цостаточным шагом по амплитуде ускорения можно принять его значение в 0,1 g . Количество фиктивных выборок должно увеличиваться до тех пор, пока погрешность не стабилизируется. Исследование результатов измерений взлета-посадки самолета Ил-76 показало, что выделение участков с уровнями виброускорений, превышающими ±1 g , позволяет далее оценивать этот процесс как стационарный (рис. 2).

Таким образом, имеются два процесса: начальный псевдоисходный процесс и полученный из него стационарный псевдоисходный процесс. Цалее проводится Фурье-преобразование начального и полученного псевдо-исходных процессов, и из коэффициентов Фурье-преоб- разования начального псевдоисходного процесса вычитаются коэффициенты Фурье-преобразования стационарной части псевдоисходного процесса. В результате такой операции в исходном процессе остаются только нестационарные составляющие. Выполнение обратного преобразования Фурье позволяет получить нестационарную составляющую часть псевдоисходного процесса в виде временной зависимости.

строились отдельно для стационарной и нестационарной составляющих рассматриваемого процесса и для полного псевдоисходного процесса. Как и при проверке стационарности, с помощью датчика случайных чисел формируются множества фиктивных выборок, причем количество фиктивных выборок должно увеличиваться до тех пор, пока погрешность не стабилизируется.

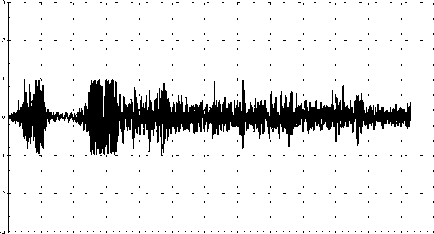
О           1           2           3           4           5           6           7           8           9           10          11           12          13

Время, с

Рис. 2. Типовой вибрографик ускорений с исключенными значениями выше ±1 g

О 10   20   30   40   30   60   70   60   90  100 110 120 130 140 130 160 170 160 190 200 210 220 230 240 230 260 270 260 290 300 310

Частота. Гц

Рис. 4. Огибающий ударный спектр ускорений по направлению движения самолета

В результате из одного псевдоисходного процесса получаются два процесса: стационарный и нестационарный, дальнейшая обработка которых проводится по алгоритмам, предназначенным для обработки соответствующих процессов.

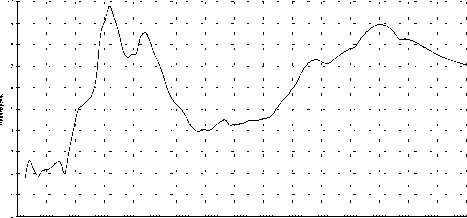
Для стационарного процесса это, в первую очередь, получение спектральной плотности мощности виброускорений (рис. 3), а также среднеквадратических значений в полосах частот и гистограмм распределения экстремумов ускорений. Дополнительно проводится построение автокорреляционных функций и взаимных корреляционных функций между значениями вибрационных нагрузок на передней и задней опорах для рассматриваемых временных участков по различным направлениям.

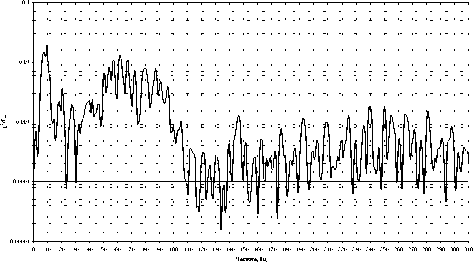
Рис. 3. Огибающая значений спектральной плотности (типовая спектральная плотность) мощности виброускорения для стационарной составляющей по направлению движения самолета

Для нестационарного процесса выполняется построение ударного спектра ускорений, огибающих максимальных и минимальных значений ударных спектров ускорений для различных временных участков и направлений воздействия (рис. 4), а также построение гистограмм распределения текущих значений ускорений (рис. 5). Следует отметить, что гистограммы экстремумов ускорений

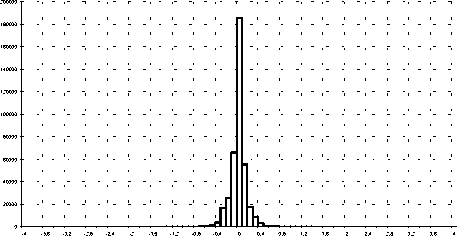
Рис. 5. Гистограмма амплитуд виброускорений по направлению движения самолета для начального псевдоисходного процесса (12 случаев транспортирования)

Для анализа как стационарных, так нестационарных процессов применялся вейвлет-анализ, что позволило связать максимумы ускорений по времени и частоте [4].

Рассмотренный алгоритм дополняет хорошо известный подход к анализу нестационарных процессов, предложенный В. В. Болотиным для исследования сейсмических нагрузок, когда исследуемый процесс представляется в виде произведения функций, описывающих стационарные случайные процессы с заданными спектральными плотностями, и детерминистических функций времени [5]. Одним из наиболее простых таких представлений является формула a (t) А е -“р( t)ц( t), гдеЛ 0, с - некоторые положительные постоянные; ф(t) -стационарная случайная функция времени; ^(t) - функция Хевисайда.

Этап взлета и посадки имеет четко выраженный нестационарный характер, что обусловливается как ударными воздействиями на самолет в момент касания взлетно-посадочной полосы, так и достаточно резким торможением. Причины возникновения вибрационного нагружения транспортируемого груза имеют различную природу и их несколько. Поэтому представить описание такого процесса одной функцией невозможно. Был проведен дополнительный анализ стационарной составляющей псевдоисходного процесса в частотной области. По результатам предварительной обработки виброграмм воздействие на груз при взлете и посадке может быть представлено в следующем виде:

F ( t , w )= А ( t , w )+ В ( t , w )+ С ( t , w )+ 5 ( t , w ), где В ( t , w ) - широкополосная случайная составляющая, изменяющаяся в диапазоне 100.. .310 Гц по амплитуде ±1 g , в диапазоне 3.100 Гц ±0,5 g ; 5 ( t , w ) - нормальный белый шум с дисперсией 2,5 % от дисперсии суммарного про-цесса; А ( t , w ) - узкополосная случайная составляющая, изменяющаяся в диапазоне 50.80 Гц для продольных колебаний и 80.160 Гц для поперечных колебаний, амплитуда изменяется в диапазоне ± 2,5 g; С ( t , w ) - низкочастотная узкополосная случайная составляющая, изменяющаяся в диапазонах 5.7 Гц и 15.20 Гц, амплитуда суммарного сигнала изменяется в пределах ±0,4 g.

Выражение для F(t, w) может быть представлено в виде F (t, w) ^А • exp [-а (t -11)]sin (wt + a) + В sin (ut + b) + + С sin (vt + c) + 5(t), гдеА, В, С-константы, соответствующие максимальным значениям ускорений; a,b, c - случайные переменные.

Для анализа рассматриваемых процессов использовался хорошо известный пакет MATLAB. Необходимые для проведения расчетов макросы были написаны на языке Simulink.

Проведенная по представленному алгоритму обработка показала, что анализ псевдоисходных процессов, состоящих из данных по 4.5 и 12 случаям транспортирования, дает результаты, которые практически не отличаются друг от друга. Следует отметить, что полученные уровни воздействий на транспортируемый груз примерно в 3.4 раза (в зависимости от частотного диапазона) ниже представленных в нормах на груз. При этом задание режима испытаний груза при его отработке на транспортирование проводят по точкам контроля, которые использовались для формирования псевдоисходного процесса.

Таким образом, предложенный алгоритм позволяет проводить более точную обработку временных рядов, полученных при регистрации переходных процессов. Для реализации такого алгоритма требуется разработка автоматизированной системы обработки данных, для чего необходимо создать базу данных (БД), которая включала бы всю исходную информацию в структурированном виде, которая содержит данные об исследуемых процессах, все промежуточные данные и окончательные результаты обработки. Для удобства хранения и доступа создаваемая база данных должна быть объектно-ориентированной и состоять из головного файла, файлов таблиц и файлов индексов таблиц.

Целью разработки любой базы данных является хранение и использование информации о какой-либо предметной области. Целью разрабатываемой БД в нашем случае является хранение и использование различных данных об исходных временных рядах, результаты промежуточной и окончательной обработки различных параметров, а также интеграция работы прикладных программ (подсистем), которые производят оценочные расчеты этих параметров.

Работа с базой данных организуется по принципу клиент-сервер; в качестве клиента выступает подпрограмма оценки одного из параметров. Подсистемы обращаются к БД, считывают данные, обрабатывают, а затем записывают информацию в БД или файлы результатов. Очевидно, что такая база данных должна иметь достаточно сложную структуру, так как с ней работает несколько подсистем, которые рассчитывают различные параметры. При проектировании БД анализируемый процесс раскладывается на отдельные типы объектов, соответствующим типам обработки. То, какие свойства объекта необходимо хранить в таблицах, определяется типом объектов и тем, какие подсистемы будут работать с таблицами, а также с информационными потоками между подсистемами. При стратегическом планировании БД должны учитываться требования на данные всех подсистем, которые будут работать с БД. Такой подход избавляет от необходимости переписывать уже имеющиеся приложения (подсистемы) при добавлении в интегрированную многоуровневую систему новой подсистемы [6; 7].