Об одном уравнении состояния и внутреннем давлении в металлах

При решении практических задач, связанных с использованием металлов как конструкционных материалов, возникает потребность расчета термодинамических свойств при заданных температурных и механических нагрузках. Для этих целей используются различные полуэмпиричес-кие модели уравнения состояния, отражающие функциональную связь между температурой Т , давлением Р , объемом V и плотностью р в состоянии термодинамического равновесия.

Уравнение состояния допускает возможность рассчитать такие величины, как объемный коэффициент термического расширения в , модуль всестороннего сжатия К , представляющего собой силовую характеристику межатомного взаимодействия и установить связь между коэффициентами в и К • По определению объемный коэффициент теплового расширения:

R 1 Р V )

в = 3а = —-I — I m V (д T ) P ’ (1)

где а - линейный коэффициент теплового расширения. Объемная упругость или сжимаемость:

1     1 Гd V )

--- —--•  ---- .

К V (д P ) _T

Из (1) и (2) следует, что между величинами в и К существует связь вида:

5Р в-К = — . д Т

Модуль всестороннего сжатия и объемный коэффициент теплового расширения являются

важными термодинамическими характеристиками вещества. В этой связи возникает естественная желание увязать упругость системы и ее тепловое расширение с особыми свойствами потенциальной энергии, а именно, с ее чувствительностью к закону расположения частиц в пространстве. Принято считать, что статистическая механика способна описать термодинамические свойства любой системы частиц, если известны силы, действующие между атомами. Трудности на этом пути связаны с учетом всех взаимодействий в реальных кристаллах. Решение задачи в основном сводится к заданию более или менее правдоподобного потенциала межатомного взаимодействия с последующим сравнением результатов расчета с экспериментальными данными. Потенциал должен удовлетворять двум основным условиям: иметь минимум при некотором значении r₀ , чтобы обеспечить устойчивость кристаллической решетки по отношению к малым деформациям и обладать асимметрией, чтобы обеспечить ангармонизм в колебаниях атомов. В строго гармоническом кристалле частоты нормальных мод не зависят от объема, что приводит к отсутствию эффекта теплового расширения. Для металлов в ангармонических кристаллах уравнение (1) приближенно можно представить в виде [1]:

1 < ■ 2

ion эл в = К (ГС" + 3 Си ) , (4) где Г - коэффициент Грюнайзена, C™ и C3” - решеточная и электронная удельные теплоемкости.

В классической теории упругости пренебрегают микроскопической атомной структурой твердого тела, рассматривая его как непрерывную среду. Для изотропного твердого тела модуль

К =

Е

3(1 - 2 а )

рассматривается как коэффициент пропорциональности между деформацией и внешним давлением. Здесь Е – модуль Юнга, у – коэффициент Пуассона.

Таким образом, отсутствие возможности адекватного описания кристаллических систем в рамках решеточной модели служат достаточным стимулом для дальнейших теоретических исследований.

2. ОДНОУРОВНЕВАЯ МОДЕЛЬ КРИСТАЛЛИЧЕСКОЙ СИСТЕМЫ

F F f =- = E-

_N T _N

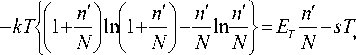
(8) где s – энтропия на атом в объёме системы.

Будем полагать, что растворение n' дырок равносильно изменению объёма на атом на величину д х . Если принять объём, занимаемый атомом при Т=0 , равным х₀ , то ОДСО можно выразить соотношением вида

n' _ Ди _ 3 A d ~ Д V

N "  и о = d 0 ~ V 0 .       ⁽⁹⁾

Будем полагать, что атомы кристаллической решетки находятся на одном энергетическом уровне, которому соответствует одинаковая плотность частиц с объемом

и

— n r

V

N ^,

где V – объем кристалла, N – число частиц, r – радиус сферы, содержащей одну частицу.

Но объём V является достаточно неопределённой величиной. Поэтому для характеристики физического состояния кристаллической системы удобнее пользоваться понятием плотности или понятием относительной доли свободного объёма Z (ОДСО).

Для получения уравнения состояния атомов в кристаллической системе будем опираться на некоторые положения дырочно-активационной теории Я.И. Френкеля [2, 3], согласно которой изменение объёма системы при нагревании связывается с “разрыхлением” структуры благодаря образованию и растворению “дырочного” микрообъёма. Изменение состояния даже одного электрона в системе будет сопровождаться возникновением вакантного места – “дырки”, как меры (или порции) дополнительного микрообъёма. Поэтому если в кристаллической системе содержится N атомов и n' “дырок”, то число способов растворения “дырочного” объёма в такой системе равно (N+n')! / N!n'! . Тогда свободную энергию системы можно представить в виде:

Здесь d0 и V0 – постоянная решётки и объём системы при Т=0. Уравнение (9) вытекает из выражения (6). С учётом (9) выражение (8) примет вид f _ P-и-5-kT{(1 + 5)ln(1 + 5)-5ln5} .(10)

Экстремум в (10) достигается при условии, если

f P ^u А¹

⁵ = 1 exp И ~‘J

Из (11) следует, что

P u _ kT ln

(

1+7

к ⁵ J

т.е внутреннее давление в системе пропорционально Т. При Z = 0,582 (58%) уравнение (12) переходит в уравнение состояния для идеального газа.

Допущение о растворимости “дырок” в объёме системы позволяет рассматривать термическое расширение как процесс растворения “дырочного” микрообъёма. Это позволяет уйти от рассмотрения ангармонизма в колебаниях атомов.

Рассмотрим малое изменение относительной доли свободного объема dт , представив это изменение в виде:

d 5 ^^^ dP +^ d u + ⁵ T _-B' dP + p dT ,(13) d P     du    ST                ^v '

(N + n ')!

- = n E_T - kT ln------—

^T               N ! - n '! ’

где    B ' = — ( 5 + 5 ² ) u + Р ^^

T ’   5 P

где k – постоянная Больцмана, а энергия E_T=Pх . Физический смысл этой формулы можно пояснить следующим образом. Растворение “дырочного” объёма в кристалле сопровождается увеличением объёма в котором локализовано движение атома. Равновесие в системе наступает при внутреннем давлении Р . Из (7) следует, что свободную энергию f на атом можно представить выражением вида:

- обобщенная сжимаемость,

3 ^{a _ e _ (}5 + 5 ^{2 )ln 1 + 7        (15)}

T           к    ⁵ J

– объемный коэффициент термического расширения.

При изотермическом сжатии из выражения (13) следует

- d5 _ B'dP .             (16)

Полагая d 5 = г и dP=P? , получим:

- 6 = 717 (5 + 5 ')

u + P — P' d P

.

Здесь 6 — деформация, Р? - внешнее давление. Слагаемое Р ( ди / д P ) P ' квадратично по давлению.

Опыт показывает, что для твердых тел существует область деформаций, в пределах которой выполняется закон Гука. Для металлов она составляет около 2-5% от объема образца. Полагая в этой области u = const , получим выражение

- 6 = ВР*,(18)

известное как закон Гука.

Здесь B = К - kT (5 + 52)

- сжимаемость в линейной области деформаций.

Так как, согласно (12), u = ( kT / P ) ln(1 + 1/ 5 ) , выражение (19) примет вид:

B = -1 (5 + 52 )lnf1 +11.(20)

P V 5 7

Выражения (15) и (20) симметричны. Разделив (15) на (20), получим зависимость (3) в виде:

Р

Р К = T .               (21)

Уравнение (21) позволяет непосредственно рассчитать величину внутреннего давления в кристаллической системе.

Таким образом, уравнения (1, 2, 3) можно представить в явном виде соотношениями (15, 19-21).

предположить, что при всестороннем сжатии такой системы основной вклад в сопротивление сжатию должна вносить кристаллическая фаза. В связи с этим объём х , содержащийся в (19), должен соответствовать объёму занимаемому атомом в кристаллической решётке в соответствии с её симметрией. Совместное решение уравнений (15) и (19) даёт возможность проверить это предположение.

Представим объем х в виде:

и = Ad ³ , (22) где А – параметр, величину которого требуется определить, d – постоянная кристаллической решетки. Из кристаллографии известно, что для ОЦК решеток А = 0,5, для ГЦК – А = 0,25.

Задача состоит в том, чтобы рассчитать величину параметра А и сопоставить его значение с кристаллографическими данными. По степени согласия величины А с кристаллографическими данными можно судить о достоверности предложенной модели.

Расчеты проводились для металлов с ОЦК, ГЦК и ГПУ решетками при температуре 300 К. В табл. 1 размещены данные о величине постоянной решетки d и модуле К для металлов с ОЦК и ГЦК решетками, взятые из справочников [4, 5]. В металлах с плотной упаковкой атомов (ГПУ решетка) симметрия кристалла характеризуется двумя значениями постоянной решетки – d и с . В табл. 2 представлены данные о величинах d , с и модуле К в металлах с ГПУ решеткой и алмаза.

Согласно (19) К~ ^—

»

1 d ³

, что физически оп-

3. ПРИМЕНЕНИЕ МОДЕЛИ К РАСЧЕТУ ОБЪЕМА Х

Кристаллическая система не является идеальной. Например, в поликристаллических материалах, кроме кристаллической фазы, имеются межзёренные границы, роль и значение которых предстоит ещё определить. Однако, разумно равдано. По данным табл. 1,2, такая зависимость наблюдается у группы щелочных металлов. Аналогичную тенденцию можно отметить у Zn, Mg, Bi и Co. У Ni, Pd и Pt – напротив, более высокому значению d соответствует более высокое значение К. У Au и Ag значения d почти совпадают. Однако, модуль К у Au в 1,6 раза выше, чем у Ag.

Для расчета ОДСО в металлах использовалось уравнение (15). Значение линейного коэф-

Таблица 1. Данные о постоянной решетки d и модуле К в металлах с ОЦК и ГЦК решетками

Элемент ОЦК	d •1010 м	K •10-9 Па	Элемент ГЦК	d •1010 м	К •10-9 Па
Li	3,51	11,80	Аl	4,05	73,40
Na	4,23	6,20	Аg	4,09	100,30
K	5,33	3,40	Au	4,08	164,20
α-Fe	2,87	171,11	Cu	3,61	137,00
Rb	5,59	2,66	Ni	3,52	180,26
Cs	6,05	1,62	Pd	3,89	181,00
Mo	3,15	253,10	Pt	3,92	263,00
W	3,16	300,10	Pb	4,95	42,353

Таблица 2. Данные о постоянных решетки d,c и модуле К в металлахс ГПУ решеткой и алмаза

Элемент ГПУ	Zn	Mg	Sn	Bi	Co	C
d •1010 м	2,66	3,21	5,82	4,75	2,51	3,57
с •1010 м	4,937	5,213	3,178		4,071	5,894
К •10-9 Па	61,46	35,06	55,7	33,3	167,1	560

Таблица 3. Значения α и теоретические значения ОДСО ζ для ОЦК и ГЦК металлов

Элемент ОЦК	α •106 K-1	ς •102	Элемент ГЦК	α •106 K-1	ς •102
Li	56	1,110	Al	22,7	0,354
Na	71	1,493	Ag	19	0,284
K	79,6	1,728	Au	14	0,197
α-Fe	12	0,169	Cu	16,5	0,242
Rb	90	2,030	Ni	13,5	0,195
Cs	97	2,170	Pd	11,6	0,163
Mo	6,2	0,077	Pt	9	0,120
W	4,6	0,055	Pb	28,5	0,478

Таблица 4. Значения α и теоретические значения ОДСО для металлов с ГПУ решеткой и алмаза

Элемент	Zn	Mg	Sn	Bi	Co	C
α •106 K-1	30,4	25,5	22,04	14,3	14,5	0,8
ς •102	0,519	0,42	0,349	0,212	0,212	0,0076

Таблица 5. Рассчитанные значения d³, объема х и параметра А в металлах с ОЦК и ГЦК решетками

Элемент ОЦК d3•1029 м3 υ•1029 м3 Аd Элемент ГЦК d3•1029 м3 υ•1029 м3 Аd Li 4,325 3,128 0,72 Al 6,643 1,593 0,24 Na 7,570 4,409 0,58 Ag 6,843 1,450 0,21 K 15,142 6,930 0,46 Au 6,793 1,280 0,19 α-Fe 2,364 1,180 0,50 Cu 4,700 1,250 0,26 Rb 17,770 8,155 0,47 Ni 4,474 1,176 0,26 Cs 22,140 11,780 0,53 Pd 5,886 1,400 0,24 Mo 3,126 2,076 0,66 Pt 6,023 1,310 0,22 W 3,155 2,500 0,79 Pb 12,130 1,900 0,17 фициента термического расширения α , также брались из справочников [4, 5]. Данные расчета ОДСО представлены в табл. 3, 4.

Сравнительный анализ данных табл. 1, 2 и табл. 3, 4 свидетельствует о явной зависимости модуля К от величины ОДСО. Например, самый высокий модуль К у алмаза и самый низкий у цезия. Отношение модулей К _C/ К _Cs = 272 и отношение ОДСО ζ _Cs / ζ _C = 285,5 почти совпадают. У Fe и Zn постоянные решеток близки друг к другу. Но модуль К _Fe в 2,9 раз выше, чем у К _Zn. При этом ОДСО у цинка в 3 раза

выше, чем у железа. Постоянные решеток у Li и Ni почти одинаковые, но модуль К _Ni в 14 раз превосходит модуль К _Li. Однако, величина ζ _Li всего в 6,15 раза превосходит значение ζ _Ni. Почти двукратное расхождение можно объяснить, если учесть, что параметр А в ОЦК решетке в два раза выше, чем в ГЦК решетке. Таким образом, чем выше значение ОДСО в металле, тем ниже модуль упругости К . Данные табл. 1, 2, 3, 4 позволяют рассчитать величину d³ , объем х и параметр А из выражений (19, 22). Результаты расчета представлены в табл. 5, 6.

Таблица 6. Рассчитанные значения d³ , объема х и параметра А для металлов с ГПУ решеткой и алмаза

Элемент	Zn	Mg	Sn	Bi	Co	C
d 3•1029 м3	1,882	3,310	19,710	10,720	1,581	4,550
c 3 •10 29 м 3	12,003	14,166	3,21	-	6,747	20,475
υ •1029 м3	1,292	2,806	2,123	5,870	1,167	9,732
A d	0,69	0,85	0,11	0,55	0,74	2,14
A с	0,11	0,2	0,66	-	0,17	0,47

4. РАСЧЁТ ВНУТРЕННЕГО ДАВЛЕНИЯ

Расчеты показывают, что совокупность значений параметра А в ОЦК металлах лежат в интервале значений от 0,46 до 0,79 и в среднем составляет около 0,59, что с хорошей степенью точности соответствует ожидаемому кристаллографическому значению, равному 0,5. Аналогично, для ГЦК металлов совокупность значений параметра А лежит в интервале от 0,17 до 0,26 и в среднем составляет значение, равное 0,22, что также

При расчёте давления используются общие принципы термодинамики, согласно которым, давление P = – (дF/дV)_T , где F=U-TS – свободная энергия. Так как энтропия S и внутренняя энергия U связаны соотношением

T (— J Id T J

(a и J V "Id T ^J V

хорошо соответствует ожидаемому значению, равному 0,25.

Несколько завышенные значения А получаются у вольфрама и молибдена, что возможно связано с неточностью в экспериментальной оценке значений модуля К и коэффициента линейного расширения а .

Несколько заниженные значения А получены для Аu и Pb. Для остальных элементов отклонения А от кристаллографического значения в среднем составляет около 4%.

В отношении металлов с ГПУ решеткой результаты расчета (табл. 6) менее очевидны. По данным табл. 6 эти металлы можно отнести и к

то давление можно выразить через внутреннюю энергию кристалла:

P =

-

T

A u - t d V         ^J_n

dT' d T' d T ‘

U ( TV )

металлам с ОЦК решеткой и к металлам с ГЦК решеткой.

Несколько неожиданный результат получен для углерода со структурой алмаза. Данные расчета дают параметр A_d = 2,14, что физически кажется абсурдным.

Если пр и нять объем на атом в решетке алмаза равным "d¹ d , то объем х должен содержать в себе четыр 6 е атома углерода. Поэтому жесткость

кристалла скорее всего следует увязывать с постоянной решетки c .

Таким образом, расчеты свидетельствуют о явной зависимости энергии Е_T от характера упаковки атомов в кристаллических системах.

Необходимо отметить сильную зависимость модуля К от величины ОДСО.

Как правило решение задачи сводится к заданию вида внутренней энергии, учитывающей вклад потенциальной энергии, тепловой и электронной. Такие модели содержат эмпирические параметры, которые лишают нас возможности судить о степени реалистичности таких моделей. В нашем случае внутреннее давление можно рассматривать как фактор, играющий определяющую роль в характере расположения частиц в пространстве. Это заключение непосредственно вытекает из того обстоятельства, что данные теоретического расчёта объёма х (табл. 5, 6) хорошо согласуются с кристаллографическими. Поэтому есть основания полагать, что рассчитанные ниже величины внутреннего давления в металлах соответствуют реальным значениям.

Для расчёта внутреннего давления в металлах достаточно воспользоваться уравнением (21). Результаты расчёта представлены в табл. 7.

Результаты расчёта свидетельствуют о высоком уровне внутреннего давления в металлах. Самое низкое давление у Cs и самое высокое у Ni. Отметим, что для группы щелочных металлов давление снижается с ростом массы атома. Обратная тенденция наблюдается для Al, Cu, Ag и Au.

Таблица 7. Рассчитанные значения давления Р в металлах с ОЦК, ГЦК и ГПУ решётками

Элемент ОЦК	Р , 103, кГ/см2	Элемент ГЦК	Р , 103, кГ/см2	Элемент ГПУ	Р , 103, кГ/см2
Li	5,87	Al	14,80	Zn	16,59
Na	3,91	Ag	16,92	Mg	7,94
K	2,40	Au	20,43	Sn	10,91
Rb	1,96	Cu	15,20	Bi	4,24
Cs	1,39	Ni	21,71	Co	21,52
α-Fe	18,24	Pd	18,64	C	3,98
Mo	13,92	Pt	21,02
W	12,26	Pb	10,72

ABOUT CONSTITUTIVE EQUATION AND INTRINSIC PRESSURE IN METALS

Boris Bertyaev, Candidate of Physics and Mathematics, Assistant Professor.

Igor Reut, Post-Graduate Student

5.    ЗАКЛЮЧЕНИЕ

Итак, термодинамический анализ металлов, выполненный в рамках одноуровневой модели кристаллической системы, позволил выявить связь симметрии кристаллической решётки с её тепловыми и механическими свойствами. Кристалл оказывается “растянутым” внутренним давлением при любой температуре. Причём уровень давления оказывается значительным и колеблется от 103 кГ/см2 до 104 кГ/см2. В этой связи встаёт вопрос о причинах механической устойчивости кристаллической системы. Ведь чтобы “удержать” деформированный кристалл к нему необходимо приложить отрицательное Ван-дер-Ваальсовое давление. Эту роль может выполнять

граница или поверхность кристалла. С формальной точки зрения, это означает введение в модель второго уровня. Но решение этой задачи выходит за рамки данной работы.