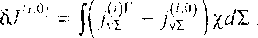Об определении линейных и нелинейных свойств неоднородных материалов

The following identification problems arc considered: electrical conductivity identification, linear and non-linear elasticity parameters, viscosity, thermal parameters. I'he approximate solution methods are developed, based on the Newton method and variational approach.

Проблема нахождения параметров или функций, характеризующих поведение однородных материалов, в настоящее время решена для широких классов определяющих уравнений, в том числе для материалов, обладающих геометрической и физической нелинейностью [1]. Однако для неоднородных материалов, физикомеханические свойства которых зависят от пространственных координат и. возможно, от времени, положение иное. В го же время знание указанных пространственных распределений необходимо как для формулировок точных постановок краевых и начально-краевых задач, так и для конструирования приближенных методов решения.

Источником неоднородности конструкционных материалов являются, прежде всего, технологические процессы их получения и обработки [2]. Кроме того, неоднородность, которую необходимо учитывать при построении более точных теорий поведения классических конструкционных материалов типа сталей, обусловлена их кристаллическим (поликристаллическим) строением. В современных композиционных материалах неоднородность определяется изначально их гетерогенностью. Особхю роль неоднородность структуры играет при построении теорий поведения биологических тканей, поскольку те или иные отклонения от «стандаргной» неоднородности являются основой для построения различных методов диагностики. Знание параметров неоднородности должно быть заложено как исходная информация в мезомеханику [3].

Точные методы решения данной проблемы стали развиваться относительно недавно, и основано это развитие на методах томографии [4-6]. В настоящей статье речь пойдет как раз о томографических методах решения проблемы неоднородности, представляющих собой важное и актуальное направление для ряда технических задач, задач биомедицинский диагностики и для многих задач об анализе природных процессов и техногенных катастроф.

Модельная задача

Рассмотрим в качестве модельной краевую задачу для обобщенного уравнения Лапласа

V(a(x)V

(1)

которое описывает распределение электрического потенциала ср = (р(.г) в области Q. материал в которой имеет электрическую проводимость ст. С помощью уравнения (1) можно построить математическую модель одного из современных методов диагностики - метода импедансной или потенциальной томографии [4]. Электрические схемы измерений в данном методе описаны в [4, 7].

Схема этих измерений такова. К поверхности диагностируемого тела (технической конструкции или биологического объекта) прикладывается некоторое распределение электрического потенциала, и измеряется соответствующее распределение электрического тока через поверхность. Естественно, что при технической реализации может быть использовано только конечное количество электродов, а при построении математической модели необходимо рассматривать сложную физическую задачу о контактном взаимодействии двух электропроводных тел. Для упрощения построения теории предполагают, что известно распределение электрического потенциала на всей поверхности X = Э£2 диагностируемого объекта:

ф(-^к=Фх>                            <2)

а также известно соответствующее распределение электрического тока у'у£на той же поверхности:

ф(х)-> ;vE(x), хе Z .                             (3)

Соответствие между' граничными токами и потенциалами устанавливается посредством либо решения задачи Дирихле (1)-(2), либо решения задачи Неймана для уравнения (I) с граничным условием

(4) dV где v - вектор единичной внешней нормали к поверхности X (точка означает скалярное произведение векторов), V - оператор Гамильтона.,

Поскольку основной задачей импедансной томографии является нахождение пространственного распределения проводимости а(х), а известной из эксперимента информацией являются граничные значения тока и потенциала, то математическая модель данного вида диагностики должна включать уравнение (1) и граничные условия (2) и (4), в которых неизвестными будут две функции а(х), ф(х). Следовательно, задача является нелинейной. Более того, единственного измерения оказывается недостаточным для однозначного ее решения. Данное утверждение сначала было установлено для конечномерного аналога поставленной задачи на основании известной из теоретической электротехники теоремы Телегена (по этому поводу см. работу Г8]). Применительно к рассматриваемой здесь континуальной постановке задачи высказанное утверждение означает, чго необходимо (теоретически) иметь бесконечное число граничных пар <ру, jvT для того, чтобы задача могла быть решена единственным образом. К счастью (и это впервые отмечено в работе [6]), пространство граничных потенциалов имеет счетный базис, что позволяет поставить задачу о доказательстве соответствующих аппроксимационных теорем, начиная с доказательства существования для случая конечного базиса.

Приведем три метода решения поставленной задачи.

• 1.    Лагранжев метод последовательных приближений

Пусть имеется набор соответствующих друг другу граничных пар )ф( -Pvt где число пар N может быть бесконечным; для конечного значения возникает, как уже отмечалось, проблема аппроксимации, которая, насколько нам известно, не решена.

Пометим верхним индексом "Р истинное распределение проводимости и соответствующие ему распределения потенциала внутри и на границе и распределение граничных токов:

G = o\

Приведем описание основных шагов итерационного процесса в варианте метода Бубнова - Галеркина. Процесс начинается с задания некоторого нулевого приближения проводимости:

о = о^°- (х), лей.

Кроме того, предполагается, что для всех функций базиса Qy' из эксперимента найдены соответствующие граничные токи f^¹ :

• а)    для каждой базисной функции фу' решаем задачу Дирихле с граничным условием:

ф1'"0'1 |£ = ^ (х), х s I.                                    (Д

По решению данной задачи вычисляем нулевые приближения граничных токов .

• б)    выбираем произвольную функцию %е №(£2) и вычисляем взвешенную с функцией х разность истинного распределения и нулевого приближения граничных токов (невязку):

  

Е

Формула Гаусса - Остроградского позволяет найти следующие выражения для ш-зязкш

Введем разности:

ост~<7^к -о'⁰¹, 5ф⁽" -рГ¹'' - ф¹’’⁰'                        (10)

и линеаризуем правые части в выражениях (9) по разностям (10):

г сИ^и:                              в t,?,Vq>^<-' ] • Vydil (ID

Заменяя знак приближенного равенства в (И') точным, получим два вариационных уравнения, второе из которых связывает две ней звестные функции (10) в облас ш £2:

• в)    считая формально функцию Оу известной, выразим все функции Зо^{1 1} через 8у. Из второго из уравнений (11) видно, что эта операция эквивалентна решению задач Дирихле для уравнения

V • [а(0) V(3

с нулевым граничным условием для 8(р(,). Записывая решения этих задач в виде 8ф<у’ = L(,,(8o), где 6Л - некоторые линейные операторы, и подставляя полученные решения в первое из вариационных уравнений (11), придем к системе г    Эф(’>0>    „ Э(Д°(8а))

J dv             dv

Для решения этой системы предварительно производится ее дискретизация, тип которой определяется выбором базиса в пространстве функций %. Обозначим вектор неизвестных, полученный в результате дискретизации, через 8а, вектор правой части -через 8J. Тогда система вариационных уравнений (13) приведется к следующему-набору систем линейных алгебраических уравнений:

[Д(,)]8а ^8J(0, которые в целом представляют собой переопределенную систему для неизвестных 8а;

• г)    после решения данной системы, например, по методу наименьших квадратов производится переход к очередному приближению по формуле:

• 2.    Двойственный метод последовательных приближений

• 3.    Вариационный метод

а(1,=о(0)+р8о№,                          (14)

где р - экспериментально подбираемый числовой параметр - длина шага. Процесс повторяется с новым значением проводимости о.

Данный метод отличается от предыдущего тем, что на этапе а) решаются не задачи Дирихле, а задачи Неймана с граничным условием (4). Кроме того, коррекция проводимости осуществляется из условия минимума невязки между вычисленными на этапе и найденными из эксперимента граничными значениями потенциалов. Ввиду очевидности преобразований приведенных в п. 1 формул, описание алгоритма опускаем; подчеркнем только, что при решении задач Неймана необходимо соблюдать обычные предосторожности для получения единственного решения.

Данный метод основан на утверждении о том, что задача Дирихле (1)-(2) эквивалентна задаче минимизации функционала

ЛШ = 7Г j-oVcpl^Q(15)

• ² и

• при ограничениях:

Vj = O,(16)

TIl=

хе 2,                          (18;

dv где j - вектор гоков внутри области j = oV(p.                                   (19)

Если теперь предположить, что проводимость о, наряду с потенциалом (р. является основной неизвестной, то, как уже отмечалось, необходимо иметь множество решений краевых задач для множества граничных условий, определяемых одной или несколькими независимыми переменными, которые могут изменяться непрерывно или принимать дискретное множестве значений.

Рассмотрим алгоритм решения данной задачи, получивший название метода переменных направлений, в англоязычной литературе - "alternating direction implicit method", сокращенно ADI:

• а)    задается распределение проводимости в нулевом приближении сг-=о" и строится решение 2N задач минимизации функционала (15) - N задач по аргументу / с ограничениями (16), (18)-(19) при i=l,2,...,N и N задач минимизации по аргументу тр с ограничениями (17) при /=1,2,...,/V.

Нетрудно видеть, что первая серия задач - до задачи Неймана для уравнения (I), вторая серия - это задачи Дирихле для того же уравнения;

• б)    просуммируем функционалы вида (15) по всем значениям индекса L Считая в получившемся функционале проводимость неизвестной, произведем минимизацию по данной переменной. После этого произведем коррекцию проводимости по формуле (14) и перейдем к этапу а) с уточненным значением проводимости с.

Идентификация параметров неоднородных материалов в линейно упругой области

Эта задача ставится и решается в точности так же, как и описанная в предыдущем н.п. модельная задача, со следующими заменами:

• •    проводимость материала заменяется цензором упругих модулей 'а- ⁴а(л). индекс «4» определяет раит данного тензора;

• •    место потенциала <р занимает поле перемещений и(х):

• •    закон Ома (19) заменяется законом Гука, при этом плотность тока заменяется тензором напряжений о, а градиент потенциала - тензором деформаций е;

• •    граничные условия типа Дирихле и Неймана будут иметь вид

и s-и,. o(»;-v v PL.

где и£ - заданные на границе перемещения, Рх - заданные на границе усилия.

После этого алгоритмы типа I) и 2) предыдущего н.п. будут содержать в точности те же этапы, что и алгоритмы доя решения модельной задачи. Для построения вариационного метода решения следует использовать следующий аналог функционала (15):

(с, £) = ^ J; О - Hi £ е dQ .                      (20 > si

Описание подробностей работы с функционалом (20) приведено в работе [9] и поэтому на них не останавливаемся и переходим к более интересным результатам. связанным с идентификацией свойств материалов с нелинейным поведением.

Идентификация параметров неоднородных материалов в нелинейно-упругой области

Начнем с вариационной формулировки основной рассматриваемой здесь задачи - об определении физико-механических параметров материала неразрушающими методами. Прежде всего, заметим, что аналогом функционалов (15) и (20) будет следующий функционал:

7_лг(о, е) = ^ ||а-Е(Е,х);²<Ш,                    (21)

где Е - тензорная функция тензорного аргумента, определяющая нелинейное поведение неоднородного материала.

Главной проблемой теперь является то, что в случае, когда относительно конструкции функции Е никакой информации нет, задача восстановления этой функции по результатам граничных измерений сводится к реконструкции оператора, реализующего отображение кинематических граничных данных в силовые или наоборот. Такая интерпретация обратных коэффициентных задач для рассмотренной выше модельной задачи была впервые дана Кальдероном и на этом пути были получены некоторые результаты о разрешимости и единственности.

Упростим задачу идентификации, предположив, что структура искомой функции Е задается конечным числом параметров A_t, А₂,.--> А,, являющихся функциями только пространственных задач. Тогда функционал (21) при фиксированных распределениях напряжений и деформаций будет зависеть только от этих параметров и мы приходим к классической задаче нелинейного программирования: найти минимум функционала: