Об определяющих соотношениях пластичности при циклическом непропорциональном нагружении

В течение последних 10-15 лет появились систематические исследования цикжческой пластичности металлов и сплавов при сложись нагружении. Мы тгриведем здесь краткое описание основных результатов экспериментов, изнестиых нам по публикациям (ск., например, работу И 1 и ае ссылки). Изучалось повеление тонкостенных трубчатых образцов. Fa крутильный и продольный управляющие механизмы испытательных машин подавались различные периодические воздействия с 'разностью и без разности фаз. Формы воздействий и их типичные характеристик показаны на Рис.1. Несколько видов циклов с различной формой траекторий о пространстве деформдргй А. А. Ильюшина показаны со Рис,2, а.Типичная сложная история деформирования, включающая различные 1@клы, показана на Рис.2,6. В Табл.1 представлены А,аннью о разлитых истользоь айны х материалах и температур?

\ 6pt«w

Сгорать д»*@жа8|мч “ 0.1 ИЛ.

7     \ f?wi

Рио Л. Форма и харЕктеристш® воздействий ис-лйтаний. Реакция испытываемых образцов оказалась довольно сложной и разнообразной. В целом можно отметить, т-ти величина максимального эффективного напряжения обычно стабилизируется в ходе циклпческоро нагружения, Этой стабилизащ™ всегда предшествует переходная стадия» которой может быть циклическое упрочнение при пропордйОЕг v1'м или непропорцион слоном нагружении (Рис.З.а), цикличе-. о разупрочнение [1} рлгь.цб) или поперечное упрочнение 11] (на Рис.З-.в - с коедедующим циклическим разупрочнением). -

Отмечено, что более сильное изотропное упрачненио при непротхрдиснаденом циклировании не монет быть объяснено с использованием простых мер деформации, таких как накоштонч шасттчческая деформация, наксгденная полная деформация за гыкя, максимальная эквивалентная деформаиж в течение пию® или работа Формоизменения. Сложность явления и его описания побудиж нас к изучению возможных физическш механизмов, которые могли бы его объяснить.

О возможном механизме доп о лнительного упрочнения

Сравнение поведения различных материалов было проведено с учетом трех физических параметров :

о гомологической температуры, Т._„._ /Т_„.вп . котовая мерой активности "''очечных дефектов в диффузионных

'40Л6Т ЯВЛЯТЬС И ГПрССаХ,

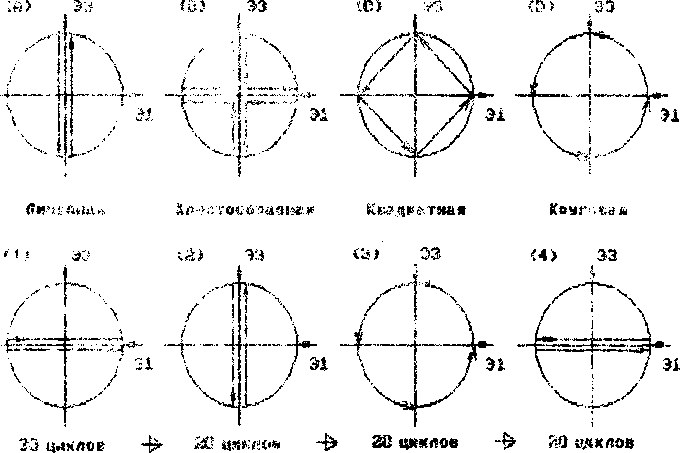
Рис.2, Форма циклических траекторий в пространстве деформаций А.А.Мльюиина. а)форма типичных циклических траекторий;

б? история деформирования.          *

• - пара метра угру гой анизотропии (21. -^-rs^r^-- 'O^.c^ и c^ - упругие постоянные материала), который контролирует энергию, высвобождаемую в ходе некоторых гм-локационных реакций

энергии дефекта упаковки (ЭЖ), измеряемой безразмерным комплексом ;-• а)Ь ( ^^^ - величина энергии дефекта упаковки, 3 mi.T.^JlB сдвига. Ъ - ветчина вектора Бюргерса ).

По нэаему мнению, процессы деформационного упрочтзния и разупрочнения при ’дтклщювании наиболее полно характеризует г;латии параметр. Вес материалы распределяются по трем группам В а''л-2) сопла'чо уровню ЭДУ. Металлы с высоким уровнем Э1У имели слабое дополнительное упрочнение. Металл со средним уровнем ЭДУ дополнительно упрочнялся в ходе нагружения по программе (з) (Рис.2,6), но любые последующие циклы внутри этой окружности, например (4), не изменяли его стабильного упрочненного состояния. Материалы с низким уровнем ЭДУ обнаруживали наибольшее дополнительное упрочнение, однако при последующих циклах (4) имело место циклическое разупрочнение, зависящее от истории нагружения. Мы ограничились рассмотрением металлов третьей группы, для которых интересующий нас эффект выражен наиболее ярко. Хиртом замечено [33, что в металлах и сплавах с низкой ЭДУ имеет место сильное барьерное упрочнение. Можно предположить, что эволюция формирования барьеров в этих материалах существенно зависит от взаимодействия систем

Материал	Кристал структура	Энергий рееекиа упаковки, эог/сн2	Размер зерна, МКН	Гемпература ютманий
ТВ45МЗ	оцк			%f
Щ	г»	200		20иС
№	гик	30		20°^
Си	гик	40	78	20°С
316	гик	20	40	20°С
304	гик	20	-	20°Сиб00°С
03Х21Н32 НЗб	гик	-		20°С

Уровень ЭДУ		Нажриа/!
высокий	~31й2 -5-Ю*3	МА металлы с ОЦХ крист. рееегкоС
срериий		Си
низкий	*3-10	^осенив нереабеюедих сталей, сплавь

ТаблЛ.Данные об использованных Табл.2.Три группы материалов с материалах и температуре         разным уровнем энергии испытаний.                         дефекта упаковки.

скольжения, которое, предположительно, более интенсивно пои сложном нагружении. Дополнительное упрочнение, возможно, ОбЪЯСНЯеТСЯ активностью большего количества действующих систем скольжения в каждом зерне поликристалла, подвергаемого непропорциональному циклированию. Это приводит к существенному

Smax (напряжение по Ми з есу), НПа

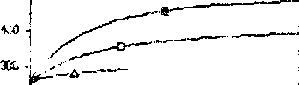
D ' №

■ - '/Л »{0)

О Ц---г---^----^...

О 25 Л ^ О

;Р (накопленная пластическая деформация)//.

Smax (н апряжение по Мизесу ),НПа

500 Рх^ юс .                 "

300 -

О) Лоо«*е»*те<м1еоть<3>^<4>, ^    дееовеацмонное ваав»чненае

„         пчеле иэдклой $3>

100 -

• о 4----,----,---------,----

• О 20 Ю «0       80

Циклы

Smax (напряжение по Мизесц),МПа ЙГО-.----------------------

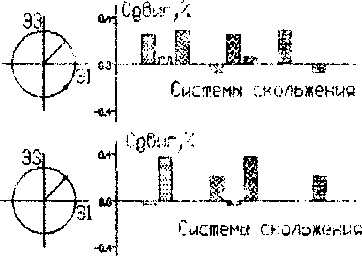
4ОЭ-

Гк>.Ж' эба^ънгсяи 1 >-Н2>

■ (2)

3ff»<« клеречногс уоротиунии

200          300

Циклы

ХО*

да ю Si

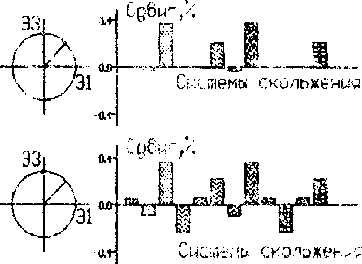
Рйс.З. Реакция образцов в ходе Рис.4. Активность систем экспериментов;                скольжения ГЦК-монокристалла эффект дополнительного упрочнения; в ходе несинфазного цикла эффект циклического разупрочнения; с моделирование). эффект поперечного упрочнения;

Плотность барьероб

33,

33,

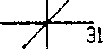
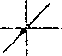
Системы скольжения

Плотность барьеров

Системы скольжения

Плотность барьеров

Плотность барьеров

Системы скольженья

Плотность барьеров

31 о

Wca—— „Мп -..__—..........

Системы скольжения

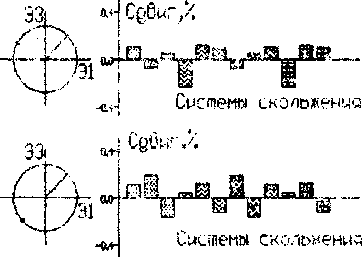
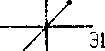
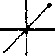
Рис.5.Процесс накопления плотности барьеров Ломер-Коттрелла в ходе синфазного цикла моделирование .

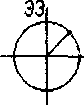
Плотность барьеров

Системы скольжения

(Плотность барьеров

оиИ_____щ_____S3_ей.__

Системы скольжения

[Плотность барьеров

Системы скольжения

Системы скольжения

Плотность барьеров

Системы скольжения

Плотность барьеров

Системы скольжения

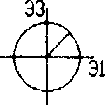
Рис.6.Процесс накопления плотности барьеров Ломер-Коттрелла в ходе несинфазного цикла моделирование .

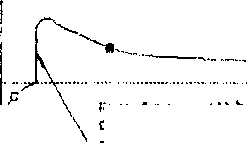
у » иатчеиию их взаимодействия. Сравнение результатов оценки плотности барьеров в течение пропорционального и копрепирдиочального (с разностью фаз 90°) циклов показывает ...... одопоцобность этого предположения. Динамика активности систем щктете чл~ ГЦК монокристалла в течение одного цикла нагружения показано но Рис.4. Для этого же кристалла на Рис.5 и Рис .6 показана динамика об терзания барьеров Ломер-Коттрелла за один цикл,. соответственно, пропорционального и непропорционального нагружения. Системы скольжения кристалла были взяты в соответствии с ориентацией стандартного тетраэдра Томпсона. Все системы скольжения распределены по четырем грушам (каждая группа включает три системы скольжения - см. Рис. 4-6; к сио-тетствии с принципиальной возможностью образовывав указанные барьеры. Дислокации систем сколыжэаия каждой группы могут образовывать барьеры Ломер-Коттре.лла друг с другом и не могут образовывать подобные барьеры с дислокациями других систем слежения. Динамика активности систем скольжения в -течение непропорционально! о цикла (Диагр. 2-6 на Рис.4) показывает болте обширную активность всех систем скольжения в сравнении с пропорциональным циклом (Диагр.1 на Рис.4).

Плотность барьеров может быть принята в качества ;:руктурного параметра, связанного с напряжением течения.

Определяющие уравне н ия при неп р опорциональном ци клическом нагружении

В отличие от часто используемого способа построения определяющих соотношений непосредственно в макропеременных мы считаем целесообразным применить здесь следующий прием, заключающийся в

• г) поиске объяснительного механизма явления на том ■системном уровне, где проявляется это явление и легче всего установить определяющую связь;

• з) осуществлении перехода от использованных переменных мезоуревня к макропеременны^, что позволяет получить замкнутую в терминах макропеременных систему определяющих уравнений.

Как уже было замечено выше, для описания дополнительного циклического упрочнения может быть введен скалярный параметр, имеющий физический смысл плотности дислокационных барьеров, В настоящей работе рассматриваются барьеры Ломер-Коттрелла. Эти барьеры могут образовываться взаимодействием дислокаций на каждой системе скольжения с дислокациями двух сопряженных систем скольжения. Эволюционное уравнение выводится в предположении однородного распределения дислокаций каждой системы скольжения по объему кристалла, что может иметь место на начальной стадии деформационного процесса. Эволюционное уравнение связывает скорость образования барьеров « со скоростью сдвига rccl на действующей системе скольжения и с плотностью подвижных дислокаций р'^’ на сопряженных системах скольжения ст - A pcorjl^actl. А = const, А > 0. cd

Плотность сидячих (неподвижных) дислокаций пропорциональна о-параметру. Принимая во внимание последнее предположение, может

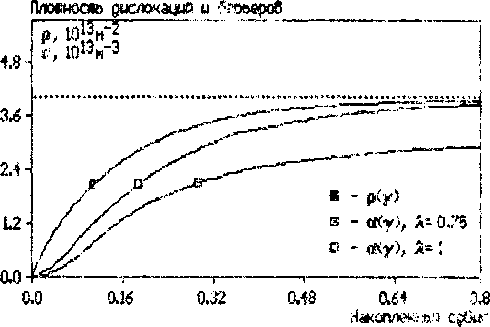
Рис.7, Рост параметров р и й, мо«елирнешй даашннити (2) и Ш.

быть записано следующее уравнение :

ст = (А рсог^ - В ст )!racl|, В = const. В > 0. саэ Используется эволюционное уравнение плотности дислокаций для случая циклической деформации (учитывающее аннигиляцию дислокаций) [41

р - (С - D Р )|y^OCti> С < D положительны"- константы С 3D

Был проведен анализ системы дифференциальных уравнений (2) и (3) при следующем условии рсоп,=хр, 0<х<1. Параметр х определяет стационарную точку « и, следовательно, при наличии большой плотности дислокаций на сопряженных системах скольжения, например, имеющем место при сложном нагружении, параметр « такки будет достигать большего стационарного значения. На Ряс.7 показан рост ри» три увеличении накопленной сдвиговой деформации.

Для произвольного деформированного состояния предложена континуальная модель. Согласно этой модели в каждый момент времени действующие плоскости скольжения совпадают с плоскостями главных сдвигов. Скорости сдвигов по шести ‘'псевдосистемам'' скольжения, связанные с этими плоскостями, определяются с помощью следующих соотношений :

г = Й.-В-П, 1-Г.Ъ.

С 4D

где D' - девиатор тензора скорости деформации. А. б - единичные векторы, определяющие 1-ю псевдосистему скольжения в базисе главных осей 5 (Рис.8). Тензор плотности дислокаций вводится следующим образом :

р

Р = -g-K .

где В - девиатор тензора деформации. B_v=(^3B^_cl)^lz~. k.i-ГГЗ. р - скалярный параметр, изменяющийся согласно (3) при \r^act’,= £ 1ь. I Величины плотностей дислокаций на сопряженных исевдосистемах подсчитываются следующим образом :

р. = Й. . Р^-б 1=Т7Б (активные псевдосистемы),   се>

J=1.2 (сопряженные псевдосистемы) , где ориентация векторов й^ и б . 3=1.2. относительно базиса, связанного с 1-й псевдосистемой, определяется как если бы эта 1-я псевдосистема была реальной системой скольжения ПЖ кристалла, а связанные с ней два - сопряженными.

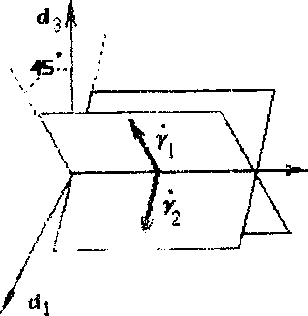
Рис.8. Две псевдосистемы скольжения в базисе главных осей тензора скоростей деформаций.

Предположено, что два скалярных параметра -аир с достаточной полнотой отслеживают деформационную историю. Связь между девиатором скорости деформации В и девиатором напряжений S может быть взята в следующей форме :

D

В =---C7D

Ф(р.а) где Ф - заданная функция упрочнения, D_u - интенсивность девиатора скорости деформации . D_u= (z/aD_kLD_{k t} )^1/z.   k,t=1T3.

Структуру функции Ф предложено взять в форме

Ф(р.а) = F + М р™ + N а",           C8D где F.M,N.m и п - материальные константы, определяемые из опытов на циклическое пропорциональное и непропорциональное нагружение.

Резуль та ты численного эксперимента

Моделировался рост параметров упрочнения при циклической деформации. Деформация задавалась функциями s = ^sln cot и г = =ra31n(cot-p). где £ и г - величины осевой и сдвиговой деформации, sa и ra - их амплитуды, выбираемые из условия постоянства максимальной эффективной деформации э^ при различных ra=V3cv t - время, со - круговая частота. Принимались следующие начальные условия: p(t=O)=1O11 м"2,  a(t=0)=0 м"э. значения материальных констант: А=20.0 м*1. В=20.0. 0=2.5-1014 м"2. В=6.0 и параметры нагружения: <о=0.2 с"1 и этах=0.5%. На Рис.9.а-б показан, соответственно, рост плотности дислокаций и барьеров против номера цикла. Зависимость стационарной величины а от фазового угла <р приводится на Рис.9.в.

Выводы

Выбран и обоснован физический механизм, приводящий к дополнительному изотропному упрочнению некоторых металлов. Обозначен определенный класс металлов и сплавов, для которых этот механизм, возможно, является определяющим. Взаимодействие систем скольжения, вызывающее образование сильных барьеров, может определять характерный размер постоянных линий скольжения в циклически деформируемых металлах. Построена замкнутая континуальная модель в терминах макропеременных в предположении определяющей роли барьерного упрочнения. Эта модель описывает эффект дополнительного упрочнения при циклическом многоосном нагружении с разностью фаз.

1ксе*хз» смслоищиЯ, Ю^и*-

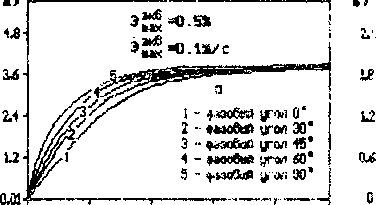
Плс®«хм> $4»еро6, Ю“м'5

.         3^-*.5Х э£5*л:*/с

- фЖМ>в<)Й угол 0' - fasotta угол 30" - «азобш угол 16* - оаообиа угол 60' - faooflWI угол Я"

О <         8        12        16      20       0         1         8        12        16      20

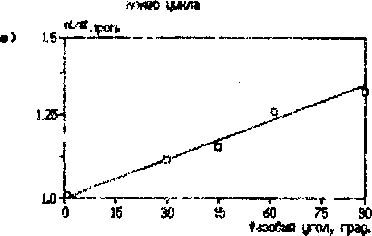
Рис.9. Рост параметров упрочнения при непропорциональном циклическом нэгрутемии; аз рост плотности дислокаций, б)рост плотности барьеров, нестационарное значение «.

Затс ратура

• 1.    Беналлал А- , Марки ,х , Определяющие уравнения утруговязкопластичности дая непропорционального циклического нагружения. Теор. осн. инж. расч. . 1988. моЗ. стр. 69-83.

• 2.    Набарро Ф. Р. Н. , Базинский 3- С. , Холт Д. Б. . чистых монокристаллов. М. • Металлургия, 1967, 214 с.

  Пластичность

  
  

• 3.    Hi гth J.P. On dislocation interaction

  n the FCC lattice.

  
  

  J. Appi. Phys. , 1961, v 32, Nc4, pp. 70U-706-

  • 4.    Essmann U. , Mughrabi H. , Annihlation of dislocations during tensile and cyclic deformation and limits of dislocation densities, Phil. Mag. A, 1979. V. 4, No6, pp 731~756-

• Пермский государственный технический университет