Об оптимальном управлении тепловым режимом зданий

В.И. Панферов, Е.Ю. Анисимова, А.Н. Нагорнаяг. Челябинск, ЮУрГУ

Рассмотрена задача оптимального управления тепловым режимом здания в нерабочее время. Найден алгоритм оптимального управления режимом прерывистого отопления. Разработан метод построения конкретных графиков подачи теплоты для выбранных зданий, оценена экономическая эффективность оптимального управления в условиях как централизованного, так и автономного теплоснабжения.

Известно, что в нежилых помещениях в нерабочее время температуру воздуха можно поддерживать на более низком уровне, чем в остальные промежутки времени. Это дает возможность сэкономить расход теплоты на отопление. Однако для получения максимального эффекта от реализации такого, так называемого режима прерывистого отопления необходимо решить задачу об оптимальном управлении этим режимом. Рассмотрим постановку этой задачи.

Как нами установлено [1, 2, 3], температурный режим помещения удовлетворительно может быть описан следующим дифференциальным уравнением

Т^ + О(т) = ^о(т), (1) ат где 6(т) - избыточная температура, 0(4) = tB (т) - tH (т), ^(т), tH(j) - соответственно температура внутреннего и наружного воздуха, Т - постоянная времени, И^ (т) - мощность системы отопления, т - время, к - коэффициент передачи.

Количество теплоты, израсходованной системой отопления, оценивается функционалом

/^(т)^, (2) о где тя - заданное время.

Задача оптимального управления тепловым режимом формулируется следующим образом [4]: требуется найти такое управление мощностью системы отопления % (т), которое переводило бы объект 0(ти) = 0^ управления (1) из заданного начального состояния 9(0) = 0_О в заданное конечное состояние 0(т и) = 0^ за заданное время т_я , при этом расход теплоты I системой отопления был бы минимальным. Формально это записывается так;

1 -> min ■

Мощность системы отопления должна при этом удовлетворять следующему ограничению:

<^0(т)<С“, (3) где И^отах- установленная мощность системы отопления, Ид™" - минимальная мощность системы отопления, как рекомендуется работой [5], эта мощность должна обеспечить поддержание температуры внутреннего воздуха на уровне 12 °C , исключающем выпадение конденсата на поверхностях ограждений.

В работе [6] формулировалась аналогичная задача оптимального управления, однако при решении этой задачи предполагалось, что температура внутренних поверхностей ограждений «...задана и сохраняет постоянное значение в период натопа». Заметим, что данное допущение, как это нетрудно видеть, означает, что ограждающие конструкции здания, отличающиеся наибольшей теплоемкостью из всех участников теплообмена, никак не влияют на решение поставленной задачи, т.е. на выбор оптимального управления. Далее в работе утверждается, что исходная условная задача сводится к некой безусловной задаче, экстремалями которой являются прямые линии, т.е. в оптимальном процессе ?5(т) должна быть линейной функцией времени. Затем авторы, полагая дополнительно, что во время натопа и температура наружного воздуха является константой, из модели процесса находят, что оптимальное управление -мощность системы отопления тоже должно быть константой. После этого в работе [6] делается совсем нелогичный вывод, что «...оптимальность управления означает минимальность времени» натопа помещения и авторы переходят к рассмотрению задачи о максимальном быстродействии. Конечно, можно продолжить рассмотрение всех особенностей указанной работы, однако в этом нет большого смысла: уже отмеченные замечания делают сомнительным обоснованность выводов, поэтому достаточно смело можно утверждать, сформулированная выше задача оптимального управления еще не решена

Кстати говоря, из выводов работы [6] следует, что оптимальное управление имеет только один интервал постоянства, кроме того, авторы, невидимому, не различают понятия времени натопа и времени максимального быстродействия. Время натопа (разогрева помещения) может значительно превышать время максимального быстродействия, время максимального быстродействия - это минимально возможное время, за которое можно «натопить» помещение до заданной температуры.

В работе [7] оценивается эффективность режима максимального быстродействия, причем одним из декларируемых авторами тезисов является утверждение о том, что «разогрев ...необходимо начинать с разогрева наиболее теплоемких частей помещения» Вместе с тем, как уже это отмечалось, при отыскании оптимального управления авторы в [6] полагали, что температура внутренних поверхностей ограждений «...задана и сохраняет постоянное значение в период натопа». Таким образом, наблюдается явное противоречие между допущениями, принятыми при решении задачи, и тем, что рекомендуется при практическом использовании, якобы, этого решения. В целом, создается впечатление, что авторы, поставив, но, в общем-то, так и не решив задачу (как следует из материалов работы [7], это они поняли и сами), либо позаимствовали то, что давно было известно, например, в металлургической теплотехнике из результатов задач оптимального управления нагревом металла, эти результаты были обобщены, в частности, в работах [8, 9], либо высказали свои интуитивные соображения.

Однако вернемся к рассмотрению поставленной задачи и подчеркнем, что для режима прерывистого отопления данная задача имеет следующую особенность: в начале и в конце рассматриваемого промежутка времени [0,тн] избыточная температура 0(т) должна быть равна одному и тому же значению 0О , такова особенность режима прерывистого отопления.

Для решения поставленной задачи нами была использована теорема об и интервалах в формулировке работы [10], согласно этой теореме оптимальное управление в данной задаче будет представляться кусочно-постоянной функцией, принимающей граничные значения и имеющей не более двух интервалов постоянства.

Для простоты будем считать, что т_н таково, что в графике % (т) есть два интервала постоянства и что длительность этих интервалов одинакова. Мощность системы отопления для первого интервала обозначим через И^, а для второго интер

вала - через 1Г02. Так как за время режима прерывистого отопления избыточная температура 0(т) должна измениться от значения 0О до значения 0О то на основании (1) получается следующее уравнение, связывающее 1Т0] и 1У02 :

^02+^01 Д1-п) = 0о(2-а), (4) где а = 1-ехр(-тя /(27)).

Функционал I преобразуется в обычную функцию двух переменных ^_0] и 1Т₀₂ и будет иметь вид:

/=^01 у+ 1^02 у-         (5)

Здесь общий множитель т„ /2 можно просто опустить, так как он не влияет на результаты решения задачи, т.е. на ответ.

Таким образом, поставленная задача оптимального управления свелась к условной задаче нелинейного программирования: требуется найти минимум функции I, заданной уравнением (5), при условии, что ее аргументы 1Д,] и Ищ должны удовлетворять соотношениям (3) и (4):

1 -> min

где G;

iiz^mm<  w w < W^y •

"0 - "01 ’ "02 - "0 > jW02 + W701 (1 - a) = 0O (2 - a).

Заметим, что исходную задачу неклассического вариационного исчисления можно свести к точно такой же задаче нелинейного программирования и другим способом, а именно методом параметризации функции управления, конкретно представляя ее состоящей из двух дискрет одинаковой длительности [И]. Для решения сведем условную задачу оптимизации (6) к безусловной методом подстановки, для этого из уравнения (4) выразим, например, И^ через W_ox и подставим в критерий (5), тогда будем иметь, что

/ = 0о^^ + ^о1 (7) к

Учитывая, что коэффициент а в реальных условиях удовлетворяет неравенству 1 > a > 0, из (7) найдем, что чем меньше мощность системы отопления на первом интервале постоянства, тем экономичнее режим, следовательно, на первом интервале мощность системы отопления должна быть равна f-l-g™. Примечательно, что если из (4)

выразим J^qj через W_m и подставим в критерий оптимальности, тогда задача оптимизации будет иметь вид:

7=0О

--^02

^(1 - а)

а

> min • »02

Из последнего соотношения следует: чем больше величина ^, тем меньше величина I, следовательно, на втором интервале мощность системы отопления должна быть равна Wq [12].

Таким образом, сначала для простоты решения задачи мы полагали, что длительность интервалов постоянства управления одинакова, однако на самом деле это далеко не всегда так, длительность интервалов постоянства в общем случае должна быть различной. Теперь выясним, какой должна быть длительность каждого интервала, с тем чтобы в начале и в конце процесса температура была бы равна 90 . Решение задачи оптимального управления в такой постановке, вероятнее всего, даст больший эффект. Обозначим длительность первого интервала через Т], а второго - через т2 Очевидно, что величины связаны следующими соотношениями

Ж₀₂ 1-е ^Т +кЖ_т е^т — 1 +a

' I . А )

.^l +^2 = т„>

= а60;

° (9)

где 1Т01 = 1Ротт - минимальная мощность системы отопления, 1PO2 = И^™3"4 - максимальная, установ ленная тепловая мощность, а = 1 - ехр--. ( Т)

Найдем из первого уравнения системы (9) вы ражение для определения т2

Из второго уравнения системы (9) найдем, что продолжительность первого интервала времени будет определяться следующим образом:

(И)

Функционал I в этом случае будет иметь вид

Понятно, что весьма интересен вопрос о том, будет ли справедливым в данном случае установленный при предыдущем допущении результат: чем меньше W_ox и чем больше ^₀₂, тем лучше, тем экономичнее режим натопа. Ответить на этот вопрос можно, если, во-первых, выяснить, имеют ли поверхности (F_O1,1F_O2,7) достаточно типичный вид и, во-вторых, вид этих поверхностей такой, что позволяет ответить на поставленный вопрос.

С этой целью, используя выражение (12), построили зависимость критерия I от мощности системы отопления на первом и втором промежутках времени. Эта поверхность приведена на рис. 1.

Рис. 1. Изменение критерия I при различных значениях тепловых мощностей системы отопления на первом и втором временных промежутках (в режиме прерывистого отопления)

На рис. 2, 3 приведены сечения этой поверхности плоскостями Ж01 = const, и J702 = const. Поверхность строилась для области, Вт

Г0<^₀₁<1200    1

[3000 < Ж02 < 4236] '

Это обуславливается теплотехническими характеристиками следующего здания. Здание удовлетворяет требованиям второго этапа энергосбережения для города Челябинска. Мощность системы отопления 4236 Вт. Площадь стен дома

F_Cm ⁼ 79,27 м²; площадь перекрытия F_n =69,12м². Коэффициент теплопередачи окон К_ок = 0,6 Вт/(м² °C), общая площадь окон F_0K = 11,55 м². Наружные двери площадью F_d6 = 2,6 м² ; коэффициент теплопередачи дверей К_дв = 1,05 Вт/(м² °C). Температура наружного воздуха t_H = -34°С; начальная температура воздуха в помещениях здания равна 21 °C.

54000 г 52000 £ 50000 - 48000

W2, Вт

—♦—l=f(W2), W1=0Bt —•—l=f(W2) при W1=500Bt -*-l=f(W2), W1=1000Bt

Рис. 2. Зависимость критерия I от различных значений максимальной мощности Ч'щ , и постоянной минимальной мощности И^ = 0 Вт (500 Вт, 1000 Вт)

48000 т 47000 £ 46000 - 45000

осмть-осчхгг^Фсм'Гсот-^'Т ООСОтГСОт-О^-ЮчТСМОООЬ-Ю СМ1П0О'г-'ТСОО><М1Л0О-г-СО<ОО>

W^ Вт l=f(W1), W2=3000 Вт -1- l=f(W1), W2=3500 Вт -^- l=f(W1), W2=4236 Вт

Рис. 3. Зависимость критерия I от различных значений минимальной мощности W^ и постоянной максимальной мощности W₀₂ = 3000 Вт (3500 Вт, 4236 Вт)

Стены здания выполнены из ячеистых блоков 5 = 0,75 м, с = 0,84 кДж/(кг°С); р=1000кг/м³; ^ = 0,31 Вт/(м°С). Постоянная времени Т = 54 ч . Из рис. 1 видно, что функционал, I, оценивающий количество теплоты, израсходованной системой отопления, имеет наименьшие значения в области, когда тепловая мощность на первом промежутке времени минимальна, а на втором - максимальна. Такой же результат подтверждается сечениями поверхности критерия I. На рис. 2 приведены три сечения критерия I при И^, =0 Вт. На рис. 3 приведено три сечения функционала I при ^₀₂ =3000 Вт, )Т₀2 =3500 Вт, ^₀2=4236 Вт.

По вышеизложенному методу был спроектирован оптимальный режим прерывистого отопления для ранее рассмотренного здания [13, 14].

На рис. 4 и 5 приведены зависимости продолжительности времени отключения и включения системы отопления и температуры внутреннего воздуха для различных параметров наружного воздуха; продолжительность нерабочего времени составляет 15 часов - с 18м до 900, что характерно для общественных зданий.

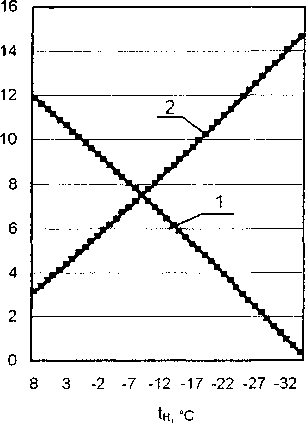
Рис. 4. Продолжительность времени отключения (кривая 1) и включения (кривая 2) системы отопления 4

В течение периода времени Т] мощность системы отопления снижается в данном случае до И/01 =0 Вт, а затем в течение периода т2 происходит разогрев (натоп) здания с максимальной мощностью системы отопления равной расчетной. Как видно из рис. 5, температура внутреннего воздуха не опускается ниже 12 °C, что согласуется с нормами [15].

Рис. 6 и 7 иллюстрируют случай, когда заданное здание подключено к тепловым сетям и производится качественное центральное регулирование отпуска тепла на источнике, т.е. мощность, необходимая для разогрева здания, является функцией температуры наружного воздуха.

Из рис. 6 и 7 видно, что при качественном регулировании, рассчитанном конкретно для данного здания, применять прерывистое отопление нецелесообразно. Это объясняется тем, что для нато-па, следующего за периодом отключения, нет резерва тепловой мощности, теплота, поставляемая тепловыми сетями практически полностью расходуется на компенсацию теплопотерь. Применение режима прерывистого отопления при централизованном теплоснабжении возможно в следующих случаях:

• 1)    если здание более «теплое», т.е. имеет повышенные коэффициенты сопротивления теплопередаче ограждающих конструкций, по сравнению с типовыми зданиями. В этом случае появляется некоторый резерв тепловой мощности, необходимый для осуществления натопа здания;

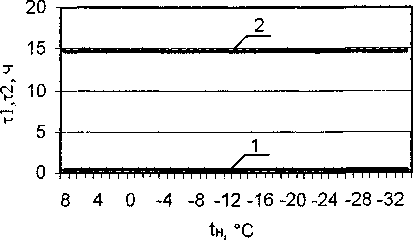
Рис. 6. Продолжительность времени отключения (кривая 1) и включения (кривая 2) системы отопления

tH,°C

Рис. 5. Значения фактической (кривая 1) и допустимой (кривая 2) температур внутреннего воздуха

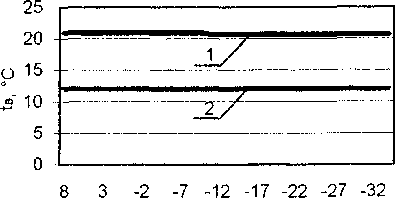
1н, °C

Рис. 7. Значения фактической (кривая 1) и допустимой (кривая 2) температур внутреннего воздуха

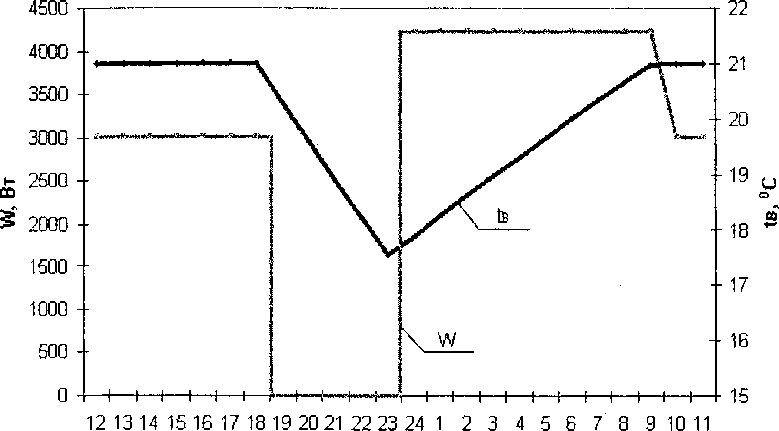
Время суток, ч

Рис. 8. Изменение мощности системы отопления и температуры внутреннего воздуха при оптимальном управлении

• 2)    если есть возможность отказаться от смешения теплоносителей в период разогрева здания. Это не противоречит санитарно-гигиеническим требованиям, предъявляемым к температуре поверхности отопительных приборов, так как натоп здания происходит в нерабочее время.

Выяснили, какой режим является более экономичным: режим прерывистого отопления или режим централизованного теплоснабжения при качественном регулировании на источнике [13, 14]. Для этого нашли количество теплоты, израсходованное системой отопления за нерабочий период времени из уравнения (2).

Расчеты проводились для указанного здания при температуре наружного воздуха минус 18°С.

Для режима прерывистого отопления из рис. 4 видно, что продолжительность отключения системы отопления составляет 5,04 часа, тогда, как это следует из того же рисунка, продолжительность натопа здания при мощности 1Ротах =4236 Вт равна 9,96 часа. График оптимального управления отоплением приведен на рис. 8. Расход теплоты за нерабочее время при оптимальном прерывистом режиме отопления определяется по формуле (2) и составляет: .

• 1    = 0 • 5,04 + 4236 • 9,96 = 42190,56 Вт-ч.

Если бы здание отапливалось по обычному качественному графику при тепловой мощности W_Q =3004 Вт, то расход теплоты был бы равен:

/ = 3004-15 = 45060 Вт ч.

Следовательно, в режиме прерывистого отопления достигается экономия теплоты 2870 Вт ч, что составляет 6,4 %.