Об оптимальных кубатурных формулах на анизотропных пространствах Соболева

Постановка и основные результаты теории кубатурных формул как нового направления математики принадлежат академику С.Л. Соболеву [7], предложившему функциональноаналитический метод для семейства подынтегральных элементов гильбертова пространства. Опубликованные им работы послужили источником интенсивного развития современной теории дифференциальных уравнений с частными производными и функционального анализа, новых направлений уравнений математической физики и вычислительной математики.

При больших численных расчетах возникает трудность в оптимизации процесса приближенного вычисления многомерных интегралов. Проблема заключается в том, что сама теория приближений функций в многомерном случае до сих пор не создала универсальные методы оптимизации кубатурных формул на классах функций, поэтому исследования задач теории ведутся с точки зрения разных научных направлений. Одним из таких направлений является функционально-аналитический подход, связанный с исследованием оценок погрешностей в классах суммируемых функций и линейных нормированных пространствах, включающих в себя интегрируемые функции.

Основные результаты исследования задач оптимизации кубатурных формул на классах функций анизотропных пространств, неодинаковых вдоль разных координатных направлений из-за дифференциальных свойств функций, рассматривались в работах Н.С. Бахвалова [1], С.М. Никольского [5], Ц.Б. Шойнжурова [8], М.Д. Рамазанова [6].

В частности, М.Д. Рамазанов исследовал кубатурные формулы на произвольном, но не весовом пространстве периодических функций с единичным кубом в качестве основного периода. Однако при таком определении нормы функции возникали определенные трудности при периодическом продолжении функции на единичный куб.

Ц.Б. Шойнжуров продолжил функции из рассматриваемой области на все пространство, «избавившись» от ограничений. Это позволило ему к периодической на всем пространстве функции применить преобразование Фурье.

Цель исследования - разработка алгоритмов построения решетчатых кубатурных формул, асимптотически оптимальных относительно интегрируемых функций, зависящих от ее дифференциальных свойств.

Методы исследования . Для достижения поставленной цели применяются методы, заложившие основу теории кубатурной формулы, а именно теоретические методы вещественного и функционального анализа, уравнений математической физики, дифференциальных уравнений с частными производными, численные методы.

Предварительные сведения и обозначения

В данной работе исследуются кубатурные формулы на классах функций анизотропного пространства W m ( E n ) с естественной нормой при 1 <  p < да :

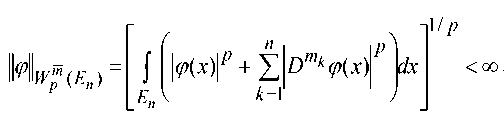
1/ p

n

J ^ ( x )| p + Е D m^k T (x ) Р dx

। ^ w m ( E_n )

E n k          k = 1             V

<да .

Известно [2], что дифференциальные свойства анизотропного пространства неодинаковы по разным направлениям, при 1 <  p < да оно является полным, оно сепарабельно при 1 <  p < да и при 1 <  p < да рефлексивно и равномерно выпукло.

Пусть k = 1,.., n , h_k >  0 - шаги решетки, x k - узлы формулы, N k - количество узлов решетки, C _k - коэффициенты формулы, m k - гладкость функции вдоль выбранных координатных направлений, m = ( m 1 m 2 ,..., m_n ) , Nⁿ = NN 2 ••• N_n - количество узлов формулы, f ⁿ ,^

m = n jm-1 I , h = diag(h1,h2,..,hn)  - матрица периодов,  Ah = {x e En, 0 < xk < hk ,

/ k k=1 k V k = 1,2,.., n} - фундаментальный параллелепипед с длинами ребер hk , Ah = hn = det h ^ 0 , A = {x e En, 0 < xk < 1, k = 1,2,.., n} - фундаментальный единичный куб.

Общее представление функционала погрешности и экстремальной функции. При оценке качества той или иной кубатурной формулы предпочтительней считается та, функционал погрешности которой имеет меньшую норму. Для отыскания нормы функционала погрешности в соответствующем пространстве используется экстремальная функция, которая является обобщенным решением некоторых дифференциальных уравнений в частных производных. Дифференциальный оператор l ( d ) = jr ( - 1 ) m k d ^{2 m} k , входящий в такое уравне- k = 0

ние, порождается видом нормы функции в основном пространстве.

Известно [3], что фундаментальное решение £ 2 m ( X ) оператора L ( D ) , вообще говоря, не единственно; оно определяется с точностью до слагаемого £ 2m ( x ), являющегося произволь-

ным решением

однородного уравнения   L(D)e°0 m = 0. Для того чтобы  функция

( ^

£2m (x) е Wp (En ) , удовлетворяющая уравнению I Е(— 1)m D   I^ (x) = 5(x), была фун- m      p    n                                 V to          J 0m даментальным решением уравнения

£ ( - 1) ^m k D ² m k u ( X ) = l ( X ),   l g W m* ,                            (1)

k = 0

необходимо и достаточно, чтобы ее преобразование Фурье удовлетворяло уравнению

L (2^/^)F £ m(x)]=1, nn где L(2ni^)= ^(- 1)”k(2ni^k)2mk +1 = 1 +'E(2n£k)2mk .

k = 1                                 k = 1

Как следует из теории преобразования Фурье, функция £2m (X) выражается через ее преобразование Фурье с помощью оператора обратного преобразования Фурье F 1: £2m (x) = F-1 [F[£2m (x)]] = F F-1 [£2m (x)]].

В нашем случае применительно к оператору L ( D ) , используя обратное преобразование

Фурье, находимо фундаментальное решение уравнения (1) в виде:

- 2 n i § x

^£ 2 m ^{( x} ) = J —-------------------- d ^ .                           (2)

En Е(-1)mk (2ni^)2mk + 1

k = 1

Фундаментальное решение оператора L(D) , порожденного видом нормы функции из основного пространства, будет иметь вид:

, Г f n ,    .

² m k

J

£ 2 m ( x ) = F ^{- 1} 1/ X ( - 1 ) ”'^k |2 n?k|

_  I k = 0

Ядро £2m(x) представляет собой бесконечно дифференцируемую при х^ 0 и суммируемую на всем пространстве функцию. Знаменатель выражения под знаком обратного преобразования Фурье (2) следует из формулы преобразования Фурье обобщенной производной

n

F ^{- 1} [ £ 2 m ] = Z ( 2 n - # ) ² m^k F [ £ 2 m ] + 1 .

k = 1

Приводимые ниже оценки для нее и ее производных с различными значениями гладкости функции m по координатным направлениям взяты из известных источников [4, 5]:

S 2m ⁽x) ^ ^C S ”

I 12m

I xl V

- kx e ,

\-1

, Ц <  1;

J

Ix J >  1, k >  0,

где C _m является непрерывной функцией от параметра m .

Для производных порядка 5 от функции £ 2 m ( X ) имеют место следующие оценки:

D^S£ 2 „ ( х ) <  C ^

(

I ^x l

V

,   ( ” 1 + m_k  .

² m k Z ₃ k ^{— 1}

V k = 1 ^{2 m} k

Л—1

J

,    Z n 1 + s k — 1 > 0, l x |< 1;

k = 1 ^{2 m} k

—kx e ,

| х |> 1, k >  0, 5 = ( 5 1 , 5 2 ,--, s n )■

Благодаря введению Ц.Б. Шойнжуровым [9] специальной нормы, для которой соответствующий дифференциальный оператор был хорошо изучен и описан в литературе, в частности, в работе [5] стало возможным применять свойства его фундаментального решения для нахождения экстремальных функций и норм функционалов погрешности кубатурных формул. Ниже применен сходный прием нормирования анизотропного пространства, и на этом пути получен ряд самостоятельных результатов.

ⁿ 1

Теорема 1. Пусть Q — ограниченная область в Еп , p — Z--> 0, l(x) - произвольный k=1 mk финитный функционал общего вида из пространства финитных функционалов из S* с Wm .

Тогда существует функция V0(x) = £2m (x) * l (x) e W™, являющаяся единственным решени- ем уравнения

г ⁿ .   .             ^

L ( D Ы x ) = Z ( - 1 ) m k D ² m k

V 0 ^{( x} ) = ^{l ( x} ) ,

V k = 1

J

где функционал погрешности общего вида имеет представление

^{11 ( x} ), V ^{( x} )) = J ⁽ D^m k ^£ 2m _k ^{( x} ) * ^{l ( x} ) ) D^m k V ^{( x} ) ^dx , V v ( x ) e W p¹ ( E n ) .

E n

Теорема 2. Если 1 < p < ^, p — Z — > 0, — + —; = 1, l (x) e W^*, £2m (x)* l(x) e Wm , то k=1 mk     p p            p                  p экстремальная функция ^l(x), соответствующая функционалу погрешности l(x), определяется равенством

n

Vl(x) = Z Dmk £ 2m (x) * Dmk £ 2m (x) *l (x) p-1 sgn Dmk £ 2m (x) *l (x), k=0

нормы функционала погрешности l ( x ) и экстремальной функции V i ⁽ x ) соответственно имеют представления

II ^{l ( x} )ll ^ ^m * =

Wp

II ^V l\w^m

Wp

n

J D

E n

.^{2 m} k

-I1/ p'

.                      p*.

£ 2 m ( х ) * l ( х )   dx

p'

J Z D ^m k £ 2m ( X ) * l ( x ) dx

-1/ p

.

E k = 0 n

,

Возникшая трудность, характерная для анизотропного пространства, когда все функции должны быть периодически продолженными с одним и тем же основным периодом, требовала, чтобы норма не возрастала при вычитании из функции ее нулевого коэффициента в соответствующих рядах Фурье. Для разрешения упомянутой проблемы в работе [10] был установлен критерий асимптотической оптимальности кубатурной формулы по коэффициентам, а именно порядок сходимости должен согласовываться с шагом решетки и гладкостью функции вдоль выбранных координатных направлений системой соотношений:

h m = h m 2 = ... = h m n = h m

Это дало возможность для усовершенствованных формул установить порядковую оптимальность на всем классе решетчатых кубатурных формул в анизотропном пространстве и найти из (3) зависимость шага решетки от гладкости функции по выбранному направлению, определенную равенством h k = h m / ^m k , N k = N m / ^m k , k = 1,2,..., n .

Построение элементарных функционалов погрешностей на плоскости с заменой узлов на другие с коэффициентами при значениях функции и ее производных. Разработка алгоритмов построения решетчатых кубатурных формул, асимптотически оптимальных относительно интегрируемых функций всецело зависит от нормы функционала погрешности в сопряженном пространстве. Особенностью анизотропного пространства является то, что в узлах решетки кубатурной формулы коэффициенты определены с учетом дифференциальной природы подынтегральной функции по выбранным координатным направлениям. Функционал погрешности кубатурной формулы внутри произвольной гладкой области Q анизотропного пространства будет минимальным, если использовать коэффициенты, определяемые из равенства

N

Z C _r Y . =

Y k = 0   ^Y k

^{1 -}^ k ^h k ^a k + ¹

a k = 0,1,...,m k ,

при любом значении порядка Pk старшей производной, гладкости функции m^ вдоль вы бранной координатной оси OXk, k = 1,2,..., n.

Переменными параметрами кубатурной формулы являются не только коэффициенты, но и узлы. Распределение узлов внутри области Q, учитывающей свойства анизотропного пространства, может быть произвольным. Тем не менее результаты работы относятся к формулам с параллелепипедальной решеткой узлов. В этом случае узлы формулы нумеруются с помощью мультииндекса / = (Д,/2,...,вп) с целочисленными координатами. Любой из них можно найти по формуле Xk = hk/k, где положительный параметр hk называется шагом решетки в k-ном направлении. В этом случае кубатурную формулу будем называть решетчатой.

Пример. Используя построенную формулу, вычислить интеграл jj ( x ^ + x 2 ) dxdy с 00

проверкой качества методов с известным решением.

Из формулы (4) найдем оптимальные коэффициенты элементарной квадратурной формулы на плоскости, когда функционал погрешности ортогонален многочлену степени m 1 =1 по переменной х 1 и ортогонален многочлену степени m 2 =2 по переменной х 2 :

r = p(1)_r(2) = 1A

00     0   0

r = r(*)c(2) = 1|_ 1

02     0   2    21

— . с = r⁽¹⁾c⁽²⁾ = ¹²

24        ⁰¹    2 3

3’

—

¹   |.  _r  -r(¹)r(2)-!A

I’  С1 о — С1 Со —

24 )    ^{10   10}    2 12

24’

С 11

= С ( ¹⁾ С ( ²⁾ =

2 3

3’

c С 12

= С

(1)   (2)

1 С 2

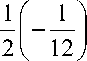
Вычисленные коэффициенты подставим в решетчатые кубатурные формулы, асимптотически оптимальные относительно интегрируемых функций, зависящих от гладкости по на- правлениям:

1 1

jj ^ ( X 1 , x 2 ) dx 1 dx 2 « С 00 ^ (0,0) + С 0M 0,1) + С 02 ^ (0,2) +

+ С₁₀ ф (1,0) + С_п ф (1,1) + С₁₂ ф (1,2);

5           1          (1

JJ Ф ^(x 1 , x 2 ) ^dx 1 ^dx 2 ~ —_Ф ^(0,0) + - ф ^(0,1) +1 —— 1 _Ф ^(0,2) +

00                24        3

+ ^ _Ф (1,0) + 1 ф (1,1) + (- ^ J ^ (1,2).

Подставим в полученную формулу значения функции в выбранных узлах

_Ф ( Х 1 + x 2 ) = _Ф (0,0) = 0, _Ф ( Х 1 + x 2 ) = ^ (0,1) = 1, ф (Х1 + x 2 ) = ф (0,2) = 4 и вычислим интеграл:

5^1,   (

JJ С ( x b x 2 ) ^dx 1 ^dx 2 ~7Т" ⁰ + 7’ 1 +1-Й7 I" ^{4 +}

00                 ²⁴     3 V ²⁴ )

+ — "1 +1" 2 + (—-L 5 = 5 « 0,8333333.(6)

24    3    V 24)6

Полученный результат подтверждает тот факт, что построенная элементарная куба-турная формула точно интегрирует многочлен первой степени по переменной х 1 и многочлен второй степени по переменной х 2 и совпадает с аналитическим вычислением интеграла.

Известно [7], что выбор коэффициентов при данных узлах представляет собой линейную задачу, а выбор узлов является задачей значительно более трудной. В данном пункте построены элементарные функционалы погрешностей на плоскости с помощью замены одних узлов решетки на другие, в которых вычисленные коэффициенты при значениях функции и ее производных минимизируют норму функционала. В заменяемых узлах решетки достаточно иметь только вычисленные коэффициенты при значениях функции в зависимости от гладкости выбранного направления. Заменять будем узлы решетки, которые не входят в область фундаментального параллелепипеда, с длинами ребер h 1 , h 2 на узлы, принадлежащие области, в которых вычислены коэффициенты не только при значениях функции, но и ее производных с учетом дифференциальной природы подынтегральной функции по выбранным координатным направлениям. Выбираем для замены такие узлы, чтобы погрешность как разность между неизвестным точным значением интеграла и приближающей его кубатурной суммой

(l, ^ = J ф ( x ) dx - 2_ Су ф ( 7 )

A         Y=1, N была равна нулю. Иными словами, должны так заменить узлы решетки формулы, чтобы функционал погрешности был бы ортогонален многочлену степени m1 по переменной х1, и многочлену степени m2 по переменной х2. При этом число заменяемых узлов N должно совпадать с числом одночленов M формулы, определяемым равенством

(a

M = min {«1, m 2}  + 2.(7)

V mk

Пусть функционал погрешности точно интегрирует многочлен первой степени по переменной х1, и многочлен второй степени по переменной х2. Количество одночленов M = (min{1,2})2 + 2 = 3 находим из равенства (7). Следовательно, число заменяемых узлов равно 3. Действительно, так как узлы Ф(0,1), Ф(1,1), Ф(1,2) выходят за область фундаментального прямоугольника, то они должны быть заменены внутри заданной области на другие узлы, в которых вычислены коэффициенты при значениях функции и/или при значениях производных:

_Ф (0,2) = _Ф (0,1), _Ф (1,1) = ^g, _Ф (1,2) = _{Ф (}⁽_о°0 .

Тогда, заменив в кубатурной формуле (5) вышеперечисленные узлы, получим:

—^ ⁽ 0 ^,0) + - ^ (0,1) + f^-

род) +

j j ^ ( Х д + x 2 ) dx i dx 2

+ 5 Ф (^1,0) + ¹ <°) +(-¹ № = 5 = ^0,8333333. (8)

Проверим качество построенной формулы, сравнив результат с известным аналитическим решением. Полученные одинаковые результаты аналитического мнения и в формулах (6) и (8) показывают, что с применением методов компьютерной алгебры усовершенствованы ранее полученные в работе [10] алгоритмы вычисления интегралов. Новизна метода проявилась в том, что в данном случае выбраны узлы решетки при фиксированных коэффициентах и эта задача, по словам С.Л. Соболева, «…является значительно более трудной задачей» и для классов функций, зависящих от гладкостей по выбранным координатным осям, построенные формулы сохраняют полученный ранее порядок сходимости.

Вывод

Преимущество кубатурных формул в анизотропных пространствах, характеризуемых решетчатым расположением узлов и постоянством коэффициентов для внутренних узлов, отстоящих от границы на расстояние порядка шага решетки, заключается в том, что учет гладкости функции вдоль выбранных координатных направлений дает более точные результаты, чем кубатурные формулы, где гладкость по всем направлениям одинакова. Получено общее представление о функционале погрешности и экстремальной функции, построен элементарный функционал погрешности на плоскости с узлами, лежащими внутри или же на границе произвольной гладкой области, который учитывает свойства пространства, сопряженного к анизотропному. Новизна метода проявилась в том, что для классов функций анизотропного пространства построены элементарные функционалы погрешностей на плоскости с помощью замены одних узлов решетки на другие, в которых вычисленные коэффициенты при значениях функции и ее производных минимизируют норму функционала. В заменяемых узлах решетки, которые не входят в область фундаментального параллелепипеда, достаточно иметь только вычисленные коэффициенты при значениях функции с учетом дифференциальной природы подынтегральной функции по выбранным координатным направлениям так, чтобы минимизировать норму функционала. С применением методов компьютерной алгебры усовершенствован алгоритм расчета интегралов. Рассчитаны коэффициенты оптимальных кубатурных формул в анизотропных пространствах Соболева. Качества полученных методов проверены на контрольных задачах с известными решениями. Результаты исследования апробированы на международной конференции «Дифференциальные уравнения и математическое моделирование», посвященной 70-летию со дня рождения профессора В.Н. Врагова (г. Улан-Удэ - оз. Байкал, 20 - 27 июня 2015 г.).