Об особенностях долговременной работы стыков изгибаемых элементов

В статье ставится проблема влияния фактора времени на работу строительных конструкций. В элементах конструкций при действии неизменной нагрузки продолжается нарастание деформаций. Авторы рассматривают ползучесть стыковых соединений изгибаемых элементов при действии неизменных во времени изгибающих моментов.

О влиянии фактора времени на работу строительных конструкций известно давно. Накопилось много фактов, подтверждающих, что в элементах конструкций при действии неизменной нагрузки продолжается нарастание деформаций. Например, увеличивается прогиб балок. Здесь проявляют себя различные процессы, протекающие во времени. Среди них первостепенную роль играет ползучесть. Говоря об изгибаемых элементах, необходимо учитывать, что все сказанное в значительной мере относится к их стыкам.

Рассмотрим ползучесть стыковых соединений изгибаемых элементов при действии неизменных во времени изгибающих моментов. Начало отсчета времени / совпадает с началом действия нагрузки. Имеется в виду, что стык перекрыт двумя одинаковыми накладками, на каждую из которых приходится изгибающий момент М. Предполагается, что деформациями накладок и соединяемых частей конструктивного элемента по сравнению с деформациями связей стыка можно пренебречь. Расчет ведется для двух типов связей: дискретно-сосредоточенных и равномерно распределенных по взаимно прилегающим поверхностям.

Дискретно-сосредоточенные кточеныё^ связи. К ним относятся соединения на болтах, заклепках, гелях, гвоздях и т. п. Геометрический центр их расположения служит центром взаимного поворота накладки и скрепленной с нею части элемента. Длину радиус-вектора, соединяющего центр поворота с Лй связью, обозначаем г.. Сдвиги связей и, соответственно, воспринимаемые ими усилия перпендикулярны к названным радиус-векторам. Если первоначальный (соответствующий т = 0) угол взаимного поворота И⁷,, _то сдвиг Ш_е г-й связи определяется как Ui_Q = r.W_Q, а придаваемое ею усилие будет равно Ni₀ = crU^. В последнем выражении величина с характеризует жесткость связи, которую считаем для всех связей одинаковой.

Условие равновесия накладки имеет вид равенства А4 = £ Ni_or, или, с учетом записанного выражения Ni₀:

Al = W.c^r².              (1)

Суммирование производится по всем связям, передающим нагрузку. Сумма X ^ представляет собой полярный момент инерции единичных площадей, расположенных там, где находятся связи. Обозначив его J , т. е. пользуясь формулой

равенство (1) переписываем в виде:

М * Wncl .

о Р

Отсюда

W.-^.             (3)

Подставив это выражение начального угла поворота в ранее написанные формулы начальных сдвигов и усилий, будем иметь;

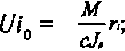
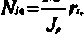
Исходя из предпосылок линейной теории ползучести для сдвигов t-й связи в момент времени t записываем формулу:

№0(/) = (//0+ -р^^-    (6)

с о

Здесь К (г) — ядро ползучести; N. (г) — усилие, приходящееся на i-ю связь в момент времени т.

Если в момент времени / угол поворота равен W (О, то U. (О = rW (0. Ранее было записано равенство U._o = г ^. С учетом этих выражений формула (6) принимает вид:

г^(0 = г^-[ к (т )М (т )Д.   (7)

с о

Умножив обе части этого равенства на г. и произведя суммирование по всем связям, получим:               ,

^(0 £ г² = fP₀£ r/+-f к (т )£ N. (т >]ft .

<                    с о

Но У г? = J?, y_N (Ar, - М, поэтому

^(;)-^ц+К|^(т)Л си> о или, имея в виду (3):

1Г(0= Wo 1+|^(т)Д . . о

{8)

Таково уравнение ползучести стыкового соединения с дискретными связями.

Дифференцируя (7) по I, будем иметь:

_г ^Й = 1 к (0^(0- dt С

Согласно (8) ^ ^ = Wk (t).

at v

Подставив это выражение в предыдущее равенство, получаем:

W (0 = -* (0^(0, откуда:         с cr,W0 = N, to.

Поскольку crW^ = N_i0, получаем равенство:

N, (О = N._Q.              (9)

Таким образом, усилия, действующие на связи, во времени неизменны.

Однородные равномерно распределенные связи. Типичным примером являются клеевые соединения. Решая задачу для этого вида соединений, там, где это уместно, будем пользоваться теми же обозначениями, что и ранее.

В точке, находящейся на расстоянии гот центра поворота, выделяем элементарную площадку dA. Перемещение центра этой площадки перпендикулярно к радиус-вектору, соединяющему с центром поворота, и в начальный момент времени (момент приложения нагрузки) равно U^ = rW_Q. Элементарное сдвигающее усилие, приходящееся на площадку, равно dN₀ = S_ocM и также перпендикулярно к названному радиус-вектору. Через S_o обозначена интенсивность сдвигающей нагрузки в центре элементарной площадки. Предполагается линейная зависимость между этими нагрузками и сдвигами, что выражается равенством S_o = cU_y в котором величина с характеризует жесткость связей.

Уравнение равновесия

М= j rd N_o

А с учетом записанных данных соотношений принимает вид:

Af=cwoJ г¹ dA.

А

Входящий сюда интеграл, который берется по всей площади расположения связей, представляет собой полярный момент инерции J этой площади относительно центра вращения. Тем самым М = cWJ , откуда:

(Ю)

Для прямоугольной площади со сторона* ми b и h полярный момент инерции равен:

J^-tf1*»1).

Первоначальную интенсивность распределенной нагрузки находим согласно ранее записанному равенству So = CUW в которое подставляем Uo = rWy Получаем Sy = CU/Qr. В свою очередь, используя формулу (10) для первоначального угла поворота, будем иметь:

М

Далее действуем по аналогии с расчетом для дискретных связей (что, по сути, сводится к замене дискретного суммирования интегрированием).

Прибегая к линейной теории ползучести, записываем формулу:

Ш_о (0 = и_й + - J к (т)£ (т ^k, (12) ^с о

Здесь г — текущее время, причем 0 < т < L

Перемещения (сдвиги) пропорциональны расстояниям от центра в любой момент времени, поэтому U 0) = rW UY U_Q - rW_w В первом из этих равенств U^ (/) означает угол поворота в момент времени L Подстановка выражений U (/) и U_Q в (12) дает:

rw(l) - rw₀+-j к (т )S (т )т,   (13)

Умножаем обе части этого равенства на и получаем:

?w (0 = г W_O+ - f к (т )г£ (т )dt.

со

Интегрирование по всей площади дает:

О L-* J

Но р5(т>Ы = Л/, поэтому, принимая во внимание (10), приходим к формуле:

W(i)-W₆ X+^kU^dT .     (14)

L о J

Получаем уравнение ползучести при распределенных связях, идентичное уравнению (8), которое описывает ползучесть при дискретных связях. Продифференцировав (13) по t, будем иметь:

dw (t)    1 , . . „ . .

г—7"”t U)S(O- d с, ,^(О

Поскольку согласно (14)——— = w₀£(c), получаем равенство crw_Q = s UY

Учитывая, что crw₀ = s₀, приходим к равенству:

S (О = So. (15)

Это означает, что интенсивность сдвигающих усилий во всех точках соединения инвариантна относительно времени.

В целом можно констатировать, что для обеих разновидностей связей (дискретных и равномерно распределенных) справедливо одно и то же уравнение ползучести, выражаемое формулами (8) и (14), а распределение передаваемых усилий не зависит от времени.

Поступила 16.09.08.