Об особенностях нелинейного взаимодействия поверхностной волны с гранями клиновидной пластины

Известно [1], что по своей структуре поверхностная волна Рэлея представляет неоднородную волну, в которой смещения затухают по мере удаления от поверхности, по которой распространяется волна. При этом пространственная структура и параметры волны в процессе движения остаются неизменными.

Распространение этой волны в клиновидной пластине имеет совершенно иной характер. При движении волны Рэлея по поверхности одной грани клина в направлении ребра при углах раствора q0 < 90° происходит изменение, как амплитуды, так и ее скорости.

Причина этого феномена кроется в том, что при движении волны изменяются условия распространения: смещения частиц вблизи одной грани клина в какой-то момент времени начинают достигать противоположной грани. Взаимодействие с поверхностью второй грани клина обуславливает расщепление движущейся волны на независимые поверхностную и объемную компоненты [2]. Энергия распространяющейся волны начинает уменьшаться, т.к. объемные волны, оттекающие с поверхности вглубь среды, уносят с собой часть энергии.

Также изменяется структура волны: при взаимодействии с поверхностями обеих граней клина происходит расщепление исходной волны Рэлея на независимые симметричную и антисимметричную моды.

Рассмотрим в рамках плосковолновой модели подход, позволяющий определить изменяющиеся в ходе движения параметры волны.

Малые возмущения, распространяющиеся вдоль поверхности и состоящие из продольных и поперечных компонент, можно найти из стандартных уравнений акустики

AUt + к2U( = 0, AUt + kt2Ut = 0. (1)

Введение продольного и поперечного потенциалов, связанных со смещениями продольных U , и поперечных U t волн соотношениями U , = grad Ф ,U _t = rot Ф и позволяющее перейти от векторных уравнений к скалярным, преобразует систему (1) к виду:

АФ + к 2 Ф = 0, АФ + к,2Ф = 0. (2)

В двумерной геометрии потенциалы зависят только от двух пространственных координат x , z и от времени t и решение (2) ищем в виде:

Ф = A exp ( ik _r x - i to t + iq _r z ) ,

Ф = Ap exp ( ik _r x - i to t + is _r z ) .

В выражениях (3) величины q r , s r _, имеющие смысл коэффициентов спада амплитуды смещений с удалением от границы, определяются равенствами:

qr = Vkr2 - k i , sr = Vkr2 - kt2 , а коэффициент p выражающий связь между потенциалами, соотношением:

P = -Ц/Qr / sr .

В этих формулах k t , k _t , k_r - соответственно волновые числа продольных, поперечных и искомых волн, to — круговая частота.

Амплитуда смещений А задается источником возбуждения и считается величиной известной, а определяемым параметром является волновое число k r . Для его нахождения дополнительно используются стандартные граничные условия [1].

В классическом случае скорость волны, определяемой из соотношения V = Ш / k r и начальная амплитуда смещений А являются величинами конечными и неизменными в ходе движения волны.

Для среды клиновидной формы ситуация совершенно другая. В ходе движения волны изменяются скорость и амплитуда смещений, зависимости которых от координат неизвестны, и решить уравнения (2) для функций ф и у не представляется возможным. Однако при медленном изменении этих величин в пределах локальной длины волны можно воспользоваться приближенными методами. На малых интервалах изменения x и t , решения общего вида можно рассматривать как состоящие из элементарных решений, зависимости которых имеют вид:

Ф(x) = A0 exp[ik(x)x - imt],

У( x) = A 0 p exp[ik (x) x -imt ].

Волновое число в этих соотношениях выражается в комплексном виде: k ( x ) = k ₁( x ) + ik ₂( x ) , где действительная часть этого числа характеризует скорость волны: V ( x ) = to / k ₁( x ) , а мнимая - амплитуду: A ( x ) = A ₀ exp [ - k ₂ ( x ) ] .

ПОСТАНОВКА ЗАДАЧИ

Решения (4) целесообразно искать в виде комбинаций функции Ханкеля первого рода:

ф = [ A H (k

У= [ A H ’( k l P )sin(p 2 е ) + C 1 H ’( k l P )cos ^ /2 е )], (6) поскольку эти функции удовлетворяют условию погашения, т.е. обращаются в нуль при бесконечном значении комплексного аргумента.

В этих формулах n1, n2 – угловые волновые числа, которые предполагаем медленно изменяющимися на локальной длине волны.

Как известно [3], компоненты тензора напряжений в криволинейной системе координат имеют вид:

С ре

= * (-^+ р э е

Э U е _- U е ’

Э р   р

Uр, Э Uр, ¹ Э Uе Э Uz.. -Л Э Uе Uр..

С ее = ^ ⁽--⁺ "Г--⁺--— ⁺ -г—’ ^{+ 2} * ⁽--— ⁺--’.

р   Эр р Эе    э z      р Эе р

Если использовать связь смещений с потенциалами:

ЭФ 1 э у

U р =    ⁺--^, U е =

Э р р Э е

1 ЭФ Э у

^^^^^^в

р э е    э р ’

то соотношение (7) в терминах волновых потенциалов можно переписать в виде:

(2 д2Ф 2 дФ 1 ду 1 д2у ] се = р\-----— + — +——I.

^р ( р дрде р де р др р де² J .

Рис. 1. Система координат (U – п_r адающая волна )

Сее = 2Д

-

kil Ф

-

^Ф - д f дУ^ I др2   др( р де J

Подстановка выражений (6) в граничные условия (5) приводит к системе однородных алгебраических уравнений. С учетом соотношений для цилиндрических функций [4]:

2 v Z _v ( z ) = zZ _v -1 - zZ _v +1 , 2 z ; ( z ) = - Z _v -1 - Z _{v +}1 , определители полученной системы уравнений принимают компактный вид:

Рассмотрим теоретическую модель распространения волны Рэлея из бесконечности перпендикулярно к ребру клина. Для решения задачи воспользуемся цилиндрической системой координат (Рис.1), которая приводит уравнения (2) к виду:

H v +

^^^^^^B

kt2

k;

^^^^^^B

1 I H v , ( k _t р )

H ^- H v ₁

H ⁺

v г

v г

th v ₂ 6 th v ₁ 6

= 0,(10)

д 2Ф £ дФ др2 р др

1 д 2Ф

+ р2 де2

+ k ;ф = 0,

Я±           O’            O’ vj (xj ’ H vj-2 (xj ’ — Hvj+2(xj ’ , J = 1,2 ,

x1 = ktр, x2 = ktp, m = —1, и имеют смысл дисперсионных соотношений для симметричной (m = 1) и антисимметричной (m = –1) мод поверхностной волны. Штрихами в этих фор-

д2 У J д 1 д2 У др2 р др р2 де2

+ k_t ² У = 0 ,

и дополним стандартными граничными условиями, выражающими отсутствие напряжений на поверхностях клина:

° 99 = ° ре = 0, при 6 = —6 ₀ . (5)

мулах помечены производные цилиндрических функций по координате.

Для вычисления полученных комплексных дисперсионных уравнений для функций Ханкеля применим асимптотические выражения Лангера [4], которые для произвольного н >> 1 дают в интервале 0 <  Z < ^ равномерные представления:

. 2 1

H _v ^o)( z ) = 4 ёе '^TH (²⁾ ( i VtoA ),

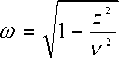
A = — Artn( to ) -1, to

и далее используя (11) и известную асимптотику Ханкеля [4]:

H ^; 2exp i(z-T-1) Jlz

окончательно получим:

H ,) ^{( k} , P ^{) =} J-r-^exP

^{V 1}           у л к р

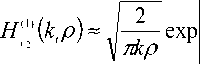
ikp - i v ₂ Artn

- ik p - i v ₁ Artn

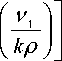
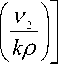
, (12)

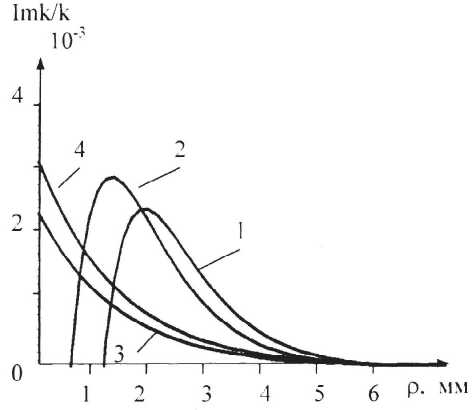
Рис. 3. Зависимость коэффициента затухания волны от расстояния до ребра для тех же углов клина

где связи волновых величин k, ^ , V между собой выглядят следующим образом

kr = д/v2 - к2 r2 = ^р2 - kt2 r2 .

Расчет показал, что решение этой задачи существует только при комплексных значениях вектора k . Следовательно, для удовлетворения условия отсутствия напряжений на поверхностях граней клина, волновой вектор k должен принимать комплексные значения, что соответствует физическим представлениям. В предельном случае р ^ ^ получается асимптотическое решение Рэлея, согласующееся с экспериментальными наблюдениями.

Кривые дисперсии фазовой скорости, рассчитанные по формуле (10), представлены на рис. 2. Отметим особый характер пространственных зависимостей скоростей этих мод. С приближением к ребру до точки rсл имеем устойчивое стационар-

ное распространение поверхностной волны, а после этой точки происходит потеря устойчивости, сопровождающаяся возникновением двух мод. При этом оказывается, что скорости распространения этих мод при приближении к ребру будут изменяться различным образом. Скорость симметричной моды стремится к скорости продольной волны, а антисимметричной – к нулю. Схожая картина наблюдается в плоскопараллельной пластине при монотонно уменьшающейся толщине [1]. Волновой вектор выражается в комплексном виде, состоящий из двух слагаемых: к = к ₁ + ik 2 . Сомножитель exp ( - k₂р ) в соотношении (12) определяет затухание волн, монотонно возрастающее с приближением к ребру (рис. 3).

Рассмотренные особенности возникают в области, протяженность которой очень резко зависит угла раствора клина (рис. 4). Так, например, при изменении угла от 5° до 25° эта область сокращается в 10 раз.

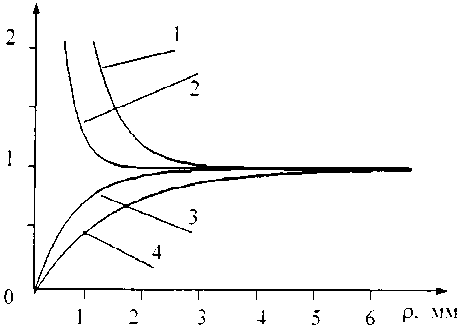
Рис. 2. Зависимость относительной скорости волны от расстояния до ребра для симметричных (1 и 2) и антисимметричных (3 и 4) углов клина: 1 и 3 - для 0 0 = 3°; 2 и 4 - для 0 0 = 5°

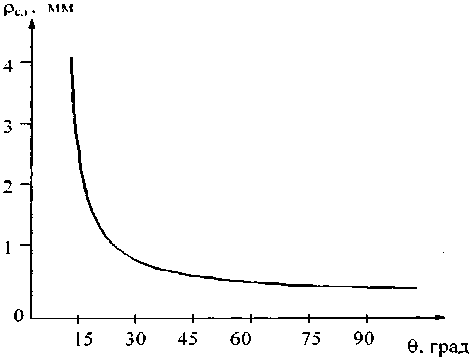
Рис. 4. Зависимость протяженности области “неустойчивого распространения” волны от угла клина

Таким образом, анализ акустических характеристик поверхностной волны в клине, проведенной в рамках классического подхода, приводит к выводу о том, что исследования выявили особый тип поверхностных волн, сопровождающийся в ходе движения непрерывной перестройкой акустического поля. Отметим также, что представленная модель позволяет понять физические процессы, происходящие при распространении поверхностной волны в остроугольном клине.