Об управлении группой объектов как о задаче системного анализа

Введение. Моделирование многомерных безынерционных объектов продолжает оставаться актуальной задачей идентификации. При этом основной упор настоящей статьи делается на случай, когда вектор компонент выходных переменных стохастически зависим заранее неизвестным образом. В этом случае подход к моделированию подобных объектов не укладывается в рамках существующей теории идентификации. Примеров подобных объектов в действительности предостаточно. В частности, к ним могут быть отнесены процессы, возникающие в стройиндустрии (производство цемента), металлургии (процесс плавки стали), энергетике (процесс горения угля), нефтепереработке (процесс очистки дизельного топлива от сернистых соединений), а также практически во всех организационных процессах, включающих в себя образовательный [1; 2]. Можно привести в пример многомерный процесс на нефтеперерабатывающем заводе, где существует установка гидроочистки дизельного топлива от сернистых соединений, совмещенная с процессом гидродепарафинизации, повышения хладотекучести дизельного топлива [3]. Измерение основных выходных стохастически зависимых переменных данного процесса, например, таких как «плотность при температуре 15 ^оС» или «температура конца кипения», происходит один раз в сутки. При этом исследуемый процесс рассматривается как безынерционный с запаздыванием [4].

Следует заметить, что любому из этих процессов соответствует постановка отличающихся формулировок задач и это отличие обусловлено наличием различных априорных сведений об изучаемом процессе. Наиболее интересным является случай, когда характер стохастической связи между компонентами выхода оказывается неизвестным с точностью до параметров. На рис. 1 представлена наиболее простая схема последовательно соединенных объектов. Тем не менее, даже она показывает, что при анализе такой группы объектов возникает специфика и при моделировании и тем более при управлении подобным процессам в действительности.

Рис. 1. Группа объектов, реализующих технологический процесс

• Fig. 1. The group of objects that implement a technological process

На рис. 1 приняты следующие обозначения: O, q = 1, r - количество объектов (технологических аппаратов), входящих в группу (группа состоит из локальных объектов); u = U, u ₂,..., u_m ) - входные управляющие воздействия; ц = ( ц , ц ,..., ц ) - входные, неуправляемые, но контролируемые переменные (например, это могут быть всевозможные добавки, при работе с сыпучими материалами, которые поступают на вход объекта); x = ( x , x ₂,..., x_n ) - характеристики, определяющие состав исходного продукта х₁ полуфабрикатов x ,..., x ; z – параметры, характеризующие готовый продукт (изделие). Все переменные – векторы. Протекание технологического процесса подчинено технологическому регламенту (ГОСТам), который определяет диапазоны значений всех технологических параметров.

Основная особенность, возникающая у группы процессов, в значительной степени обусловлена ее эмерджентностью [5] и неоправданно большими диапазонами технологического регламента. Причем сжатие технологического регламента на реальном производстве в большинстве случаев осуществить нельзя из-за возникающих организационных проблем. А в итоге это приводит, к сожалению, к выпуску некачественных изделий, а зачастую и к большой доли брака. Трудности еще усугубляются тем, что не всегда получившиеся изделия можно отправить на повторную переработку. Выход может быть найден на пути коррекции технологического регламента в каждом конкретном случае. Это, естественно, приводит к проблеме автоматизации подобного процесса в каждом локальном случае, на каждом переделе технологического процесса. В этой связи необходимо задачу идентификации и задачу управления решать для каждого технологического объекта, а уже потом объединять их в группу. Таким образом, возникает необходимость вести технологический процесс все время по-разному. Это сродни известной мысли, высказанной польским философом Фердинанда-Бронислава Трентовским в 1843 г. в книге «Отношение философии к кибернетике как к искусству управления народом»: «Применение искусства управления без сколько-нибудь серьезного изучения соответствующей теории подобно врачеванию без сколько-нибудь глубокого понимания медицинской науки».

Он подчеркивал, что действительно эффективное управление должно учитывать все важнейшие внешние и внутренние факторы, влияющие на объект управления: «При одной и той же политической идеологии кибернет должен управлять различно в Австрии, России или Пруссии. Точно так же и в одной и той же стране он должен управлять завтра иначе, чем сегодня».

В таких сложных многомерных процессах выходные переменные объекта каким-то образом зависимы, но зависимость эта априори оказывается неизвестной. Подобные процессы были названы Т-процессами, а их модели – Т-моделями [6]. Идентификация и управление такими процессами должны осуществляться не традиционным путем [7], так как он не приведет к успеху из-за недостатка априорной информации об исследуемом объекте. Особенностью является то, что вектор выходных компонент, обозначим его как x(t) = (x(t),x2(t),...,xn(t)), j = 1,n, таков, что компоненты этого вектора зависимы заранее неизвестным образом. Поэтому математическое описание объекта можно представить в виде системы неявных функций:

F j ( u ( t ) , ц ( t ) , x ( t )) = 0, j = 1, n ,

где    u ( t ) = ( u ( t ), u₂( t ), ..., u_m( t )), k = 1, m - вектор входных управляемых компонент;

(ц(t), ц(t),..., ц (t)) v = 1,p - вектор входных неуправляемых, но контролируемых компонент; компонента (t) - означает рассмотрение входных-выходных переменных в конкретный момент времени t. Задача идентификации рассматриваемых объектов сводится к тому, что необходимо решить систему неявных нелинейных уравнений (1) относительно компонент вектора выходных переменных x(t) при известных входных u(t),ц(t). Конечно, задача усложняется при наличии группы объектов, где каждый локальный объект придется рассматривать по отдельности.

Управление такими объектами рассматривается в условиях неопределенности, когда нет описание объекта с точностью до вектора параметров. Причем для группы объектов задающие воздействия для каждого отдельного объекта придется изменять.

Алгоритмы идентификации локальных объектов. Для моделирования группы объектов необходимым этапом является построение моделей самих локальных объектов. В этом случае необходимым будет рассмотрение известных методов, в частности, алгоритмов идентификации в узком и широком смыслах. Далее рассмотрим основные алгоритмы моделирования локальных объектов. Выделим два класса идентификации - параметрическая и непараметрическая.

Рассмотрим параметрическую идентификацию или идентификацию в узком смысле [8]. При идентификации в узком смысле рассматриваются обычно два основных этапа. Первый -определение параметрической структуры объекта с точностью до коэффициентов, второй -определение значений коэффициентов по результатам измерений входных-выходных переменных или оценки параметров. Чаще всего в различных источниках рассматриваются алгоритмы оценки параметров. Наиболее уязвимым этапом является выбор структуры модели объекта с точностью до коэффициентов. Совершенно ясно, что если структура модели выбрана неточно, то это приведет и к неточности модели. Здесь уместно вспомнить фразу древнегреческого философа Демокрита: «Даже незначительное отступление от истины в дальнейшем ведет к бесконечным ошибкам».

Таким образом, на первом этапе выбирается класс уравнений:

F(u,ц,x,а) = 0, j = 1,n, где u - входные управляемые переменные процесса, ц - входные неуправляемые, но контролируемые переменные процесса, x - выходные переменные, а - вектор параметров.

Алгоритмы оценки параметров основаны на методе стохастических аппроксимаций, в частности имеют следующий вид:

a k = a^k _{s - 1} + Y s x_s

s

N

\

k

Z ^a S И ' к ) Г ⁽ u t ) .

i = 1

Подобных алгоритмов известно много, но на этом подробно останавливаться не будем.

В случае непараметрической идентификации или идентификации в широком смысле алгоритмы простых постановок задач могут быть основаны на непараметрических оценках функции регрессии Надарая-Ватсона [9]. Для многомерного случая вид этой оценки представляется в следующем виде:

s

m

Z хП Ф

uk

—

uki

x s ⁽ u ) =

i = 1

k = 1

V

cs

sm

ZO Ф

i = 1 k = 1

u k

—

uki

V

cs

где колоколообразные функции Ф ( • ) и параметры размытости e_s удовлетворяют некоторым

условиям сходимости и удовлетворяют следующим свойствам [9]:

c s ¹ f ^Ф ( с s ¹ ( u k - u^Vu = 1;

Q ( u )

lim c Ф s ^^

^{( c}s '( u k

- ^uki ) ) = ^ ( ^uk - u ki ) ^;

0 <  Ф ^{( c}s 1 u_t - u k^ ^ ;

c_s >  0;      lim c s = 0;

s ^M

lim sc m = to .

s ^TO

На практике чаще всего встречаются случаи, когда векторы выходных переменных объекта стохастически зависимы. В этом случае описание процесса может быть представлено в виде:

Fj ( u, ц , x ) = 0, j = 1, n .

А модель объекта в этом случае, на основе аппроксимации локального типа, может быть представлена следующим образом:

F j ( u, ц , x, U s , M s , X s ) = 0, j = 1, n, i = 1, s ,

где u_s , ц , x_s - временные вектора (набор данных, поступивший к s-му моменту времени). Причем функции / ^(•) неизвестны, так как неизвестны зависимости выходных переменных процесса. Как было отмечено выше, процессы, имеющие стохастическую зависимость выходных переменных, были названы Т-процессами.

Рассмотрим каждый отдельный объект, входящий в группу, как отдельный многомерный объект с зависимостями входных и выходных переменных, а также неизвестными зависимостями выходных переменных между собой. Изобразим такой объект на рис. 2.

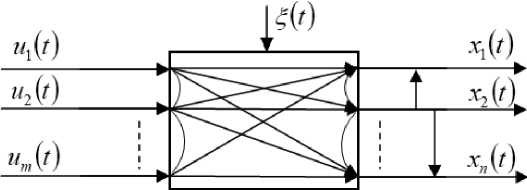
Рис. 2. Многомерный объект

Fig. 2. Multidimensional object

На рис. 2 на вход объекта поступает вектор входных переменных u = (ц,...,um ), на выходе наблюдается вектор выходных переменных x = (xv,...,xn),  §(t) - случайные помехи, действующие на объект. При рассмотрении такого объекта можно заметить зависимости выходных переменных, которые могут быть не всегда известны. По различным каналам многомерного Т-объекта зависимость j-ой компоненты вектора выходных переменных x может быть представлена в виде некоторой зависимости от тех или иных компонент вектора входных переменных u : x = f(u ), j = 1, n . Такие функции определяет исследователь из имеющейся априорной информации, и они называются составным вектором. Составной вектор – это вектор, составленный из некоторых компонент входных и выходных переменных, также это может быть любой набор, например x<2> = (u3, u6, x4), x<4> = (u2, u, u6, x3). По различным каналам многомерной системы может быть разное количество компонент u(t), входящих в составные вектора x(t).

Модель такого процесса рассматривается в виде системы:

j u < ^j > , x < ^j > ) = 0, j = In ,                              (6)

где функции F ( • ) продолжают оставаться неизвестными.

В результате измерений входных и выходных переменных объекта может быть получена обучающая выборка { u , x } , i = 1, 5 . В этом случае при заданных значениях входных переменных u ( t ) необходимо решить систему (6) относительно компонент выходных переменных x ( t ) . В результате можно получить оценки компонент выходных переменных по известным входным, а в этом и заключается основное назначение искомой модели.

Т-модели. Выше было отмечено, что если выходные переменные имеют неизвестные стохастические зависимости, то они были названы Т-объектами, а их модели Т-моделями. Описание такого процесса принимается в следующем виде:

F j ( u < j > ( t ) , x < j > ( t ) ) = 0, j = In ,                                    (7)

где u < j > ( t ), x < j > ( t ) - составные векторы, вид функции F _y( • ) неизвестен. Система моделей исследуемого объекта может быть представлена в следующем виде:

F j ( u < j > ( t ), x < j > ( t ), x , , u , ) = 0, j = 1, n ,                                 (8)

где x_s , u - временные векторы, но и в этом случае F ( • ) продолжают оставаться неизвестными. Поэтому задача сводится к тому, что при заданном значении вектора входных переменных u ( t ) необходимо решить систему (8) относительно вектора выходных переменных x ( t ) . Общая схема решения такой системы сводится к непараметрической двушаговой алгоритмической цепочки, которая позволяет найти прогнозные значения вектора выходных переменных x ( t ) по известным входным u ( t ) .

Сначала вычисляются невязки по формуле

_Е„= Fu < j * , x < j * ( i\x , , u , Ji j = 1, n ,                              (9)

где функции f ( u < ^j > , x < ^j > ( i ), :x_s , H_s ) принимаются в виде непараметрической оценки функции регрессии Надарая – Ватсона [9]:

s

< n >

^s J ^{( i} ) = fjjk u < ^J > , ^XJ ^{( i} ) ) = ^XJ ^{( i )— 221}

Z X j [ i ] П Ф

k = 1

s <  n >

i = 1 k = 1

^{Г u}k ^- u k ^[ i ^]

k     c ^suk

u k ^- u k ^[ i ^]

,

k     ^csu._t     7

где j = 1, n , , <  m >  - размерность составного вектора u_k . Колоколообразные функции

Ф ( • ) и

параметр размытости c удовлетворяют некоторым условиям следующими свойствами [9]:     Ф (;) <-/ ; lim^_Ю С = 0;

сходимости и обладают

J ^{Ф ( c -1} _t ^{( u} k ^- u k ^[ i ] ^{) ) du} = 1;

Q ( u )

lim „ c ¹ Ф ( c ¹ ( u ‘ — u, s —^^   su ^      su k    k     k

— u k [ i ^{] )} ; lim s _(/ sc s =да .

Далее оценивается условное математическое ожидание:

Xj = M { x | u < ^j > , s = o } , j = 1, n .

где за основу берется непараметрическая оценка функции регрессии. И в конечном итоге прогноз для каждой компоненты вектора выходной переменной будет находиться следующим образом:

s

< n >

Z -ФтП Ф

" u k 1

—

^ x ˆ j

i = 1

k 1 = 1

k c su

u_k [ i ] 1 < m > ^1-п ^Ф

7 k 2 = 1

Г = k , ^{[ i ]} 1

v c s s

s zn Ф i=1 k1 =1

^ u k 1

—

k      c su

uk ^[ i ^] 1 < m T

— п ^Ф

7 k 2 = 1

Г S k 2 ^[ i ^] 1

c k css  7

- , j = 1, n ,

где колоколообразные функции Ф ( • ) могут быть взяты в виде треугольного ядра для входов (13) и невязок (14):

Ф

^ ^Uk 1

—

Ф

Г f k x l i ] 1

« k , [ i ^] )

k   c s s  7

k     c su      7

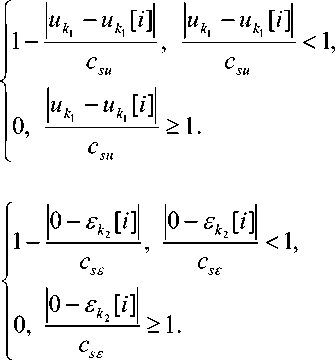
Непараметрический алгоритм (10) и (12) представляет собой двушаговую алгоритмическую цепочку, позволяющую находить прогнозные значения компонент вектора выхода при известных компонентах входных переменных, в случае стохастической зависимости выходных переменных [10].

Общая постановка задачи идентификации и управления группой объектов. Моделирование и управление группой объектов существенно отличается от моделирования и управления локальными объектами. И основное отличие состоит в том, что при управлении группой необходимо изменять задающие воздействия для управления локальными объектами, каждый раз изменяя при этом, по существу, технологический регламент. Этого требует реальность. Собственно, это и показывает приведенный ниже пример на нефтеперерабатывающем заводе. В противном случае технологическая карта требует расширения, но совершенно ясен результат исполнения этого расширенного технологического регламента, который неизбежно приведет к продукции низкого качества и даже к браку. Таким образом, цели, которые ставятся перед группой объектов, существенно отличаются от целей, которые ставятся перед локальными объектами. Остается еще раз заметить, что модели и алгоритмы управления не являются арифметической суммой моделей и алгоритмов группы объектов. Тем не менее, приведенные выше модели и алгоритмы управления могут быть приняты за основу. Изменится лишь содержание входных и выходных переменных локальных объектов и группы. Таким образом, для качественного управления группой необходимо отличие и в соответствующих технологических регламентах [11].

В конце 70-х гг. одному из авторов довелось участвовать в исследованиях технологического процесса по производству транзисторов (производственное объединение «Светлана», г. Ленинград), в связи с тем, что объем бракованных изделий и изделий низкого качества достигали 85 %. Проведенные исследования показали, что диапазоны значений технологических параметров неправдоподобно широки во всех сечениях технологического процесса, хотя и соответствовали технологическому регламенту. Результаты исследований позволили дать соответствующие рекомендации, которые вошли в отраслевые руководящие материалы [12].

Широкий диапазон значений характерен для многих добывающих или перерабатывающих производств. Конечно, можно разработать на основе исследований, проведенных для каждого конкретного предприятия, более жесткий технологический регламент и далее следовать ему. Но этот путь не всегда можно осуществить, потому как жесткий технологический регламент можно реализовать только на предприятиях с высоким уровнем культуры производства. Это, прежде всего, высокое качество технологического оборудования, средств локальной автоматики, квалификации работающих и их отношение к делу.

Может быть и другой путь, нужно следовать имеющемуся технологическому регламенту, но оптимизировать режим ведения процесса в данном технологическом объекте с учетом фактически проведенной технологической операции на предыдущем объекте. Такой путь более реалистичен для предприятий, так как не требует капитальных затрат на реконструкцию и позволяет существенно повысить качество выпускаемой продукции и уменьшить потери при производстве тех или иных изделий. Для этого необходимо разработать и внедрить компьютерные системы для улучшения технологических режимов. Подобные компьютерные системы оказываются достаточно эффективными.

Рассмотрим схему управления локальным объектом с запаздыванием (рис. 3).

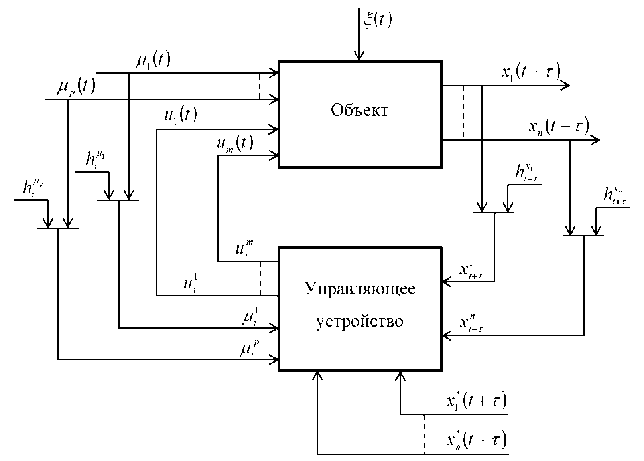
Рис. 3. Схема управления многомерным объектом

Fig. 3. Multidimensional Object Management Scheme

На рис. 3 приняты следующие обозначения: u(t) = (u[ (t),..., um (t)) — управляемые входные переменные;  M(t Ы^(t )v; M (t)) - неуправляемые, но контролируемые переменные;

x ( t + т ) = ( X ] ( t + т ) ,..., x_n ( t + т )) e R ⁿ

x * ( t + т ) = ( X ]* ( t + т ) ,..., x * ( t + т ) ) e R n

выходные     переменные     процесса;

задающие воздействия;  ^, hM, h  - случайные стационарные помехи, действующие на объект и в каналах измерения входных и выходных переменных; т - известное запаздывание по различным каналам многомерной системы.

Управление группой объектов должно осуществляться с учетом того, что переходя от одного объекта к другому необходимо изменять задающие воздействия.

Управление многомерными системами. Управление многомерными Т-объектами рассматривается в условиях непараметрической неопределенности, т. е. в условиях, когда модель процесса с точностью до вектора параметров отсутствует полностью [13]. В этом случае известные приемы не применимы и следует использовать другие подходы для решения задачи [14–18].

В задаче управления многомерным процессом со стохастической зависимостью выходных переменных используется многошаговая алгоритмическая цепочка. Она заключается в следующем: входная переменная u_x * ( t ) берется произвольно из области Q ( u _t) . Следующая входная переменная u * ( t ) находится в соответствии со следующим алгоритмом:

* u

s

Е ^u 2 Ф i = 1

* i

^ 1- ^ 1

к

c u

nx П Ф j = 1    к

*        i xj- xj

c

x j

< р >

П Ф

^V = 1 к

*

M v

-

^м 1

c v

s

Е Ф i=1

( u,

*

-

ui'

к

c_{u 1}

< n q >

П Ф

7 j = 1

v _x v _j

-

j

к

c

x j

< P w >  (

П Ф

V = 1    к

v i

M v^- M v

c

где < nq >, < pw > - размерность соответствующих составных векторов x им, < nq >< n, < pw >< p, q, w - количество компонент, входящих в составной вектор. Составные вектора определяются исследователем из имеющейся априорной информации. В случае если исследователь не располагает подобной информацией об объекте, он использует все компоненты входных и выходных переменных в составном векторе. Далее входная переменная и* (t) находится следующим образом:

s

*

*

u

Z иФ

i = 1

s

u

L

/

*

u

i

^U 2

< n q >

*

к

/

*

^cu 1

к

^cu 2

п Ф

7 j = 1

x j

—

xl

< Pw >

*

Z Ф

i = 1

u ₁

—

^u '

*

ф

u ₂

—

i u 2

< n q >

к

*

к

c_{u 1}

к

c_{u 2}

п Ф

7 j = 1

^cx j

п Ф

A v

^“

A )

x j

—

xj'

V = 1

к

c A v

< p_w >

/

*

.

к

c x_j

п Ф

V = 1

A v

—

A v

к

c A v

И далее алгоритм управления продолжается для нахождения каждой компоненты входа и * ( t ) объекта, причем с каждым последующим шагом в алгоритм добавляются вновь найденные на предыдущем шаге значения входных переменных. Запишем алгоритм управления для многомерной системы, который будет выглядеть следующим образом:

* u_k

5      к —1    7

Zuk п ф i=1      к=1

* i

^Uk ^{— U}k

<Х п ф j=1 к

*        i x x

x j

< P w >  п ф v = 1

*

A v

к

—

c A

A )

5  k ^—1    7

^п Ф i = 1 к = 1     к

* i

^Uk ^{— U}k

nnx п ф j=1 к

* _x * _j

—

xi'

c x_j

< P w >

п ф v=1 к

* i

A v- A v

к = 1, m .

В алгоритме управления (17) настраиваемыми параметрами остаются параметры размытости для входных и выходных переменных c , c и с , для них могут быть использованы следующие формулы:    cUt = ^u* — ui| + n ,    cx. = вx* — xi| + П    и cA = Ya”* — Alv I + П, где a, в и Y некоторые параметры большие 1, а параметр 0 < n < 1.

Следует обратить внимание на то, что выбор параметров размытости cUk , cx, и сА осуществляется на каждом такте управления. При этом если сначала определен c , то определение cx, и сА осуществляется с учетом этого факта. Очередность определения параметров размытости cUk, cx, и сА несущественна.

Группа объектов на нефтеперерабатывающем заводе. На нефтеперерабатывающем заводе функционирует установка гидроочистки дизельного топлива от сернистых соединений, совмещенная с процессом гидродепарафинизации, повышения хладотекучести дизельного топлива. Представим технологическую схему рассматриваемого процесса (рис. 4).

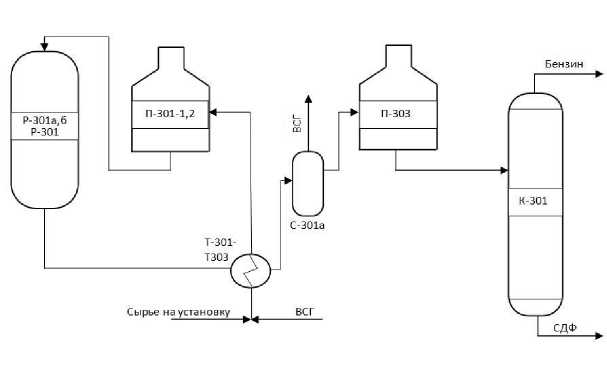
Рис. 4. Фрагмент схемы гидроочистки дизельного топлива и гидродепарафинизации Fig. 4. Fragment of a scheme for hydrotreating diesel fuel and hydrodewaxing

На рис. 4 представлен реакторный блок Р-301, в котором совмещены процессы гидроочистки и гидродепарафинизации, а также изображены блоки очистки циркуляционного водородсодержащего газа С-301а; стабилизации дизельного топлива с извлечением бокового погона К-301; стабилизации отгона бензина; очистки углеводородных газов. Входом является «Сырье на установку», а выходом «СДФ».

Изображенные блоки представляют собой группу объектов, при помощи которых происходят совмещенные процессы гидроочистки и гидродепарафинизации.

В процессе работы такой установки происходит сбор и накопление информации о протекании технологического процесса. Поэтому необходимо обрабатывать накопленную информацию с целью мониторинга за всем процессом и последующего принятия решений по его управлению [19].

Из-за недостатка априорной информации о процессе в нужном объеме для осуществления его моделирования и управления предлагается использовать методы непараметрических систем, которые помогут в определении текущего состояния технологических потоков на входе и выходе процесса, выявлении недостоверных данных, прогнозировании показателей качества готовой продукции на выходе, корректном управлении технологическим процессом.

Изобразим общую схему идентификации процессов гидроочистки и гидродепарафинизации в следующем виде (рис. 5).

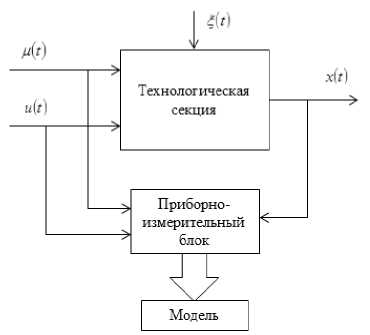
Рис. 5. Фрагмент моделирования процессов гидроочистки и гидродепарафинизации Fig. 5. Fragment of modeling hydrotreating and hydrodewaxing processes

Для процесса гидроочистки и гидродепарафинизации использовались следующие входные и выходные переменные: u_x (t ) - плотность при 15 ^оС, кг/м³; фракционный состав, ^оС: и_г (t ) -температура начала кипения; u₃ ( t ) - температура выкипания 50 %; u₄ ( t ) - температура выкипания 96 %; u₅ ( t ) - температура конца кипения; u₆ ( t ) - давление на входе в Р-301, кгс/см²; u₇(t ) - температура входа в Р-301, ^оС; x_x ( t ) - плотность при 15 ^оС, кг/м³; фракционный состав, ^оС: x₂ ( t ) - температура начала кипения; x₃(t ) - температура выкипания 50 %; x₄ ( t ) - температура выкипания 96 %; x₅(t ) - температура конца кипения; x₆ ( t ) - температура помутнения.

В связи с тем, что характер зависимости входных и выходных переменных неизвестен, а также неизвестны зависимости выходных переменных между собой, то в дальнейшем используется двушаговый непараметрический алгоритм Т-модели (10) и (12), рассмотренный выше, для определения прогнозных значений компонент вектора выхода по известным компонентам входа.

Точность моделирования оценивалась по следующей формуле

s

El x ^- x s ⁽ u )    _

5 j =     ----------- , j = 1, n ,

El x- x = 1

где x_i - наблюдения на объекте; x s ( u ) - прогноз выхода объекта; X - среднее значение по каждой компоненте вектора x .

Для моделирования проводим процедуру скользящего экзамена. Настраиваемыми параметрами будут параметры размытости с и c , которые в данном случае возьмем равным 0,5 и 0,4 соответственно (значения были определены в результате многочисленных экспериментов с целью уменьшения квадратичной ошибки между выходом объекта и модели). Объем выборки s = 115. Приведем результаты по выходной переменной x₄ ( t ) -температура выкипания 96 % (рис. 6).

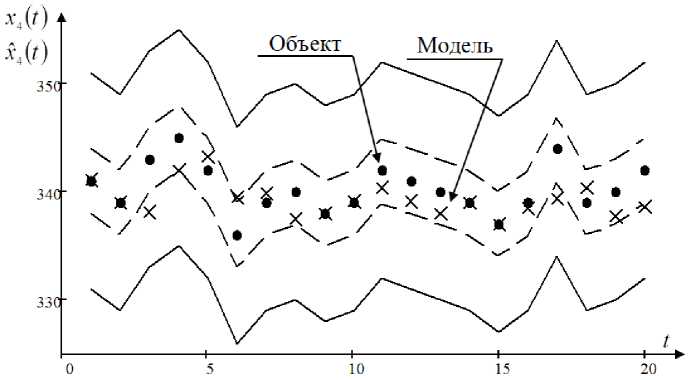
Рис. 6. Прогноз выходной компоненты x₄ (t )

при соответствующих входных

переменных u

( • )

Fig. 6. Prediction of the output component x ₄ ( t ) for the corresponding input variables u ( t )

На рис. 6 «точкой» обозначены выходы объекта, а «крестиком» выходы модели. Для наглядности представления результатов на графике показаны 20 точек выборки. Согласно ГОСТ Р 51069-97 Нефть и нефтепродукты. Метод определения плотности, относительной плотности и плотности в градусах API ареометром, показатели точности метода, полученные статистическим исследованием межлабораторных результатов испытаний, могут отклоняться, для x₄ ( t ) минимальное значение составляет - 3 0 С , как показано на рис. 6 пунктирными линиями, а максимальное значение составляет – 10 ⁰ С , как показано на рис. 6 сплошными линиями. Для каждой компоненты выхода объекта утверждены свои границы отклонений. Какие из границ выбрать, минимальные или максимальные, определяет технолог. По графику можно сказать, что получился вполне удовлетворительный прогноз, ошибка моделирования составила ^ = 0,04. Но стоит обратить внимание на то, что максимальные границы отклонений слишком широки во всех сечениях технологического процесса, и сам процесс должен проходить в минимальных границах отклонений. Получившиеся прогнозные значения иногда выходят за пределы минимальных границ, но лежат в пределах максимальных, на это могут влиять многие факторы, такие как малый объем обучающей выборки, недостоверность априорной информации, случайные помехи, действующие на процесс и т. д. Но хорошо настроенные модели позволяют повысить ее точность и в дальнейшем помогут для качественного управления технологическим процессом [20].

Заключение. В статье рассмотрены непараметрические алгоритмы моделирования и управления группой объектов в условиях как параметрической, так и непараметрической неопределенности. Создание групп обусловлено не только структурой предприятия, но и характером технологического процесса. Подчеркнута одна особенность, которая проявляется в том, что задающие воздействия для каждого объекта являются предметом специального рассмотрения на каждом такте управления. В работе приводятся модели и алгоритмы управления группой объектов, а также некоторых локальных и специально подчеркнуто свойство эмерджентности. Приведены модели многомерных безынерционных комплексов и рассмотрен, в частности, пример по результатам измерений реальных данных технологического совмещенного процесса гидроочистки и гидродепарафинизации дизельного топлива, происходящего на нефтеперерабатывающем заводе.